confidence and prediction intervals with StatsModels

Question

I do this linear regression with StatsModels:

import numpy as np
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std

n = 100

x = np.linspace(0, 10, n)
e = np.random.normal(size=n)
y = 1 + 0.5*x + 2*e
X = sm.add_constant(x)

re = sm.OLS(y, X).fit()
print(re.summary())

prstd, iv_l, iv_u = wls_prediction_std(re)

My questions are, iv_l and iv_u are the upper and lower confidence intervals or prediction intervals?

How I get others?

I need the confidence and prediction intervals for all points, to do a plot.

Solidus

https://mcmap.net/q/302463/-show-confidence-limits-and-prediction-limits-in-scatter-plot – Eladiaelaeoptene

Answer 1

update see the second answer which is more recent. Many of the models and results classes have now a get_prediction method that provides additional information including prediction intervals and/or confidence intervals for the predicted mean.

old answer:

iv_l and iv_u give you the limits of the prediction interval for each point.

Prediction interval is the confidence interval for an observation and includes the estimate of the error.

I think, confidence interval for the mean prediction is not yet available in statsmodels. (Actually, the confidence interval for the fitted values is hiding inside the summary_table of influence_outlier, but I need to verify this.)

Proper prediction methods for statsmodels are on the TODO list.

Addition

Confidence intervals are there for OLS but the access is a bit clumsy.

To be included after running your script:

from statsmodels.stats.outliers_influence import summary_table

st, data, ss2 = summary_table(re, alpha=0.05)

fittedvalues = data[:, 2]
predict_mean_se  = data[:, 3]
predict_mean_ci_low, predict_mean_ci_upp = data[:, 4:6].T
predict_ci_low, predict_ci_upp = data[:, 6:8].T

# Check we got the right things
print np.max(np.abs(re.fittedvalues - fittedvalues))
print np.max(np.abs(iv_l - predict_ci_low))
print np.max(np.abs(iv_u - predict_ci_upp))

plt.plot(x, y, 'o')
plt.plot(x, fittedvalues, '-', lw=2)
plt.plot(x, predict_ci_low, 'r--', lw=2)
plt.plot(x, predict_ci_upp, 'r--', lw=2)
plt.plot(x, predict_mean_ci_low, 'r--', lw=2)
plt.plot(x, predict_mean_ci_upp, 'r--', lw=2)
plt.show()

This should give the same results as SAS, http://jpktd.blogspot.ca/2012/01/nice-thing-about-seeing-zeros.html

Caddish

One issue with this method is that if the points are sparse, predict_mean_ci_low and predict_mean_ci_upp are going to be jagged/pointy when plotted because they only exist at the fitted values, instead of a range of points. However, the fit line is defined for all points. There is a comment that says using hat_matrix only works for fitted values in github.com/statsmodels/statsmodels/blob/master/statsmodels/… - any idea how to get around that? – Charley

I have an issue with the application of this answer to my dataset, posted as a separate question here: #34999272. Any advice much appreciated! – Aminaamine

This is an old question, but based on this answer, how would it be possible to only get those data points below the 95 CI? I posted this as new question #50586337 – Issuance

Isn't there a way to do the same when one does "fit_regularized()" instead? It seems that all methods work for normal "fit()" – Curfew

now C.I. is possible in OLS non-linear curve but linear in parameters¶ – Decry

Answer 2

For test data you can try to use the following.

predictions = result.get_prediction(out_of_sample_df)
predictions.summary_frame(alpha=0.05)

I found the summary_frame() method buried here and you can find the get_prediction() method here. You can change the significance level of the confidence interval and prediction interval by modifying the "alpha" parameter.

I am posting this here because this was the first post that comes up when looking for a solution for confidence & prediction intervals – even though this concerns itself with test data rather.

Here's a function to take a model, new data, and an arbitrary quantile, using this approach:

def ols_quantile(m, X, q):
  # m: OLS model.
  # X: X matrix.
  # q: Quantile.
  #
  # Set alpha based on q.
  a = q * 2
  if q > 0.5:
    a = 2 * (1 - q)
  predictions = m.get_prediction(X)
  frame = predictions.summary_frame(alpha=a)
  if q > 0.5:
    return frame.obs_ci_upper
  return frame.obs_ci_lower

Mera

predictions.summary_frame(alpha=0.05) throws an error for me (TypeError: 'builtin_function_or_method' object is not iterable). I've raised an issue on github: github.com/statsmodels/statsmodels/issues/4437 – Cinda

What is out_of_sample_df? Or more generally, what parameters does get_prediction() take? When I try to feed it e.g. x-values for the prediction, it ValueErrors out. – Lullaby

@Lullaby See statsmodels.org/dev/generated/…. – Shriner

@Lullaby Check if you have added the constant value. – Myasthenia

Answer 3

With time series results, you get a much smoother plot using the get_forecast() method. An example of time series is below:

# Seasonal Arima Modeling, no exogenous variable
model = SARIMAX(train['MI'], order=(1,1,1), seasonal_order=(1,1,0,12), enforce_invertibility=True)

results = model.fit()

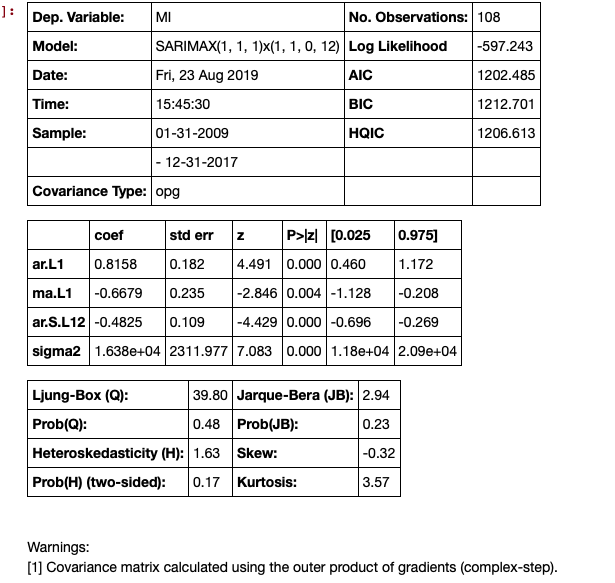
results.summary()

The next step is to make the predictions, this generates the confidence intervals.

# make the predictions for 11 steps ahead
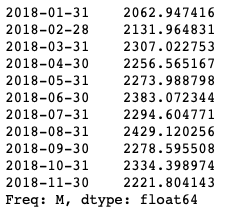
predictions_int = results.get_forecast(steps=11)
predictions_int.predicted_mean

These can be put in a data frame but need some cleaning up:

# get a better view
predictions_int.conf_int()

Concatenate the data frame, but clean up the headers

conf_df = pd.concat([test['MI'],predictions_int.predicted_mean, predictions_int.conf_int()], axis = 1)

conf_df.head()

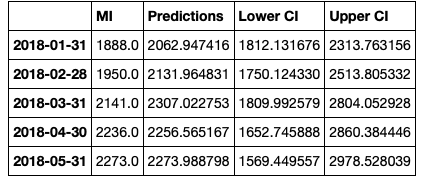
Then we rename the columns.

conf_df = conf_df.rename(columns={0: 'Predictions', 'lower MI': 'Lower CI', 'upper MI': 'Upper CI'})
conf_df.head()

Make the plot.

# make a plot of model fit
# color = 'skyblue'

fig = plt.figure(figsize = (16,8))
ax1 = fig.add_subplot(111)


x = conf_df.index.values


upper = conf_df['Upper CI']
lower = conf_df['Lower CI']

conf_df['MI'].plot(color = 'blue', label = 'Actual')
conf_df['Predictions'].plot(color = 'orange',label = 'Predicted' )
upper.plot(color = 'grey', label = 'Upper CI')
lower.plot(color = 'grey', label = 'Lower CI')

# plot the legend for the first plot
plt.legend(loc = 'lower left', fontsize = 12)


# fill between the conf intervals
plt.fill_between(x, lower, upper, color='grey', alpha='0.2')

plt.ylim(1000,3500)

plt.show()

Cornstarch

Answer 4

You can get the prediction intervals by using LRPI() class from the Ipython notebook in my repo (https://github.com/shahejokarian/regression-prediction-interval).

You need to set the t value to get the desired confidence interval for the prediction values, otherwise the default is 95% conf. interval.

The LRPI class uses sklearn.linear_model's LinearRegression , numpy and pandas libraries.

There is an example shown in the notebook too.

Wheatley

Answer 5

summary_frame and summary_table work well when you need exact results for a single quantile, but don't vectorize well. This will provide a normal approximation of the prediction interval (not confidence interval) and works for a vector of quantiles:

def ols_quantile(m, X, q):
  # m: Statsmodels OLS model.
  # X: X matrix of data to predict.
  # q: Quantile.
  #
  from scipy.stats import norm
  mean_pred = m.predict(X)
  se = np.sqrt(m.scale)
  return mean_pred + norm.ppf(q) * se

Genteel

Answer 6

To add to Max Ghenis' response here - you can use .get_prediction() to generate confidence intervals, not just prediction intervals, by using .conf_int() after.

predictions = result.get_prediction(out_of_sample_df)
predictions.conf_int(alpha = 0.05)

Egis

Answer 7

You can calculate them based on results given by statsmodel and the normality assumptions.

Here is an example for OLS and CI for the mean value:

import statsmodels.api as sm
import numpy as np
from scipy import stats

#Significance level:
sl = 0.05
#Evaluate mean value at a required point x0. Here, at the point (0.0,2.0) for N_model=2:
x0 = np.asarray([1.0, 0.0, 2.0])# If you have no constant in your model, remove the first 1.0. For more dimensions, add the desired values.

#Get an OLS model based on output y and the prepared vector X (as in your notation):
model = sm.OLS(endog = y, exog = X )
results = model.fit()
#Get two-tailed t-values:
(t_minus, t_plus) = stats.t.interval(alpha = (1.0 - sl), df =  len(results.resid) - len(x0) )
y_value_at_x0 = np.dot(results.params, x0)
lower_bound = y_value_at_x0 + t_minus*np.sqrt(results.mse_resid*( np.dot(np.dot(x0.T,results.normalized_cov_params),x0) ))
upper_bound = y_value_at_x0 +  t_plus*np.sqrt(results.mse_resid*( np.dot(np.dot(x0.T,results.normalized_cov_params),x0) ))

You can wrap a nice function around this with input results, point x0 and significance level sl.

I am unsure now if you can use this for WLS() since there are extra things happening there.

Ref: Ch3 in [D.C. Montgomery and E.A. Peck. “Introduction to Linear Regression Analysis.” 4th. Ed., Wiley, 1992].

Depressomotor