Show confidence limits and prediction limits in scatter plot

Question

I have two arrays of data for height and weight:

import numpy as np, matplotlib.pyplot as plt

heights = np.array([50,52,53,54,58,60,62,64,66,67,68,70,72,74,76,55,50,45,65])
weights = np.array([25,50,55,75,80,85,50,65,85,55,45,45,50,75,95,65,50,40,45])

plt.plot(heights,weights,'bo')
plt.show()

How can I produce a plot similar to the following?

Grasp

Answer 1

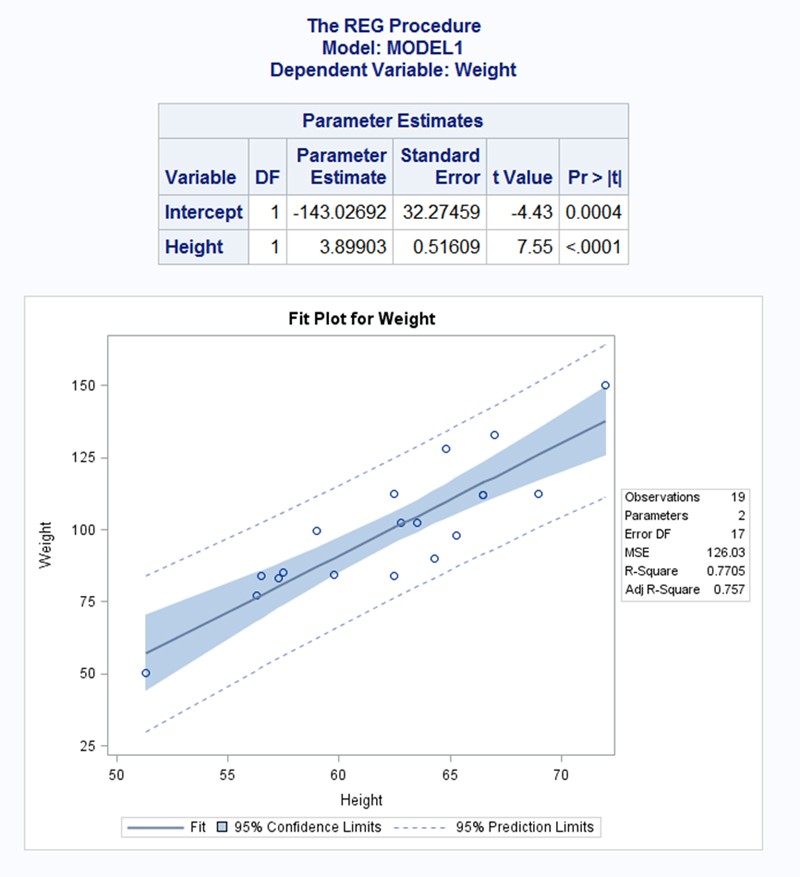
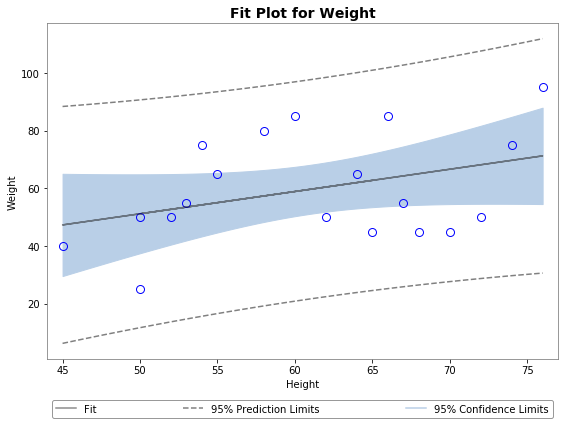
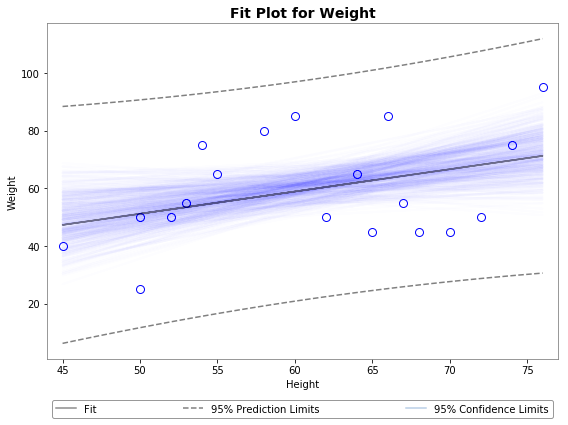
Here's what I put together. I tried to closely emulate your screenshot.

Given

import numpy as np
import scipy as sp
import scipy.stats as stats
import matplotlib.pyplot as plt


%matplotlib inline

# Raw Data
heights = np.array([50,52,53,54,58,60,62,64,66,67,68,70,72,74,76,55,50,45,65])
weights = np.array([25,50,55,75,80,85,50,65,85,55,45,45,50,75,95,65,50,40,45])

Two detailed options to plot confidence intervals:

def plot_ci_manual(t, s_err, n, x, x2, y2, ax=None):
    """Return an axes of confidence bands using a simple approach.
    
    Notes
    -----
    .. math:: \left| \: \hat{\mu}_{y|x0} - \mu_{y|x0} \: \right| \; \leq \; T_{n-2}^{.975} \; \hat{\sigma} \; \sqrt{\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum_{i=1}^n{(x_i-\bar{x})^2}}}
    .. math:: \hat{\sigma} = \sqrt{\sum_{i=1}^n{\frac{(y_i-\hat{y})^2}{n-2}}}
    
    References
    ----------
    .. [1] M. Duarte.  "Curve fitting," Jupyter Notebook.
       http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/CurveFitting.ipynb
    
    """
    if ax is None:
        ax = plt.gca()
    
    ci = t * s_err * np.sqrt(1/n + (x2 - np.mean(x))**2 / np.sum((x - np.mean(x))**2))
    ax.fill_between(x2, y2 + ci, y2 - ci, color="#b9cfe7", edgecolor="")

    return ax


def plot_ci_bootstrap(xs, ys, resid, nboot=500, ax=None):
    """Return an axes of confidence bands using a bootstrap approach.

    Notes
    -----
    The bootstrap approach iteratively resampling residuals.
    It plots `nboot` number of straight lines and outlines the shape of a band.
    The density of overlapping lines indicates improved confidence.

    Returns
    -------
    ax : axes
        - Cluster of lines
        - Upper and Lower bounds (high and low) (optional)  Note: sensitive to outliers

    References
    ----------
    .. [1] J. Stults. "Visualizing Confidence Intervals", Various Consequences.
       http://www.variousconsequences.com/2010/02/visualizing-confidence-intervals.html

    """ 
    if ax is None:
        ax = plt.gca()

    bootindex = sp.random.randint

    for _ in range(nboot):
        resamp_resid = resid[bootindex(0, len(resid) - 1, len(resid))]
        # Make coeffs of for polys
        pc = sp.polyfit(xs, ys + resamp_resid, 1)                   
        # Plot bootstrap cluster
        ax.plot(xs, sp.polyval(pc, xs), "b-", linewidth=2, alpha=3.0 / float(nboot))

    return ax

Code

# Computations ----------------------------------------------------------------    
# Modeling with Numpy
def equation(a, b):
    """Return a 1D polynomial."""
    return np.polyval(a, b) 


x = heights
y = weights
p, cov = np.polyfit(x, y, 1, cov=True)                     # parameters and covariance from of the fit of 1-D polynom.
y_model = equation(p, x)                                   # model using the fit parameters; NOTE: parameters here are coefficients

# Statistics
n = weights.size                                           # number of observations
m = p.size                                                 # number of parameters
dof = n - m                                                # degrees of freedom
t = stats.t.ppf(0.975, n - m)                              # t-statistic; used for CI and PI bands

# Estimates of Error in Data/Model
resid = y - y_model                                        # residuals; diff. actual data from predicted values
chi2 = np.sum((resid / y_model)**2)                        # chi-squared; estimates error in data
chi2_red = chi2 / dof                                      # reduced chi-squared; measures goodness of fit
s_err = np.sqrt(np.sum(resid**2) / dof)                    # standard deviation of the error

# Plotting --------------------------------------------------------------------
fig, ax = plt.subplots(figsize=(8, 6))

# Data
ax.plot(
    x, y, "o", color="#b9cfe7", markersize=8, 
    markeredgewidth=1, markeredgecolor="b", markerfacecolor="None"
)

# Fit
ax.plot(x, y_model, "-", color="0.1", linewidth=1.5, alpha=0.5, label="Fit")  

x2 = np.linspace(np.min(x), np.max(x), 100)
y2 = equation(p, x2)

# Confidence Interval (select one)
plot_ci_manual(t, s_err, n, x, x2, y2, ax=ax)
#plot_ci_bootstrap(x, y, resid, ax=ax)
   
# Prediction Interval
pi = t * s_err * np.sqrt(1 + 1/n + (x2 - np.mean(x))**2 / np.sum((x - np.mean(x))**2))   
ax.fill_between(x2, y2 + pi, y2 - pi, color="None", linestyle="--")
ax.plot(x2, y2 - pi, "--", color="0.5", label="95% Prediction Limits")
ax.plot(x2, y2 + pi, "--", color="0.5")

#plt.show()

The following modifications are optional, originally implemented to mimic the OP's desired result.

# Figure Modifications --------------------------------------------------------
# Borders
ax.spines["top"].set_color("0.5")
ax.spines["bottom"].set_color("0.5")
ax.spines["left"].set_color("0.5")
ax.spines["right"].set_color("0.5")
ax.get_xaxis().set_tick_params(direction="out")
ax.get_yaxis().set_tick_params(direction="out")
ax.xaxis.tick_bottom()
ax.yaxis.tick_left() 

# Labels
plt.title("Fit Plot for Weight", fontsize="14", fontweight="bold")
plt.xlabel("Height")
plt.ylabel("Weight")
plt.xlim(np.min(x) - 1, np.max(x) + 1)

# Custom legend
handles, labels = ax.get_legend_handles_labels()
display = (0, 1)
anyArtist = plt.Line2D((0, 1), (0, 0), color="#b9cfe7")    # create custom artists
legend = plt.legend(
    [handle for i, handle in enumerate(handles) if i in display] + [anyArtist],
    [label for i, label in enumerate(labels) if i in display] + ["95% Confidence Limits"],
    loc=9, bbox_to_anchor=(0, -0.21, 1., 0.102), ncol=3, mode="expand"
)  
frame = legend.get_frame().set_edgecolor("0.5")

# Save Figure
plt.tight_layout()
plt.savefig("filename.png", bbox_extra_artists=(legend,), bbox_inches="tight")

plt.show()

Output

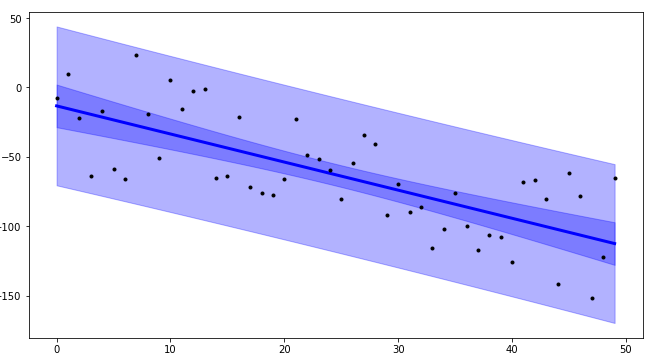
Using plot_ci_manual():

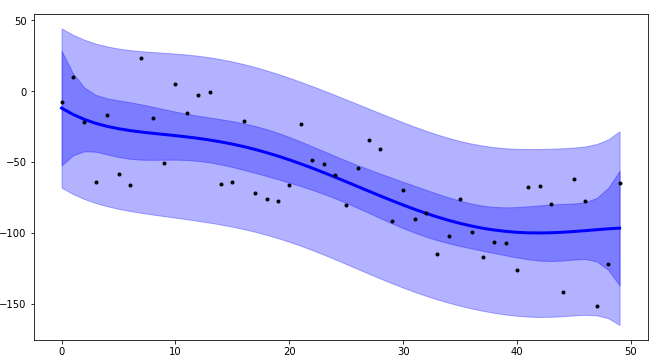
Using plot_ci_bootstrap():

Hope this helps. Cheers.

---

Details

1. I believe that since the legend is outside the figure, it does not show up in matplotblib's popup window. It works fine in Jupyter using %maplotlib inline.

2. The primary confidence interval code (plot_ci_manual()) is adapted from another source producing a plot similar to the OP. You can select a more advanced technique called residual bootstrapping by uncommenting the second option plot_ci_bootstrap().

Updates

1. This post has been updated with revised code compatible with Python 3.
2. stats.t.ppf() accepts the lower tail probability. According to the following resources, t = sp.stats.t.ppf(0.95, n - m) was corrected to t = sp.stats.t.ppf(0.975, n - m) to reflect a two-sided 95% t-statistic (or one-sided 97.5% t-statistic).
   • original notebook and equation
   • statistics reference (thanks @Bonlenfum and @tryptofan)
   • verified t-value given dof=17
3. y2 was updated to respond more flexibly with a given model (@regeneration).
4. An abstracted equation function was added to wrap the model function. Non-linear regressions are possible although not demonstrated. Amend appropriate variables as needed (thanks @PJW).

See Also

• This post on plotting bands with statsmodels library.
• This tutorial on plotting bands and computing confidence intervals with uncertainties library (install with caution in a separate environment).

Testudo

How would I modify this for a 2nd-order polynomial fit? The existing method only plots straight lines for the prediction limits. – Bullock

...still plots the prediction limits as straight lines... I also am having trouble using this method with repeated (x,y) pair entries. If you have any feedback on my related post it would be much appreciated! :#34999272 – Bullock

....the PIs and CIs produced by statsmodels are nonlinear. (note that the polynomial fits are still a linear equation). See my link above. Unfortunately the underlying equations are hidden in a bit of a black box with Statsmodels and seems to be breaking with my particular dataset. Thanks for the feedback! – Bullock

I had problems with the calculation of y2, as when the regression line is decreasing, the confidence iterval did not. With the present calculation of y2, the prediction y_model will always span from min to max. Therefore I changed the calculation of y2 to: y2 = np.linspace(y_model[x.index(np.min(x))], y_model[x.index(np.max(x))], 100) – Purnell

I see you have used the t-distribution for the distribution of both $E[Y|X]$ and $\hat{y}$. What justification do we have for that? – Homestead

Answer 2

You can use seaborn plotting library to create plots as you want.

In [18]: import seaborn as sns

In [19]: heights = np.array([50,52,53,54,58,60,62,64,66,67, 68,70,72,74,76,55,50,45,65])
    ...: weights = np.array([25,50,55,75,80,85,50,65,85,55,45,45,50,75,95,65,50,40,45])
    ...: 

In [20]: sns.regplot(heights,weights, color ='blue')
Out[20]: <matplotlib.axes.AxesSubplot at 0x13644f60>

Angeli

This only does half the job, but it does as a one-liner, so it's eminently worth having. – Ambrogio

Answer 3

I need to do this sort of plot occasionally... this was my first time doing it with Python/Jupyter, and this post helps me a lot, especially the detailed Pylang answer.

I know there are 'easier' ways to get there, but I think this way is much more didactic and allows me to learn step by step what's going on. I even learned here that there are 'prediction intervals'! Thanks.

Below is the Pylang code in a more straightforward fashion, including the calculation of Pearson's correlation (and so the r2) and the mean square error (MSE). Of course, the final plot (!) must be adapted for every dataset...

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

heights = np.array([50,52,53,54,58,60,62,64,66,67,68,70,72,74,76,55,50,45,65])
weights = np.array([25,50,55,75,80,85,50,65,85,55,45,45,50,75,95,65,50,40,45])

x = heights
y = weights

slope, intercept = np.polyfit(x, y, 1)  # linear model adjustment

y_model = np.polyval([slope, intercept], x)   # modeling...

x_mean = np.mean(x)
y_mean = np.mean(y)
n = x.size                        # number of samples
m = 2                             # number of parameters
dof = n - m                       # degrees of freedom
t = stats.t.ppf(0.975, dof)       # Students statistic of interval confidence

residual = y - y_model

std_error = (np.sum(residual**2) / dof)**.5   # Standard deviation of the error

# calculating the r2
# https://www.statisticshowto.com/probability-and-statistics/coefficient-of-determination-r-squared/
# Pearson's correlation coefficient
numerator = np.sum((x - x_mean)*(y - y_mean))
denominator = ( np.sum((x - x_mean)**2) * np.sum((y - y_mean)**2) )**.5
correlation_coef = numerator / denominator
r2 = correlation_coef**2

# mean squared error
MSE = 1/n * np.sum( (y - y_model)**2 )

# to plot the adjusted model
x_line = np.linspace(np.min(x), np.max(x), 100)
y_line = np.polyval([slope, intercept], x_line)

# confidence interval
ci = t * std_error * (1/n + (x_line - x_mean)**2 / np.sum((x - x_mean)**2))**.5
# predicting interval
pi = t * std_error * (1 + 1/n + (x_line - x_mean)**2 / np.sum((x - x_mean)**2))**.5  

############### Ploting
plt.rcParams.update({'font.size': 14})
fig = plt.figure()
ax = fig.add_axes([.1, .1, .8, .8])

ax.plot(x, y, 'o', color = 'royalblue')
ax.plot(x_line, y_line, color = 'royalblue')
ax.fill_between(x_line, y_line + pi, y_line - pi, color = 'lightcyan', label = '95% prediction interval')
ax.fill_between(x_line, y_line + ci, y_line - ci, color = 'skyblue', label = '95% confidence interval')

ax.set_xlabel('x')
ax.set_ylabel('y')

# rounding and position must be changed for each case and preference
a = str(np.round(intercept))
b = str(np.round(slope,2))
r2s = str(np.round(r2,2))
MSEs = str(np.round(MSE))

ax.text(45, 110, 'y = ' + a + ' + ' + b + ' x')
ax.text(45, 100, '$r^2$ = ' + r2s + '     MSE = ' + MSEs)

plt.legend(bbox_to_anchor=(1, .25), fontsize=12)

Rissa

Answer 4

For a project of mine, I needed to create intervals for time-series modeling, and to make the procedure more efficient I created tsmoothie: A python library for time-series smoothing and outlier detection in a vectorized way.

It provides different smoothing algorithms together with the possibility to computes intervals.

In the case of linear regression:

import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.smoother import *
from tsmoothie.utils_func import sim_randomwalk

# generate 10 randomwalks of length 50
np.random.seed(33)
data = sim_randomwalk(n_series=10, timesteps=50, 
                      process_noise=10, measure_noise=30)

# operate smoothing
smoother = PolynomialSmoother(degree=1)
smoother.smooth(data)

# generate intervals
low_pi, up_pi = smoother.get_intervals('prediction_interval', confidence=0.05)
low_ci, up_ci = smoother.get_intervals('confidence_interval', confidence=0.05)

# plot the first smoothed timeseries with intervals
plt.figure(figsize=(11,6))
plt.plot(smoother.smooth_data[0], linewidth=3, color='blue')
plt.plot(smoother.data[0], '.k')
plt.fill_between(range(len(smoother.data[0])), low_pi[0], up_pi[0], alpha=0.3, color='blue')
plt.fill_between(range(len(smoother.data[0])), low_ci[0], up_ci[0], alpha=0.3, color='blue')

In the case of regression with order bigger than 1:

# operate smoothing
smoother = PolynomialSmoother(degree=5)
smoother.smooth(data)

# generate intervals
low_pi, up_pi = smoother.get_intervals('prediction_interval', confidence=0.05)
low_ci, up_ci = smoother.get_intervals('confidence_interval', confidence=0.05)

# plot the first smoothed timeseries with intervals
plt.figure(figsize=(11,6))
plt.plot(smoother.smooth_data[0], linewidth=3, color='blue')
plt.plot(smoother.data[0], '.k')
plt.fill_between(range(len(smoother.data[0])), low_pi[0], up_pi[0], alpha=0.3, color='blue')
plt.fill_between(range(len(smoother.data[0])), low_ci[0], up_ci[0], alpha=0.3, color='blue')

I point out also that tsmoothie can carry out the smoothing of multiple time-series in a vectorized way. Hope this can help someone

Rumph