Clock cycles required for multiplication and addition operations [duplicate]

Question

A question I have on Problem 5.5 of the book Computer Systems: A Programmer's Perspective about clock cycles required to perform arithmetic operations:

For context, clock cycles required for each operation has been given as:

So for ‘double’ operations, ‘addition’ costs 3 cycles, ‘multiplication’ 5 cycles.
I would think that for each loop, line 7 would dictate the cost as it needs an addition and a multiplication, meaning cost would be ‘3 + 5’.
However the standard answer is that line 8 is actually the limit, and therefore the cost for each loop is 5 cycles:

Could anyone help me understand why is the limit line 8 but not line 7?

---

Attaching the similar follow up question 5.6 and its answer too, where the limit is calculated as ‘5 + 3’ this time

Arana

how is Intel related here? Does the book specifically talk about x86? – Improvisatory

Yes all experiments are carried out on Intel i7 Haswell – Arana

Does the compiler convert the a[i] (in result += a[i] * xpwr;) into something like *(double *) ( ( void *)a + sizeof(double) * i); with an addition and a multiplication; or does the compiler lift it out of the loop like result += *(double *)tempAddress * xpwr; and tempAddress += sizeof(double); so there's an addition but no multiplication, or does the compiler use a CPU's complex addressing modes (e.g. like "mov rax,[rsi+rcx*8]` on 80x86) and pretend that the addition is not an addition (and pretend the shift isn't a shift or multiplication)? – Newfoundland

If you don't know how many additions or multiplications the a[i] is, then... ;-) – Newfoundland

@Brendan: nitpicking "adds and muls" vs. "floating point adds and muls" has already been done in How to count the number of computations in the loop?. Interesting point about the address math; there's also the i++ loop-carried dep chain, but that's only integer so it can easily get unrolled. Pretty clearly the book authors meant to ask for counts of FP math operations, the expensive ones in this case. Unfortunately they didn't explicitly say that. :/ – Wandie

Answer 1

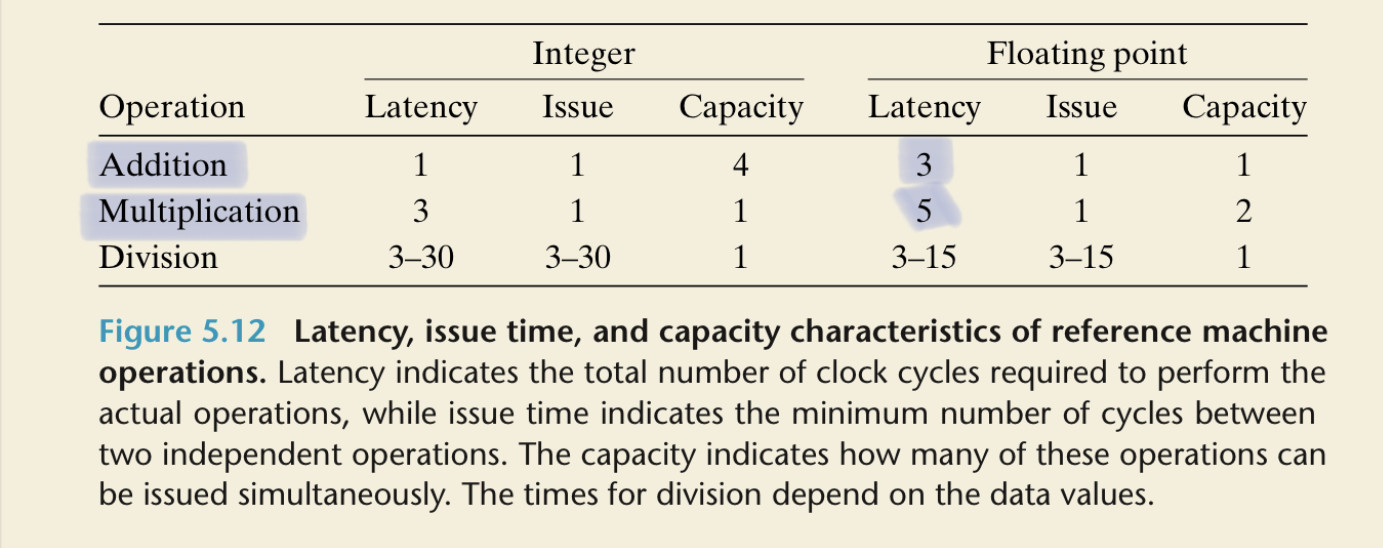
In problem 5.5, each calculation of xpwr depends on the previous calculation of xpwr (in the absence of aggressive optimization by the compiler, such as loop unrolling), so it must wait the full latency of a multiplication.

The calculation of result depends on a previous addition to result and a multiplication that can be done in parallel. The addition has a lower latency than the multiplication, so it does not limit the computation.

In more detail, what will typically happen for the floating-point operations in the CPU (ignoring loads, integer operations, and so on) is something like:

• Cycle 0: a[i] * xpwr will be started (for i = 0).
• Cycle 0: result += a[i] * xpwr cannot be started because it has to wait for a[i] * xpwr.
• Cycle 0: x * xpwr is started. (I assume we can start both of these in cycle 0 because the text says the capacity for issuing multiplications is 2 per cycle. It also says there has to be 1 cycle between issuing independent operations, but I do not see the sense of that given the capacity is 2 per cycle.)
• Cycle 5: a[i] * xpwr and x * xpwr finish.
• Cycle 5: result += a[i] * xpwr is started (for i = 0).
• Cycle 5: a[i] * xpwr is started (for i = 1).
• Cycle 5: x * xpwr is started.
• Cycle 8: result += a[i] * xpwr finishes.
• Cycle 8: result += a[i] * xpwr (for i = 1) cannot start because its xpwr is not available.
• Cycle 10: a[i] * xpwr and x * xpwr finish.
• Cycle 10: result += a[i] * xpwr is started (for i = 1).
• Cycle 10: a[i] * xpwr is started (for i = 2).
• Cycle 10: x * xpwr is started.
• Cycle 13: result += a[i] * xpwr finishes.

Then everything repeats on a five-cycle period.

In problem 5.6, result = a[i] + x*result means that, after we get the previous value of result, it takes five cycles to compute x*result, and we cannot start the addition until we have the result of that multiplication. Then it takes three cycles to compute a[i] + x*result, so it takes eight cycles from getting one result to getting the next one.

Grow

Thanks @Eric, in this case I could say line 7 & 8 are equally expansive? And I guess this doesn’t quite explain why question 5.6’s anyswer says it costs 8 cycles as we should be able to parallelise it too? – Arana

@waynewingsyd: In terms of throughput cost on Skylake, yes. On Haswell, sort of; only one port can run addsd / addpd instructions, competing with mulpd. But the latency bottleneck prevents you from coming close to the throughput bottlenecks. Anyway, in 5.5 there are two parallel loop-carried dep chains that run in lockstep, with the faster one having to wait for inputs from the slower one (multiply). See my answer on Latency bounds and throughput bounds for processors for operations that must occur in sequence for a graph of the data dependencies. – Wandie

@waynewingsyd: 5.6 is different, look at the dependency chain from one result to the next. If you don't contract the operations into one FMA (with 5-cycle latency), it's a mul and then an add before either of those ops next iteration can start. (FMA makes Horner's method quite good, especially for throughput when the polynomial is only 5th or 6th order so out-of-order exec can overlap that dep chain with surrounding work). That other Q&A I linked asked about that, too. – Wandie