Mandelbrot Set - Color Spectrum Suggestions?

Question

Recently I started making Mandelbrot set, but I wasn't able to find a good color spectrum. Here's my result

But I want to create something like this:

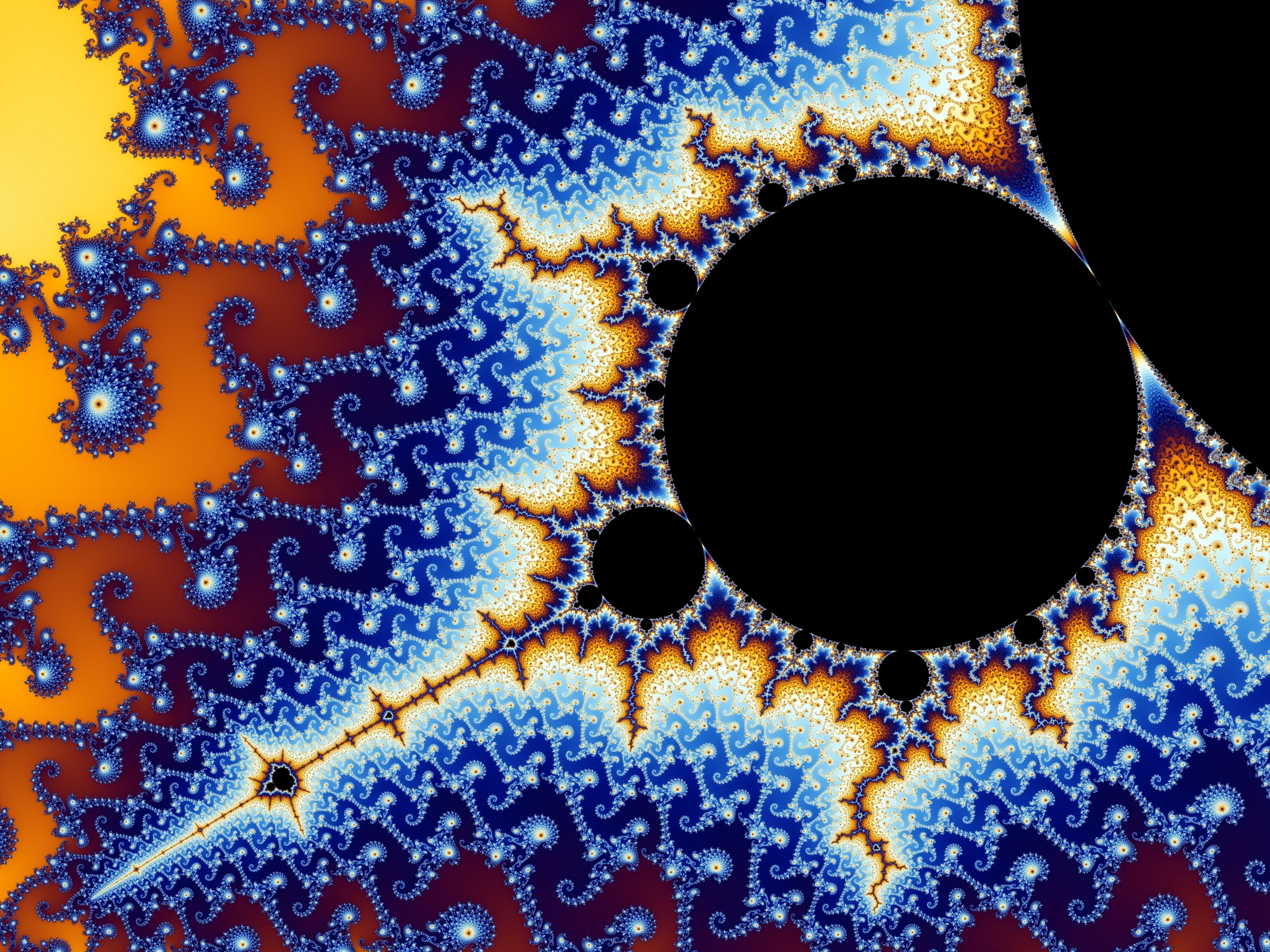
Any Suggestions? Thanks!

Biddle

Answer 1

1. try using computed palette instead of texture

   For example this is mine:

   • RGB values of visible spectrum

2. higher details need higher iteration counts

   so how many iterations you got? If I apply #1 and use n=200 iterations this:

   • GLSL Mandelbrot Set

   I got this:

   Which more or less resembles your case (apart the aspect ratio, but still not sure we have the same set...). The number of iterations not only affect the details count but also the owerall brightness of the result so be careful not to use too much or too less.

3. zoom

   Once you start zooming the details will start appearing in much more depth ... This is n=2000 and zoomed the third copy from the right ...

   as yo can see there is a lot of details that aren't visible in the previous image

4. further improvement

   you can use non linear scales to map from iteration to color. So again the same zoom but with using t=pow(t,0.5); as parameter for color...

   As you can see the result looks better (more smooth)...

   Last thing that I can think of is to implement sort of HDR ... so compute first base image with small n then inspect it and find zones with low detail (almost no color change) and re-render them with higher n until you got no such zones... For each n you can tweak the parameter delinearization function a bit ...

   Also you can find the min and max parameter for the whole result and compute the color from only that range covering whole spectrum from that ... like:

   l = 400 + 300*(i-imin)/(imax-imin)
   

   where l is wavelength in [nm] for the color spectrum , i is the final iteration and imin,imax are the min and max values for whole image ... sadly I can not try it easily as I would need to rewrite the GLSL render to two pass renderer.

   Another thing you can do is use histogram instead of min max ... but this is also multi pass technique ...

[Edit1] match

Also while comparing to foreign images make sure they use the same set ... otherwise you are comparing oranges with apples. When I took closer look its obvious I got the same set just different scale on x ... and the view is zoomed on specific point of the fractal. After some tweaking the closest match I found was this:

[Edit2] histogram

After modifying my code to support multipass rendering I could apply histogram approach... So

1. render Mandelbrot Set to Texture

   but instead of colors render the iteration index ...

2. compute histogram of the rendered stuff

3. find range of indexes to recolor

   the histogram will have many entries with zero or small pixel count... and then there will be group of higher values (that is the range you are seeking) and after that there will be small or zero values again... On top of all this the last value can contain a large amount of pixels (thats the black empty area) and there might be one or some more very high values too independent of the major group. If I use 80% of the spectral colors for the main group/range and 10% for indexes before it and 10% for indexes after it the result looks like this:

Here the modified GLSL code with repaired scale, zoom and switch between singe/multi pass rendering:

// Vertex
#version 420 core
layout(location=0) in vec2 pos;     // glVertex2f <-1,+1>
out smooth vec2 p;                  // texture end point <0,1>
void main()
    {
    p=pos;
    gl_Position=vec4(pos,0.0,1.0);
    }

// Fragment
#version 420 core
#define multi_pass
uniform vec2 p0=vec2(0.0,0.0);      // mouse position <-1,+1>
uniform float zoom=1.000;           // zoom [-]
uniform int  n=4000;                // iterations [-]
in smooth vec2 p;
out vec4 col;
#ifdef multi_pass
vec3 spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  vec3 c=vec3(0.0,0.0,0.0);
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); c.r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); c.r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); c.r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); c.r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); c.r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); c.g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); c.g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); c.g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); c.b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); c.b=0.7 -(     t)+(0.30*t*t); }
    return c;
    }
#endif
void main()
    {
    int i,j;
    vec2 pp;
    float x,y,q,xx,yy;
    pp=(p/zoom)-p0;         // y (-1.0, 1.0)
    pp.x-=0.5;              // x (-1.5, 0.5)
    for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n)&&(xx+yy<4.0);i++)
        {
        q=xx-yy+pp.x;
        y=(2.0*x*y)+pp.y;
        x=q;
        xx=x*x;
        yy=y*y;
        }
    #ifndef multi_pass
    // RGB
    q=float(i)/float(n);
    q=pow(q,0.2);
    col=vec4(spectral_color(400.0+(300.0*q)),1.0);
    #else
    // i
    float r,g,b;
    r= i     &255; r/=255.0;
    g=(i>> 8)&255; g/=255.0;
    b=(i>>16)&255; b/=255.0;
    col=vec4(r,g,b,255);
    #endif
    }

Image is taken for

n=4095;            // max iterations
zoom=1763.0;       // zoom [-]
p0.x=0.1483064;    // center position
p0.y=0.3742866;

And the second pass render is like this:

// globals
const int N=4095; // this is the max count of iterations
OpenGLtexture txr;

// helper functions
DWORD spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  float r,g,b; DWORD c,x; r=0.0; g=0.0; b=0.0;
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); b=0.7 -(     t)+(0.30*t*t); }
    r*=255.0; g*=255.0; b*=255.0;
    x=r; c =x;
    x=g; c|=x<<8;
    x=b; c|=x<<16;
    return c;
    }

    ...
    // [multipass] this is executed after the shader renders its stuff
    int hist[N+1],sz=txr.xs*txr.ys,i,i0,i1,a0,a1;
    float t;
    // get rendered image
    glReadPixels(0,0,txr.xs,txr.ys,GL_RGBA,GL_UNSIGNED_BYTE,txr.txr);
    // compute histogram
    for (i=0;i<N;i++) hist[i]=0;
    for (i=0;i<sz;i++) hist[txr.txr[i]&0x00FFFFFF]++;
    // find the major used range
    a0=txr.xs/4;
    a1=txr.xs*4;
    for (i0=  0;(i0<N)&&((hist[i0]<a0)||(hist[i0]>a1));i0++);
    for (i1=N-1;(i1>0)&&((hist[i1]<a0)||(hist[i1]>a1));i1--);
    // recolor it
    for (i=0;i<sz;i++)
        {
        a0=txr.txr[i]&0x00FFFFFF;
             if (a0<i0) t=(0.1*divide(a0   ,i0   ));
        else if (a0>i1) t=(0.1*divide(a0-i1,N -i1))+0.9;
        else            t=(0.8*divide(a0-i0,i1-i0))+0.1;
        txr.txr[i]=spectral_color(400.0+(300.0*t));
        }
    // render it back
    scr.cls();
    txr.bind();
    glColor3f(1.0,1.0,1.0);
    glBegin(GL_QUADS);
    glTexCoord2f(0.0,1.0); glVertex2f(-1.0,+1.0);
    glTexCoord2f(0.0,0.0); glVertex2f(-1.0,-1.0);
    glTexCoord2f(1.0,0.0); glVertex2f(+1.0,-1.0);
    glTexCoord2f(1.0,1.0); glVertex2f(+1.0,+1.0);
    glEnd();
    txr.unbind();
    glDisable(GL_TEXTURE_2D);

I know its use a lot of stuff I did not share but the histogram usage is straightforward enough to port it to your needs...

So now its just a matter of finding the correct combination of n and position/zoom.

[Edit3] However if even this is not enough

Then you can implement fractional escape for more info see:

• Can't find a way to color the Mandelbrot-set the way i'm aiming for

Stralsund

Answer 2

In the deeper zoom, not only are the contours much closer together than in the base image (the "landscape" rises more steeply), but the palette used has smaller transitions. The palette used in the base image has a large step in colour values between adjacent contours, taking only 9 steps to go from deep blue to yellow.

If you use a single value step in just one of the three primaries from one contour to the next, you can still discern the difference but it is less obvious, appearing far more smooth. I would do this with a precalculated look-up table.

Bistro