Can't find a way to color the Mandelbrot-set the way i'm aiming for

I've been successful in coloring the Mandelbrot-set although I can't zoom in very far until it becomes "blurry" and the pattern stops. I fix this by increasing the max_iteration, this works but I get very few colors at *1 magnification and lot's of colors only appear when I zoom in. I understand why this happens since in a "true" Mandelbrot-set there are no colors and increasing the max_iterations just brings it closer to that. But my question is, is how do zooms such as on youtube have beautiful colors throughout the whole zooming process while still being able to zoom on for what feels like forever?

I've tried looking everywhere online but I can't find a solution and when I look in the descriptions of these youtube zooms they seem to provide barely anything on how they made that zoom.

Here is just the section of code which draws the Mandelbrot set. The code below is written in processing which is java with added visual libraries. You can find out more about the program here: https://processing.org/

//m is max_iterations
//mb is the function which calculates how many iterations each point took to escape to infinity. I won't be including the function since I know it works fine and it's quite messy.
//i'm using a HSB/HSV system to draw the mandelbrot

hue=(mb(x, y, m)*360)/m;
sat=255;
if (mb(x, y, m)<m) {
  val=255;
} 
else {
  val=0;
}

stroke(hue,sat,val);
point(x, y);

I understand why my problem is happening but I don't know how to solve it.

Here is an image with a low max_iterations and zoomed out, as you can see it's very colorful:

Here is an image with a low max_iterations and zoomed in slightly, as you can see it's boring and not very colorful:

Here is an image with a high max_iterations and zoomed out, as you can see it's not very colorful:

Here is an image with a high max_iterations and zoomed in, as you can see it's very colorful:

First take a look at this related QA:

Mandelbrot Set - Color Spectrum Suggestions?

The main idea is to use histogram to distribute the color gradients more effectively to used indexes instead of uniformly wasting many colors on unused indexes. Also it uses a specific visually pleasing gradient function:

RGB values of visible spectrum

Dynamic max iterations count suggested by others will only affect overall performance and details in zooms. However if you want nice colors without zoom then you need to compute floating point iterations count which is also called Mandelbrot Escape. There is a math way that can compute the iterations count fractional part from the last sub-results of the equation. For more info see:

Renormalizing the Mandelbrot Escape

However I never tried it so read this with prejudice: If I read it right what you want is to compute this equation:

mu = m + frac = n + 1 - log (log  |Z(n)|) / log 2

Where n is your iteration count, Z(n) is the complex domain sub-result of the equation you are iterating on. So now compute color from mu which is floating point now instead of from n...

[Edit2] GLSL mandelbrot with fractional escape based on links above

I added the fractional escape and modified the histogram multi pass recoloring to match new output...

Vertex:

// Vertex
#version 420 core
layout(location=0) in vec2 pos;     // glVertex2f <-1,+1>
out smooth vec2 p;                  // texture end point <0,1>
void main()
    {
    p=pos;
    gl_Position=vec4(pos,0.0,1.0);
    }

Fragment:

// Fragment
#version 420 core
uniform vec2 p0=vec2(0.0,0.0);      // mouse position <-1,+1>
uniform float zoom=1.000;           // zoom [-]
uniform int  n=100;                 // iterations [-]
uniform int  sh=7;                  // fixed point accuracy [bits]
uniform int  multipass=0;           // multi pass?
in smooth vec2 p;
out vec4 col;

const int n0=1;                     // forced iterations after escape to improve precision

vec3 spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  vec3 c=vec3(0.0,0.0,0.0);
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); c.r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); c.r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); c.r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); c.r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); c.r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); c.g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); c.g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); c.g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); c.b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); c.b=0.7 -(     t)+(0.30*t*t); }
    return c;
    }

void main()
    {
    int i,j,N;
    vec2 pp;
    float x,y,q,xx,yy,mu;
    pp=(p/zoom)-p0;         // y (-1.0, 1.0)
    pp.x-=0.5;              // x (-1.5, 0.5)
    for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n-n0)&&(xx+yy<4.0);i++)
        {
        q=xx-yy+pp.x;
        y=(2.0*x*y)+pp.y;
        x=q;
        xx=x*x;
        yy=y*y;     
        }
    for (j=0;j<n0;j++,i++)  // 2 more iterations to diminish fraction escape error
        {
        q=xx-yy+pp.x;
        y=(2.0*x*y)+pp.y;
        x=q;
        xx=x*x;
        yy=y*y;
        }
    mu=float(i)-log(log(sqrt(xx+yy))/log(2.0));
    mu*=float(1<<sh); i=int(mu);
    N=n<<sh;
    if (i>N) i=N;
    if (i<0) i=0;

    if (multipass!=0)
        {
        // i
        float r,g,b;
        r= i     &255; r/=255.0;
        g=(i>> 8)&255; g/=255.0;
        b=(i>>16)&255; b/=255.0;
        col=vec4(r,g,b,255);
        }
    else{
        // RGB
        q=float(i)/float(N);
        q=pow(q,0.2);
        col=vec4(spectral_color(400.0+(300.0*q)),1.0);
        }
    }

CPU side C++/VCL code:

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include "Unit1.h"
#include "gl\\OpenGL3D_double.cpp"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
OpenGLscreen scr;
GLSLprogram shd;
float mx=0.0,my=0.0,mx0=0.0,my0=0.0,mx1=0.0,my1=0.0;
TShiftState sh0,sh1;
int xs=1,ys=1;
float zoom=1.000;
int sh=7;
int N=256;
int _multi=0;
unsigned int queryID[2];
#define multi_pass
OpenGLtexture txr;
//---------------------------------------------------------------------------
DWORD spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  float r,g,b; DWORD c,x; r=0.0; g=0.0; b=0.0;
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); b=0.7 -(     t)+(0.30*t*t); }
    r*=255.0; g*=255.0; b*=255.0;
    x=r; c =x;
    x=g; c|=x<<8;
    x=b; c|=x<<16;
    return c;
    }
//---------------------------------------------------------------------------
void gl_draw()
    {
    scr.cls();

    // matrix for old GL rendering
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    glMatrixMode(GL_TEXTURE);
    glLoadIdentity();


    // GLSL uniforms
    shd.bind();
    shd.set2f("p0",mx,my);          // pan position
    shd.set1f("zoom",zoom);         // zoom
    shd.set1i("n",N);               // iterations
    shd.set1i("sh",sh);             // fixed point accuracy (shift)
    shd.set1i("multipass",_multi);  // single/multi pass

    // issue the first query
    // Records the time only after all previous
    // commands have been completed
    glQueryCounter(queryID[0], GL_TIMESTAMP);

    // QUAD covering screen
    glColor3f(1.0,1.0,1.0);
    glBegin(GL_QUADS);
    glVertex2f(-1.0,+1.0);
    glVertex2f(-1.0,-1.0);
    glVertex2f(+1.0,-1.0);
    glVertex2f(+1.0,+1.0);
    glEnd();
    shd.unbind();

    // [multipas]
    if (_multi)
        {
        float t,m,n=N<<sh;
        DWORD *hist=new DWORD[n+1];
        int sz=txr.xs*txr.ys,i,j;
        // get rendered image
        glReadPixels(0,0,txr.xs,txr.ys,GL_RGBA,GL_UNSIGNED_BYTE,txr.txr);
        // compute histogram
        for (i=0;i<=n;i++) hist[i]=0;
        for (i=0;i<sz;i++) hist[txr.txr[i]&0x00FFFFFF]++;
        // histogram -> used color index (skip holes)
        for (i=1,j=1;i<=n;i++)
         if (hist[i]){ hist[i]=j; j++; }
        // used color index -> color
        m=1.0/float(j); hist[0]=0x00000000;
        for (i=1;i<=n;i++)
         if (hist[i]){ t=hist[i]; t*=m; hist[i]=spectral_color(400.0+(300.0*t)); }
          else hist[i]=0x00000000;
        // recolor image
        for (i=0;i<sz;i++) txr.txr[i]=hist[txr.txr[i]&0x00FFFFFF];
        // render it back
        scr.cls();
        txr.bind();
        glColor3f(1.0,1.0,1.0);
        glBegin(GL_QUADS);
        glTexCoord2f(0.0,1.0); glVertex2f(-1.0,+1.0);
        glTexCoord2f(0.0,0.0); glVertex2f(-1.0,-1.0);
        glTexCoord2f(1.0,0.0); glVertex2f(+1.0,-1.0);
        glTexCoord2f(1.0,1.0); glVertex2f(+1.0,+1.0);
        glEnd();
        txr.unbind();
        glDisable(GL_TEXTURE_2D);
        delete[] hist;
        }

    // issue the second query
    // records the time when the sequence of OpenGL
    // commands has been fully executed
    glQueryCounter(queryID[1], GL_TIMESTAMP);


    // GL driver info and GLSL log
    scr.text_init_pix(0.75);
    glColor4f(1.0,1.0,1.0,0.9);
    scr.text(glGetAnsiString(GL_VENDOR));
    scr.text(glGetAnsiString(GL_RENDERER));
    scr.text("OpenGL ver: "+glGetAnsiString(GL_VERSION));
    if (_multi) scr.text("Multi pass");
     else       scr.text("Single pass");
    if (shd.log.Length()!=41)
     for (int i=1;i<=shd.log.Length();) scr.text(str_load_lin(shd.log,i,true));
    scr.text_exit();

    scr.exe();
    scr.rfs();

    // wait until the results are available
    int e;
    unsigned __int64 t0,t1;
    for (e=0;!e;) glGetQueryObjectiv(queryID[0],GL_QUERY_RESULT_AVAILABLE,&e);
    for (e=0;!e;) glGetQueryObjectiv(queryID[1],GL_QUERY_RESULT_AVAILABLE,&e);
    glGetQueryObjectui64v(queryID[0], GL_QUERY_RESULT, &t0);
    glGetQueryObjectui64v(queryID[1], GL_QUERY_RESULT, &t1);
    Form1->Caption=AnsiString().sprintf("dt: %f ms p0:%.3fx%.3f zoom: %.1lf N:%i<<%i\n",(t1-t0)/1000000.0,mx,my,zoom,N,sh);
    }
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner):TForm(Owner)
    {
    scr.init(this);
    shd.set_source_file("","","","Mandelbrot_set.glsl_vert","Mandelbrot_set.glsl_frag");
    glGenQueries(2, queryID);
    // nice spirals
    _multi=1;
    zoom=300.0;
    mx  = 0.268;
    my  =-0.102;
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormDestroy(TObject *Sender)
    {
    scr.exit();
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormResize(TObject *Sender)
    {
    scr.resize();
    xs=ClientWidth;
    ys=ClientHeight;
    txr.resize(xs,ys);
    gl_draw();
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormPaint(TObject *Sender)
    {
    gl_draw();
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormMouseMove(TObject *Sender, TShiftState Shift, int X,int Y)
    {
    bool q0,q1;
    mx1=1.0-divide(X+X,xs-1);
    my1=divide(Y+Y,ys-1)-1.0;
    sh1=Shift;
    q0=sh0.Contains(ssLeft);
    q1=sh1.Contains(ssLeft);
    if (q1)
        {
        mx-=(mx1-mx0)/zoom;
        my-=(my1-my0)/zoom;
        }
    mx0=mx1; my0=my1; sh0=sh1;
    gl_draw();
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormMouseDown(TObject *Sender, TMouseButton Button,TShiftState Shift, int X, int Y)
    {
    FormMouseMove(Sender,Shift,X,Y);
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormMouseUp(TObject *Sender, TMouseButton Button,TShiftState Shift, int X, int Y)
    {
    FormMouseMove(Sender,Shift,X,Y);
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormMouseWheel(TObject *Sender, TShiftState Shift, int WheelDelta, TPoint &MousePos, bool &Handled)
    {
    if (WheelDelta>0) zoom*=1.2;
    if (WheelDelta<0) zoom/=1.2;
    Handled=true;
    gl_draw();
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormKeyDown(TObject *Sender, WORD &Key, TShiftState Shift)
    {
    Caption=Key;
    if (Key==32){ _multi=!_multi; gl_draw(); }      // [Space]
    if (Key==33){ if (N<8192) N<<=1; gl_draw(); }   // [PgUp]
    if (Key==34){ if (N> 128) N>>=1; gl_draw(); }   // [PgDown]
    }
//---------------------------------------------------------------------------

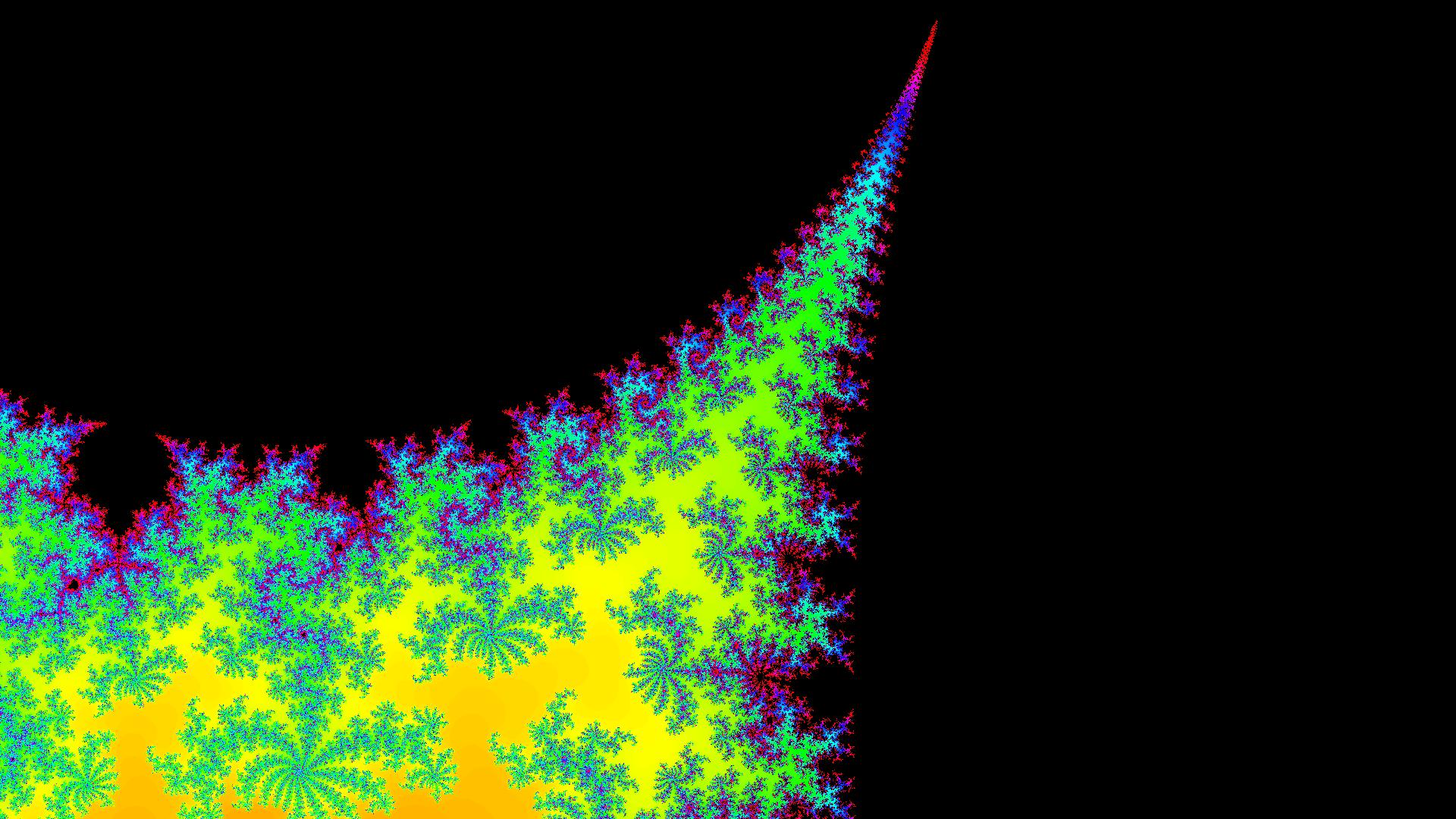
This is single pass fractional escape n=100*32:

$fractional escape$

This is single pass integer escape n=100:

As you can see the fractional escape is much better for the same number of iterations (100).

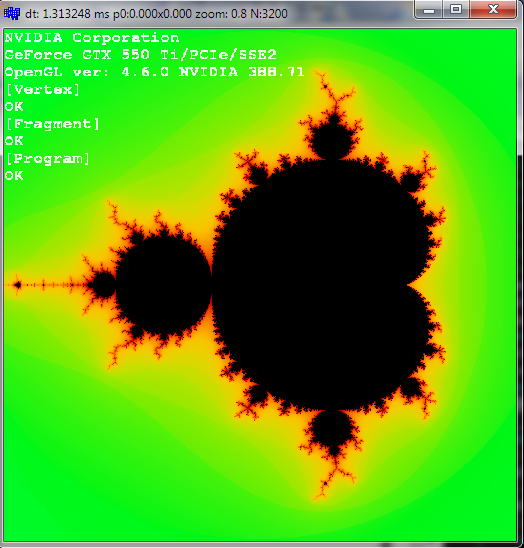
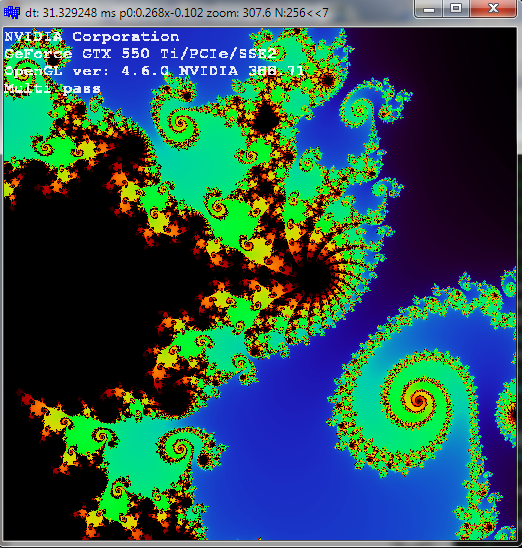
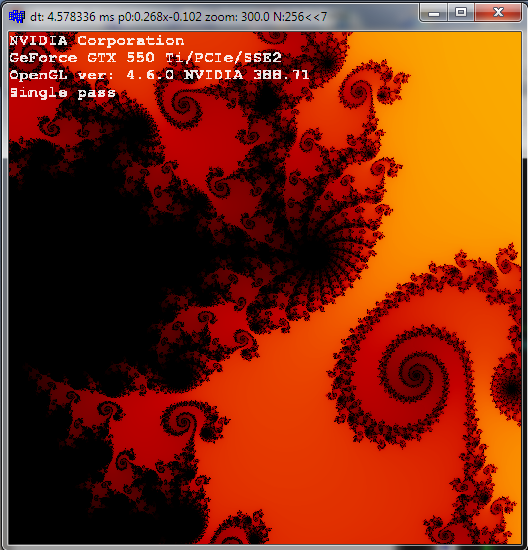
And finally nice multi pass (as a showoff) only 256 iterations and ~300x zoom:

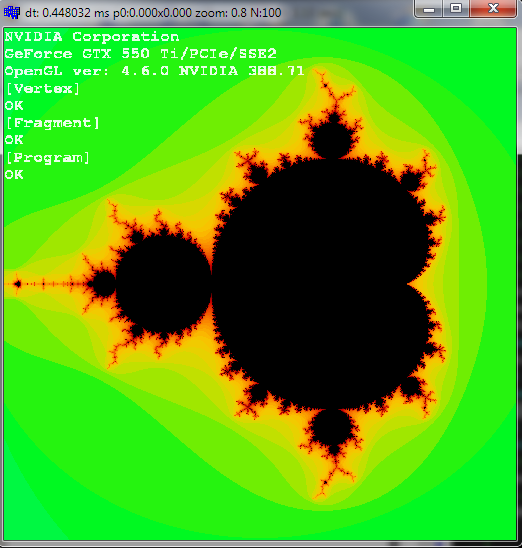
versus single pass:

Some explanations on the modification:

I added sh fractional bits part to the counter (fixed point). So the max count is now n<<sh instead of just n. I also added n0 constant that lowers the error of fractional part of escape. The link suggest to use 2 iterations but 1 looks better I think (It also removes the i+1 increment from the logarithmic equation). The iteration loop is unchanged I just add the same n0 iterations after it and then compute the fractional escape mu and convert it to fixed point (as my shader outputs integer).

Multi pass is changed only on the CPU side code. It simply re-index the used indexes so there are no holes in them and recolor using visible spectra colors.

Here Demo:

Recommended topics

Hot tags