It is highly important to select the hyperparameters of DBSCAN algorithm rightly for your dataset and the domain in which it belongs.
eps hyperparameter
In order to determine the best value of eps for your dataset, use the K-Nearest Neighbours approach as explained in these two papers: Sander et al. 1998 and Schubert et al. 2017 (both papers from the original DBSCAN authors).
Here's a condensed version of their approach:
If you have N-dimensional data to begin, then choose n_neighbors in sklearn.neighbors.NearestNeighbors to be equal to 2xN - 1, and find out distances of the K-nearest neighbors (K being 2xN - 1) for each point in your dataset. Sort these distances out and plot them to find the "elbow" which separates noisy points (with high K-nearest neighbor distance) from points (with relatively low K-nearest neighbor distance) which will most likely fall into a cluster. The distance at which this "elbow" occurs is your point of optimal eps.
Here's some python code to illustrate how to do this:
def get_kdist_plot(X=None, k=None, radius_nbrs=1.0):
nbrs = NearestNeighbors(n_neighbors=k, radius=radius_nbrs).fit(X)
# For each point, compute distances to its k-nearest neighbors
distances, indices = nbrs.kneighbors(X)
distances = np.sort(distances, axis=0)
distances = distances[:, k-1]
# Plot the sorted K-nearest neighbor distance for each point in the dataset
plt.figure(figsize=(8,8))
plt.plot(distances)
plt.xlabel('Points/Objects in the dataset', fontsize=12)
plt.ylabel('Sorted {}-nearest neighbor distance'.format(k), fontsize=12)
plt.grid(True, linestyle="--", color='black', alpha=0.4)
plt.show()
plt.close()
k = 2 * X.shape[-1] - 1 # k=2*{dim(dataset)} - 1
get_kdist_plot(X=X, k=k)
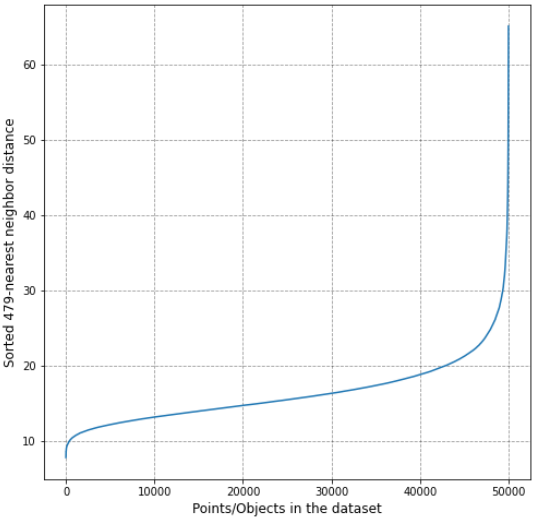
Here's an example resultant plot from the code above:
![]()
From the plot above, it can be inferred that the optimal value for eps can be assumed at around 22 for the given dataset.
NOTE: I would strongly advice the reader to refer to the two papers cited above (especially Schubert et al. 2017) for additional tips on how to avoid several common pitfalls when using DBSCAN as well as other clustering algorithms.
There are a few articles online –– DBSCAN Python Example: The Optimal Value For Epsilon (EPS) and CoronaVirus Pandemic and Google Mobility Trend EDA –– which basically use the same approach but fail to mention the crucial choice of the value of K or n_neighbors as 2xN-1 when performing the above procedure.
min_samples hyperparameter
As for the min_samples hyperparameter, I agree with the suggestions in the accepted answer. Also, a general guideline for choosing this hyperparameter's optimal value is that it should be set to twice the number of features (Sander et al. 1998). For instance, if each point in the dataset has 10 features, a starting point to consider for min_samples would be 20.