OpenGL Ellipse with start/end angle issues

Question

I'm having an issue with drawing an ellipse object using OpenGL (sharpgl to be exact since it works well enough with WPF).

Right now I'm using this code (angles are in degrees):

gl.Begin(OpenGL.GL_LINE_STRIP);
gl.Color(colorR, colorG, colorB, alfa);
for (double i = angleStart; i <= angleEnd; ++i)
{
    double angleCurrent = Math.PI * i / 180;

    double dx = radiusX * Math.Cos(angleCurrent);
    double dy = radiusY * Math.Sin(angleCurrent);

    gl.Vertex(dx + ellipseMiddleCoordX, dy + ellipseMiddleCoordY, 0);
}

gl.End();

And it works 100% fine for drawing circles (that is radiusX = radiusY) and ellipses where angles are 0, 90, 180, 270, 360 (radiusX != radiusY).

However it doesn't quite do the job when radiusX != radiusY and for example angleStart = 30; angleEnd = 70.

What it does for above example it draws a circle first, apply the angles, then recalculates the X/Y radius. This gives incorrect results since I expect something like this:

where red = expected behaviour, yellow = code above, grey = additional lines for angles

I'm quite lost on how I'm suppose to approach the fix in this.

P.S. yes - I know that gl.Begin/gl.End are outdated functions, but I still fail to grasp the full concept of OGL, and most of my program is just math.

Kappel

Answer 1

That is because the elliptic parametric angle is not geometric angle as it is distorted by the different scale (radius) in each axis. See these related QAs for some inspiration:

• I need an equation for equal movement along an ellipse
• Algorithm for shape calculation (Ellipse)

The way to solve this is ether approximate the distortion (but that will beproblematic if eccentricity change a lot) or search for correct angle (simple but slow) or compute it analytically (involves some math but fast).

For the search you can use binary search for this just take in mind the geometric angle will be bigger than parametric one on some quadrants and less on the others.

Here small C++/OpenGL example (unsophisticated and unoptimized to keep it as simple as possible):

//---------------------------------------------------------------------------
const float pi2=2.0*M_PI;
const float deg=M_PI/180.0;
//---------------------------------------------------------------------------
float ellipse_angle(float rx,float ry,float ang)    // geometrical angle [rad] -> ellipse parametric angle [rad]
    {
    float da,ea,ga;
    ang=fmod(ang,pi2);                              // normalize to <0,pi2>
    ea=ang;                                         // start elliptic angle
    ga=atan2(ry*sin(ea),rx*cos(ea));                // compute geometrical angle from it
    if (ga<0.0) ga+=pi2;                            // normalize to <0,pi2>
    if (ga<=ang)                                    // ea >= ang
        {
        da=90.0*deg-fmod(ang,90.0*deg);             // range to search
        da*=0.5;
        for (ea=ang;da>1e-10;da*=0.5)               // binary search
            {
            ea+=da;                                 // test next elliptic angle
            ga=atan2(ry*sin(ea),rx*cos(ea));        // compute geometrical angle from it
            if (ga<0.0) ga+=pi2;                    // normalize to <0,pi2>
            if (ga>ang) ea-=da;                     // restore original angle if too big
            }
        }
    else{                                           // ea <= ang
        da=fmod(ang,90.0*deg);                      // range to search
        da*=0.5;
        for (ea=ang;da>1e-10;da*=0.5)               // binary search
            {
            ea-=da;                                 // test next elliptic angle
            ga=atan2(ry*sin(ea),rx*cos(ea));        // compute geometrical angle from it
            if (ga<0.0) ga+=pi2;                    // normalize to <0,pi2>
            if (ga<ang) ea+=da;                     // restore original angle if too small
            }
        }

    return ea;
    }
//---------------------------------------------------------------------------
void gl_draw()
    {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    glScalef(1.0,float(xs)/float(ys),1.0);
    glMatrixMode(GL_TEXTURE);
    glLoadIdentity();
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    glDisable(GL_DEPTH_TEST);

    int i,n=100;
    float rx=0.75,ry=0.5,a0=25.0*deg,a1=115.0*deg;
    float x,y,a,da,ea0,ea1,dd;

    // test whole circumference
    for (dd=10.0*deg,a0=0.0,a1=a0+0.75*dd;a1<pi2;a0+=dd,a1+=dd)
        {
        // get parametric angles
        ea0=ellipse_angle(rx,ry,a0);
        ea1=ellipse_angle(rx,ry,a1);
        // render elliptic arc
        glBegin(GL_LINE_STRIP);
        glColor3f(0.3,0.3,1.0);
        for (a=ea0,da=(ea1-ea0)/float(n-1),i=0;i<n;i++,a+=da)
            {
            x=rx*cos(a);
            y=ry*sin(a);
            glVertex2f(x,y);
            }
        glEnd();
        // render geometric axises (for visual check)
        glBegin(GL_LINE_STRIP);
        glColor3f(0.3,0.3,0.0);
        glVertex2f(2.0*cos(a0),2.0*sin(a0));
        glVertex2f(0.0,0.0);
        glVertex2f(2.0*cos(a1),2.0*sin(a1));
        glEnd();
        }

    glFlush();
    SwapBuffers(hdc);
    }
//---------------------------------------------------------------------------

where xs,ys is the resolution of my OpenGL window and M_PI=3.1415926535897932384626433832795 note all angles are in radians.

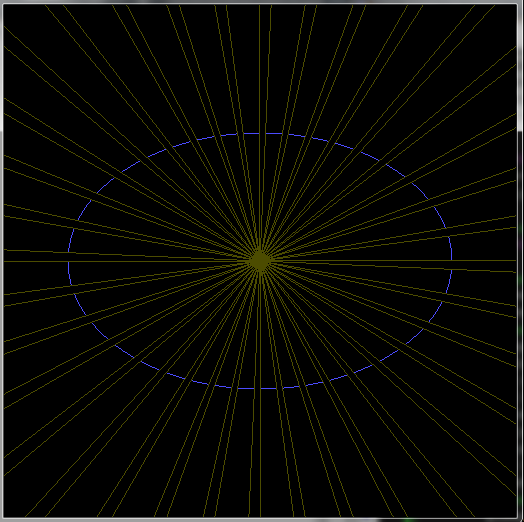
Here preview:

As you can see the angles match on the whole circumference (blue arcs align with yellow lines) ...

The function float ellipse_angle(float rx,float ry,float ang) will return elliptic parametric angle that corresponds to geometric angle ang on axis aligned ellipse with half axises rx,ry.

There are quite a few things that can improve speed of this like using rx/ry and scaling just one axis, precompute the angle constants etc.

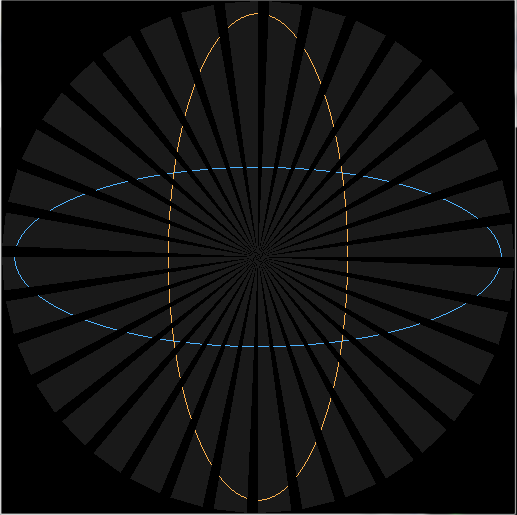
[Edit1] slightly better code

using aspect ratio and render is changed too for better visual check

//---------------------------------------------------------------------------
const float pi2=2.0*M_PI;
const float deg=M_PI/180.0;
//---------------------------------------------------------------------------
float ellipse_angle(float rx,float ry,float ang)    // geometrical angle [rad] -> ellipse parametric angle [rad]
    {
    float da,ea,ga,aspect;
    aspect=rx/ry;                                   // aspect ratio for speed up
    ang=fmod(ang,pi2);                              // normalize to <0,pi2>
    ea=ang;                                         // start elliptic angle
    ga=atan2(sin(ea),aspect*cos(ea));               // compute geometrical angle from it
    if (ga<0.0) ga+=pi2;                            // normalize to <0,pi2>
    if (ga<=ang)                                    // ea >= ang
        {
        da=90.0*deg-fmod(ang,90.0*deg);             // range to search
        da*=0.5;
        for (ea=ang;da>1e-10;da*=0.5)               // binary search
            {
            ea+=da;                                 // test next elliptic angle
            ga=atan2(sin(ea),aspect*cos(ea));       // compute geometrical angle from it
            if (ga<0.0) ga+=pi2;                    // normalize to <0,pi2>
            if (ga>ang) ea-=da;                     // restore original angle if too big
            }
        }
    else{                                           // ea <= ang
        da=fmod(ang,90.0*deg);                      // range to search
        da*=0.5;
        for (ea=ang;da>1e-10;da*=0.5)               // binary search
            {
            ea-=da;                                 // test next elliptic angle
            ga=atan2(sin(ea),aspect*cos(ea));       // compute geometrical angle from it
            if (ga<0.0) ga+=pi2;                    // normalize to <0,pi2>
            if (ga<ang) ea+=da;                     // restore original angle if too small
            }
        }
    return ea;
    }
//---------------------------------------------------------------------------
void gl_draw()
    {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    glScalef(1.0,float(xs)/float(ys),1.0);
    glMatrixMode(GL_TEXTURE);
    glLoadIdentity();
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    glDisable(GL_DEPTH_TEST);

    int i,n=100;
    float rx=0.95,ry=0.35;
    float x,y,a,dd,da,a0,a1,ea0,ea1;

    // test whole circumference
    for (dd=10.0*deg,a0=0.0,a1=a0+0.75*dd;a1<pi2;a0+=dd,a1+=dd)
        {
        // render geometric angle pies (for visual check)
        glBegin(GL_TRIANGLES);
        glColor3f(0.1,0.1,0.1);
        glVertex2f(cos(a0),sin(a0));
        glVertex2f(0.0,0.0);
        glVertex2f(cos(a1),sin(a1));
        glEnd();

        // get parametric angles (rx,ry)
        ea0=ellipse_angle(rx,ry,a0);
        ea1=ellipse_angle(rx,ry,a1);
        // render elliptic arc (rx,ry)
        glBegin(GL_LINE_STRIP);
        glColor3f(0.3,0.7,1.0);
        for (a=ea0,da=(ea1-ea0)/float(n-1),i=0;i<n;i++,a+=da)
            {
            x=rx*cos(a);
            y=ry*sin(a);
            glVertex2f(x,y);
            }
        glEnd();

        // get parametric angles (ry,rx)
        ea0=ellipse_angle(ry,rx,a0);
        ea1=ellipse_angle(ry,rx,a1);
        // render elliptic arc (ry,rx)
        glBegin(GL_LINE_STRIP);
        glColor3f(1.0,0.7,0.3);
        for (a=ea0,da=(ea1-ea0)/float(n-1),i=0;i<n;i++,a+=da)
            {
            x=ry*cos(a);
            y=rx*sin(a);
            glVertex2f(x,y);
            }
        glEnd();
        }

    glFlush();
    SwapBuffers(hdc);
    }
//---------------------------------------------------------------------------

There still room for improvement like get rid of atan2 completely and use cross product instead like I did in here:

• Generate a "pieslice" in C

[Edit2] Fast analytic O(1) solution

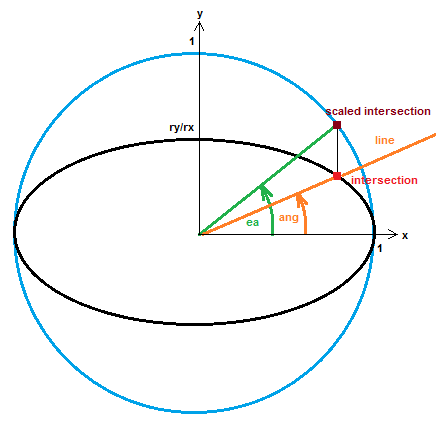
I simply used parametric line equation:

x(t) = t*cos(ang)
y(t) = t*sin(ang)

and implicit ellipse equation:

(x/rx)^2 + (y/ry)^2 = 1

to compute the intersection point (solve t and compute x,y from it), then apply inverse distortion on it to map from ellipse to circle (by scaling y*=rx/ry) and finally compute its angle with atan2(y,x).

Here C++ code:

//---------------------------------------------------------------------------
const float pi2=2.0*M_PI;
const float deg=M_PI/180.0;
//---------------------------------------------------------------------------
float ellipse_angle(float rx,float ry,float ang)    // geometrical angle [rad] -> ellipse parametric angle [rad]
    {
    float x,y,t,aa,bb,ea;
    x=cos(ang);                                     // axis direction at angle ang
    y=sin(ang);
    aa=rx*rx; bb=ry*ry;                             // intersection between ellipse and axis
    t=aa*bb/((x*x*bb)+(y*y*aa));
    x*=t; y*=t;
    y*=rx/ry;                                       // convert to circle
    ea=atan2(y,x);                                  // compute elliptic angle
    if (ea<0.0) ea+=pi2;                            // normalize to <0,pi2>
    return ea;
    }
//---------------------------------------------------------------------------

Amharic

well, I tried your example, but it doesn't seem to quite work as intended. Had to change C++ to C# and comennted out function calls that I already call elsewhere, and here is what I'm left with - pastebin.com/w0602xmN or a picture - imgur.com/a/uQFCGqJ – Kappel

thank you so much for your help, I have been struggling with this problem for several days before posting here, browsing all the similar answers but they never yielded such great results :) also the scaling with rx/ry works great too. As for fmod(), number1 % number2 works fine as C# replacement for fmod(), not quite sure why it didn't before. – Kappel

I was tinkering a little with your code, basically trying to add a proper way to set start/end angle of ellipse, from my understanding if I change initial for-loop in yours draw() to for(dd = 0.1 * deg, a0 = ellipseAngleBeggining a1 = ellipseAngleBeggining + 1*dd; a1 <= ellipseAngleEnd; a0 += dd, a1 += dd), I think I roughly get the results that I expect, but it really tanks the performance. Setting the dd =10 like you had initially leaves me unable to draw angles like 0.1 degree (with for loop above). Well, I assume doing the list of all of the results can help.. any ideas? – Kappel

@Kappel da is angle delta in radians and its usually enough to have 36-100 points per circumference so you can set for example da=3.1415926535897932384626433832795/100.0 ... however then you have to limit the last increment so that angle is not crossing end angel. Anyway beware dd is the first loop which renders n elliptic arcs instead o single one ... its just for testing whole circumference if the math is correct you can get rid of the outer loop completely and use just the inner one ... – Amharic

@Kappel You can also compute da from size of arc... for example: da=1.0 + floor(50.0*fabs(ea1-ea2)/3.1415926535897932384626433832795); da=3.1415926535897932384626433832795/da however if extreme eccentricities are used then you need more than 50.0 points per half ellipse. If you still hiting low performance then precompute your rendered geometry into array once (or on change) and use that (you can also use VBO to boost performance hugely in this way) because any non GL code inside glBegin/glEnd is a problem and as we are calling goniometrics and have branches inside its really bad – Amharic

@Kappel also hope you are calling ellipse_angle outside rendering loop just for the ea0,ea1 and not inside as its really slow O(log(n)) with goniometrics ... atan2 is worst I think. – Amharic

@Kappel see [Edit2] I come up with fast O(1) solution was afraid it would lead to system of quadratic transcendental equations but no its simple linear equation with single unknown instead :)... I also cleared out obsolete comments – Amharic