presenting motion of random walkers in matlab

Question

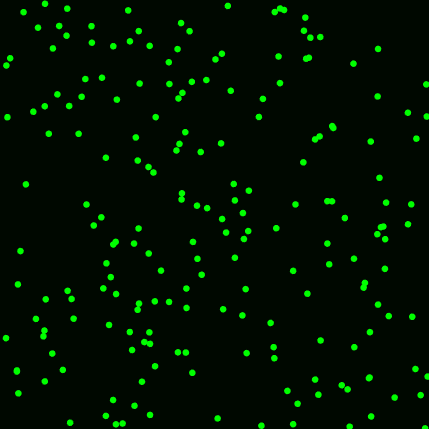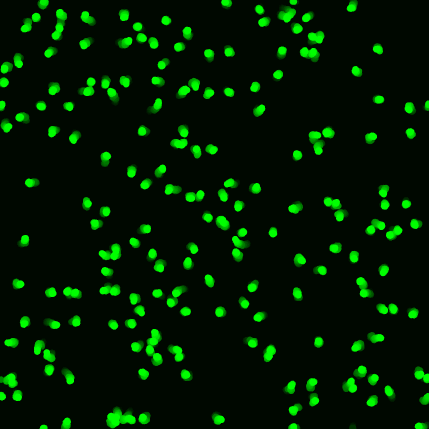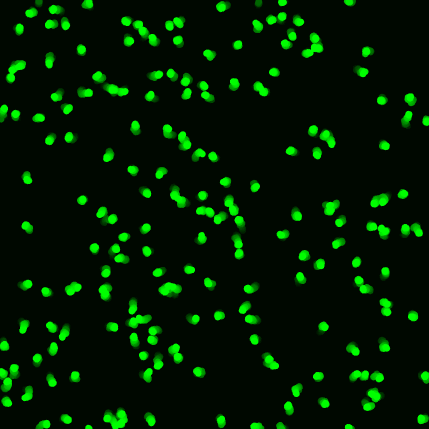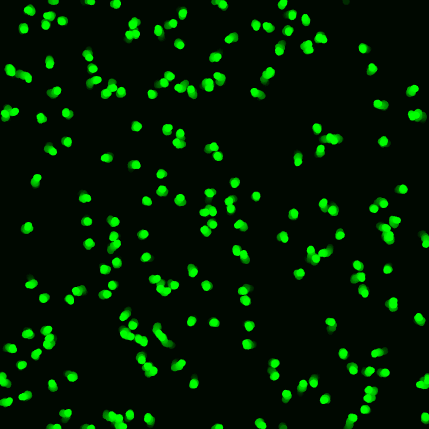
I have simulated some random walkers. I used

plot(xb,yb,'b--o')

to show particles in each step. I saw a code in below link with beautiful particles with tail which moves in a blur way. Is there a way which I could my random walkers the same as the walkers in the link in mat lab? Could anyone tell me which should I use instead of the plot function I used?

beautiful particles

The code I tried:

clear all
close all
lbox=20;

%random fluctuation 
eta = (2.*pi).*.1;
vs=0.02;
n=200;
birdl=[1:n];


axis([0 lbox 0 lbox])
axis('square')
hold on
xb=rand(n,1).*lbox;  %first possition
yb=rand(n,1).*lbox;    %first possition
vxb = 1;
vyb = 1;

for steps=1:5000;
xb = xb + vxb;
yb = yb+ vyb;

for bird1 = 1:n;
%periodic boundary condition
if(xb(bird1)<0);xb(bird1)=xb(bird1)+lbox; end
if (yb(bird1)<0);yb(bird1)=yb(bird1)+lbox;end
if (xb(bird1)>lbox);xb(bird1)=xb(bird1)-lbox;end
if (yb(bird1)>lbox);yb(bird1)=yb(bird1)-lbox;end

end
ang=eta.*(rand(n,1)-0.5);

vxb = vs.*cos(ang);
vyb = vs.*sin(ang);

cla

set(gcf,'doublebuffer','on')

plot(xb,yb,'.b')
%quiver(xb,yb,vxb,vyb,'b')
drawnow
end

Bedder

#42436193 – Sigridsigsmond

Answer 1

If you want to create a sort of trail of where the particles have recently been, you can store the previous nStore plots and change their color so that older plots gradually darken and fade to black (alpha transparency like in your sample isn't possible with line objects in MATLAB). Here's a reworking of your code (with a few other improvements, like replacing the inner boundary condition loop with indexing):

clear all
close all
lbox = 20;

%random fluctuation 
eta = (2.*pi).*1;
vs = 0.05;
n = 200;

set(gcf, 'doublebuffer', 'on', 'Color', 'k');
set(gca, 'Visible', 'off');
axis([0 lbox 0 lbox])
axis('square')
hold on
xb = rand(n, 1).*lbox;  %first possition
yb = rand(n, 1).*lbox;  %first possition
vxb = 1;
vyb = 1;

hList = [];
nStore = 30;
cMap = [zeros(nStore+1, 1) linspace(1, 0, nStore+1).' zeros(nStore+1, 1)];

for steps = 1:200

  xb = xb + vxb;
  yb = yb + vyb;

  %periodic boundary condition
  index = (xb < 0);
  xb(index) = xb(index) + lbox;
  index = (yb < 0);
  yb(index) = yb(index) + lbox;
  index = (xb > lbox);
  xb(index) = xb(index) - lbox;
  index = (yb > lbox);
  yb(index) = yb(index) - lbox;

  ang = eta.*(rand(n,1)-0.5);

  vxb = vs.*cos(ang);
  vyb = vs.*sin(ang);

  h = plot(xb, yb, '.g', 'MarkerSize', 12);
  if (numel(hList) == nStore)
    delete(hList(nStore));
    hList = [h hList(1:end-1)];
  else
    hList = [h hList];
  end

  set(hList, {'Color'}, num2cell(cMap(1:numel(hList), :), 2));

  drawnow
end

And here's an animation:

I created the animation by adding the following code:

% After the drawnow...
frame = getframe(gca);
im = frame2im(frame);
imind(:, :, 1, steps) = uint8(rgb2ind(im, cMap, 'nodither'));

% After the loop...
imwrite(imind(:, :, 1, 1:2:end), cMap, 'randwalk.gif', ...
        'Loopcount', Inf, 'DelayTime', 0);

I had to trim out some frames to make the gif smaller.

Robinia

Answer 2

My shot at "nicer" random walk:

clear all
close all
lbox=20;

figure('Color',[0 0 0])

%random fluctuation
eta = (2.*pi).*1;
vs=0.02;
n=300;
birdl=[1:n];


axis([0 lbox 0 lbox])
axis('square')
hold on
xb=rand(n,1).*lbox;  %first possition
yb=rand(n,1).*lbox;    %first possition
vxb = 1;
vyb = 1;

for steps=1:5000;
    xb = xb + vxb;
    yb = yb+ vyb;

    for bird1 = 1:n;
        %periodic boundary condition
        if (xb(bird1)<0);xb(bird1)=xb(bird1)+lbox; end
        if (yb(bird1)<0);yb(bird1)=yb(bird1)+lbox;end
        if (xb(bird1)>lbox);xb(bird1)=xb(bird1)-lbox;end
        if (yb(bird1)>lbox);yb(bird1)=yb(bird1)-lbox;end

    end
    ang=eta.*(rand(n,1)-0.5);

    vxb = vs.*cos(ang);
    vyb = vs.*sin(ang);

    cla
    set(gca,'Color',[0 0 0]);
    set(gcf,'doublebuffer','on')
    set(gca,'YTick',[]);
    set(gca,'XTick',[]);

    plot(xb,yb,'.g','markersize',10)
    % this should draw lines, but its slow and not as neat as a web app
%     plot([xb xb-vxb*5]',[yb yb-vyb*5]','g') 

    drawnow
end

Sigridsigsmond

@oliverrouph MATLAB is not the tool for graphics, but scientific computing. Still, if you take the time to read the code, you can see that I added a rough approach for a tail. Modify as pleased to make that tail nicer. – Sigridsigsmond

@oliverrouph Actually if you uncomment the code you will see the same tails as in the webpage. – Sigridsigsmond