General method for calculating Smooth vertex normals with 100% smoothness

Question

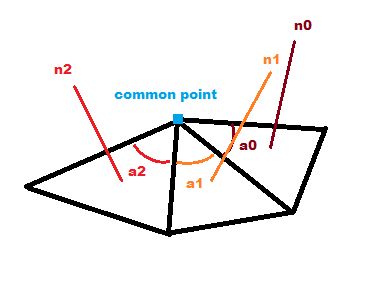
I've looked online for quite some time and can't find an answer to this. For simplicity, let's just assume I need to fully smooth out the normals of a group of cojoined faces. I want to find the actual geometric bisector between a group of vectors, ignoring duplicate normals and maintaining accuracy with triangle soups. Basically, it needs to:

• Work with triangle soups - be it three, 4 or 4000 triangles, the normals still need to work together in a geometrically correct fashion without being biased towards arbitrary areas
• Ignore overlapping (parallel) normals - if I have a cube's edge that comes together in 3 triangles, or one that comes together in one triangle for each of two sides and 2 (or more) for the last side, or one that has a million triangles on only one side, the bisector must not change

The most common formula I seem to be finding for normal smoothing is, to simply average them by summing together the normal vectors and divide by three; example:

normalize((A + B + C) / 3);

Of course dividing by three is useless, which already denotes the vibe of naive, off-the-top-of-your-head brute force averaging method that people propose; problems with this are also the fact that it messes up big time with even triangle soups and parallel normals.

Another remark I seem to find is to keep the initial "facet" normals as they come from a common cross multiply operation that generates them, as that way they are (kinda) weighted against the triangle's area. This might be something you want to do in some cases, however I need the pure bisector, so area must not influence the formula, and even accounting for it it still gets messed up by triangle soups.

I saw one mentioned method that says to weight against the angle between the adjacent faces, but I can't seem to implement the formula correctly - either that or it's not doing what I want. However that's hard for me to say, since I can't find a concise explanation for it and my mind is becoming numb from all this wasted brainstorming.

Anybody knows of a general formula? If it is of any help, I'm working with C++ and DirectX11.

---

Edit: Here's some similar questions that describe some of the methods;

• How to achieve smooth tangent space normals?
• Calculating Vertex Normals of a mesh
• Calculating normals in a triangle mesh
• How does Blender calculate vertex normals?
• Most efficient algorithm to calculate vertex normals from set of triangles for Gouraud shading

Also this article: http://www.bytehazard.com/articles/vertnorm.html

Unfortunately, the implementations I tried didn't work and I couldn't find a clear, concise statement about which formula was actually the one that I needed. After some trial and error I finally figured out that weighting by angle was the correct way to do it, only I wasn't able to implement it correctly; as it seems to be working now, I'll add my implementation as an answer below.

Sorel

Can you show your attempt at coding the weighting algorithm? Could be a simple algebraic mistake, but otherwise the method sounds... sound. – Ashmore

Possible duplicate of How to achieve smooth tangent space normals? – Peg

Ok, while I was collecting data and rewriting the functions I had used to show (many different attempts with many structures, which I had deleted since I was set on holding on until I could find a rigorous formula from an answer, and then apply it in practice) I regained a moment of brain activity and understood what the angle weighting was supposed to be. I've done some tests and it seems to be working; will post more details along with a proper, detailed answer after I get some sleep. – Sorel

@Peg there are actually a lot of questions I've seen on the website and on others as well, pertaining to this problem; while 99% of them stopped after a "just average the vectors" answer, even the ones that explained other methods didn't seem to be working for me or just weren't clear enough. If I'm allowed, I would like to post here my results and clarify the dilemma for whomever else might need it in the future. – Sorel

@Sorel yes you are allowed to answer your own questions on SO... – Peg

@Peg I know. I was referring to having the question left open and not closed as duplicate. Though I guess in case I could add my answer to other questions too. – Sorel

Answer 1

The correct method is to weight the "facet" normals against the angle between the two neighbor vertices of the one shared in the edge/corner.

(here shown the angle with respect to each face)

Here's a rundown of an example implementation:

for (int f = 0; f < tricount; f++)
{
    // ...
    // p1, p2 and p3 are the points in the face (f)

    // calculate facet normal of the triangle using cross product;
    // both components are "normalized" against a common point chosen as the base
    float3 n = (p2 - p1).Cross(p3 - p1);    // p1 is the 'base' here

    // get the angle between the two other points for each point;
    // the starting point will be the 'base' and the two adjacent points will be normalized against it
    a1 = (p2 - p1).Angle(p3 - p1);    // p1 is the 'base' here
    a2 = (p3 - p2).Angle(p1 - p2);    // p2 is the 'base' here
    a3 = (p1 - p3).Angle(p2 - p3);    // p3 is the 'base' here

    // normalize the initial facet normals if you want to ignore surface area
    if (!area_weighting)
    {
        normalize(n);
    }

    // store the weighted normal in an structured array
    v1.wnormals.push_back(n * a1);
    v2.wnormals.push_back(n * a2);
    v3.wnormals.push_back(n * a3);
}
for (int v = 0; v < vertcount; v++)
{
    float3 N;

    // run through the normals in each vertex's array and interpolate them
    // vertex(v) here fetches the data of the vertex at index 'v'
    for (int n = 0; n < vertex(v).wnormals.size(); v++)
    {
        N += vertex(v).wnormals.at(n);
    }

    // normalize the final normal
    normalize(N);
}

Here's an example of a "naive" average of the normals (i.e. without angle weighting);

You can see the facet components being all the same, but since some sides have two faces, their part of the interpolation is doubled, making the average skewed. Weighting only against the surface area, but not the angles, produces similar results.

This is instead the same model, but with angle weighting enabled;

Now the interpolated normals are all geometrically correct.

Sorel

may be I am missing something but if p1,p2,p3 are the vertexes of the same triangle (face) then all the normals n1,n2,n3 are the same. So the whole code is just making nonsense computations agregating 180 deg angle to the sum of normals and then normalizing again to original normal. To make this work you would need to compute just single normal per face and add the weighted normal and weight to each per vertex normal structure just like in the duplicate link. The difference is you will not increment counter but add the weight to it. – Peg

Also angles as weight does not seem as a "best" choice to me (unless it is a angle of face between vertices of face and common point between different faces) I would chose triangle area as weight instead which is directly computed as un-normalized normal size from the cross product. – Peg

@Peg You are exactly right about the counter, my bad; I will edit the post. About the surface area however, it doesn't work since all the triangles have the same area. – Sorel

@Peg unless it is a angle of face between vertices of face and common point between different faces - I'm not sure I see what you mean, could you elaborate on this one? – Sorel

added image to your answer – Peg

a1 = (p2 - p1).Angle(p3 - p1); // p1 is the 'base' here this is the angle between p2 and p3 with respect to shared vertex p1; the other two lines are the same, only for the other vertices. Also thanks for the image, if you don't mind I'll use it in the header to show the concept more clearly – Sorel

I see it now v1.wnormals.push_back(n * a1) ... you got list of shared normals on per vertex basis why not sum directly instead (so you would need just accumulator normal instead of list? Yes you can use the image I just sketch it in paint – Peg

Because you do not have direct access to all the normals acting on a shared vertex until you finish the loop; you can keep just the sum and discard the others, but then you'll lose the benefit of the structured array that lets you have all the single facet normals for future usage. Mathematically it would work perfectly of course, so that's up to the needs of who implements it – Sorel