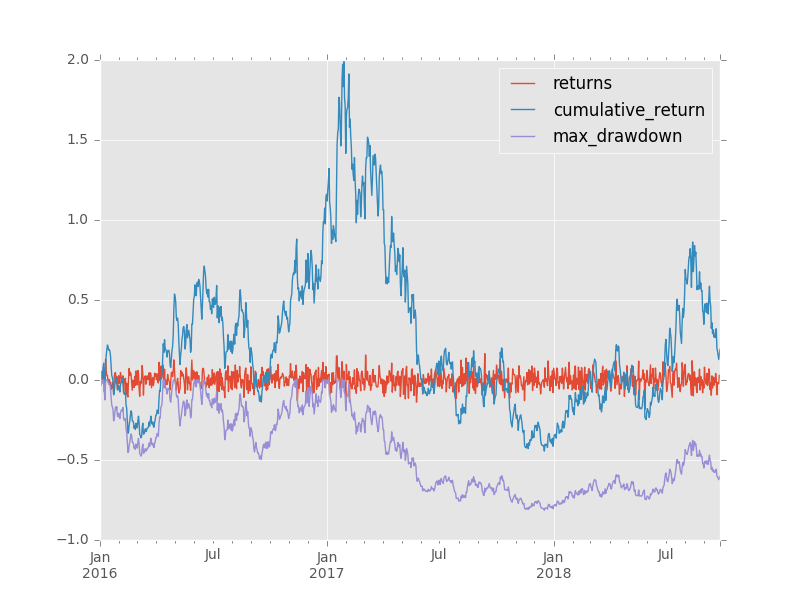
Given a time series of returns, we need to evaluate the aggregate return for every combination of starting point to ending point.
The first trick is to convert a time series of returns into a series of return indices. Given a series of return indices, I can calculate the return over any sub-period with the return index at the beginning ri_0 and at the end ri_1. The calculation is: ri_1 / ri_0 - 1.
The second trick is to produce a second series of inverses of return indices. If r is my series of return indices then 1 / r is my series of inverses.
The third trick is to take the matrix product of r * (1 / r).Transpose.
r is an n x 1 matrix. (1 / r).Transpose is a 1 x n matrix. The resulting product contains every combination of ri_j / ri_k. Just subtract 1 and I've actually got returns.
The fourth trick is to ensure that I'm constraining my denominator to represent periods prior to those being represented by the numerator.
Below is my vectorized function.
import numpy as np
import pandas as pd
def max_dd(returns):
# make into a DataFrame so that it is a 2-dimensional
# matrix such that I can perform an nx1 by 1xn matrix
# multiplication and end up with an nxn matrix
r = pd.DataFrame(returns).add(1).cumprod()
# I copy r.T to ensure r's index is not the same
# object as 1 / r.T's columns object
x = r.dot(1 / r.T.copy()) - 1
x.columns.name, x.index.name = 'start', 'end'
# let's make sure we only calculate a return when start
# is less than end.
y = x.stack().reset_index()
y = y[y.start < y.end]
# my choice is to return the periods and the actual max
# draw down
z = y.set_index(['start', 'end']).iloc[:, 0]
return z.min(), z.argmin()[0], z.argmin()[1]
How does this perform?
for the vectorized solution I ran 10 iterations over the time series of lengths [10, 50, 100, 150, 200]. The time it took is below:
10: 0.032 seconds
50: 0.044 seconds
100: 0.055 seconds
150: 0.082 seconds
200: 0.047 seconds
The same test for the looped solution is below:
10: 0.153 seconds
50: 3.169 seconds
100: 12.355 seconds
150: 27.756 seconds
200: 49.726 seconds
Edit
Alexander's answer provides superior results. Same test using modified code
10: 0.000 seconds
50: 0.000 seconds
100: 0.004 seconds
150: 0.007 seconds
200: 0.008 seconds
I modified his code into the following function:
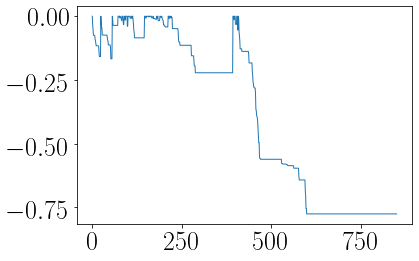
def max_dd(returns):
r = returns.add(1).cumprod()
dd = r.div(r.cummax()).sub(1)
mdd = drawdown.min()
end = drawdown.argmin()
start = r.loc[:end].argmax()
return mdd, start, end

r.loc[:end].argmax()will give you an issue here. You wantr.loc[:end].sort_index(ascending=False).argmax(). If you have multiple zeros in your Series (multiple high water marks), the current line as-is will return the first rather than last occurrence and yield a start date that's way too early. – Bordereau.sort_index(ascending=False)to reverse the Series would incorrectly tell you your drawdown started in Jan. I guess it's interpretation, but under that method wouldn't every drawdown start at month 0 or month 1? I've never seen the start date described as such. The HWMs don't have to be identical to get multiple zeros in your drawdown series. – Bordereau