Start, End and Duration of Maximum Drawdown in Python

Question

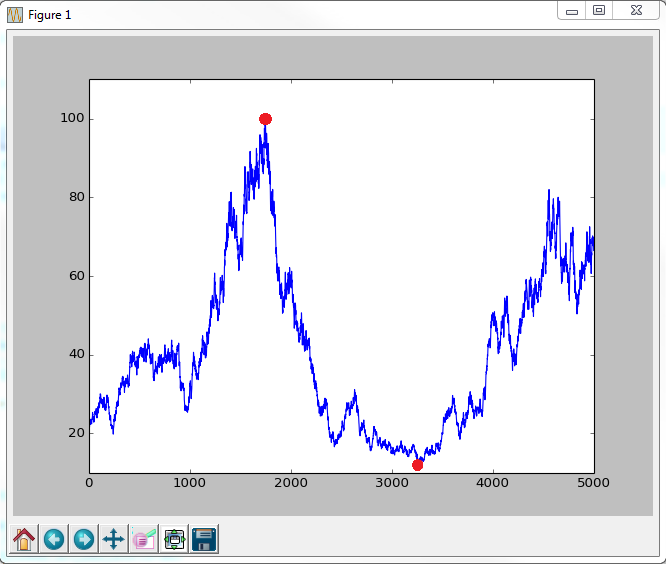
Given a time series, I want to calculate the maximum drawdown, and I also want to locate the beginning and end points of the maximum drawdown so I can calculate the duration. I want to mark the beginning and end of the drawdown on a plot of the timeseries like this:

So far I've got code to generate a random time series, and I've got code to calculate the max drawdown. If anyone knows how to identify the places where the drawdown begins and ends, I'd really appreciate it!

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

# create random walk which I want to calculate maximum drawdown for:

T = 50
mu = 0.05
sigma = 0.2
S0 = 20
dt = 0.01
N = round(T/dt)
t = np.linspace(0, T, N)
W = np.random.standard_normal(size = N) 
W = np.cumsum(W)*np.sqrt(dt) ### standard brownian motion ###
X = (mu-0.5*sigma**2)*t + sigma*W 

S = S0*np.exp(X) ### geometric brownian motion ###
plt.plot(S)

# Max drawdown function      

def max_drawdown(X):
    mdd = 0
    peak = X[0]
    for x in X:
        if x > peak: 
            peak = x
        dd = (peak - x) / peak
        if dd > mdd:
            mdd = dd
    return mdd    

drawSeries = max_drawdown(S)
MaxDD = abs(drawSeries.min()*100)
print MaxDD


plt.show()

Unwonted

You might be interested in this: #21058833 – Ureter

There's a similar question here that has a useful answer (for pandas though): quant.stackexchange.com/questions/55130/… – Populace

Answer 1

Just find out where running maximum minus current value is largest:

n = 1000
xs = np.random.randn(n).cumsum()
i = np.argmax(np.maximum.accumulate(xs) - xs) # end of the period
j = np.argmax(xs[:i]) # start of period

plt.plot(xs)
plt.plot([i, j], [xs[i], xs[j]], 'o', color='Red', markersize=10)

Professorship

Really clean solution to maximum drawdown! – Unwonted

if u dun mind, can you explain the code for i and j? – Tandie

For i: np.maximum.accumulate(xs) gives us the cumulative maximum. Taking the difference between that and xs and finding the argmax of that gives us the location where the cumulative drawdown is maximized. Then for j: xs[:i] takes all the points from the start of the period until point i, where the max drawdown concludes. np.argmax(xs[:i]) finds the location/index of the highest (maximum) point in the graph up till that point, so that is the peak we are looking for. – Structuralism

This method throws an error if there is no drawdown (all points are higher than previous). It should be checked if the i == 0 and if that is true, drawdown is also 0 – Quitrent

Could you please show how to add real "date" to the x-axis of this drawdown plot? So far the code works but only works with numpy arrays.What if the time series comes in a fashion of pandas series with timestamps as the index? In other words, it'd be really nice to show real date on a plot so you have a sense of the timeframe in which you look at things. Thank you! – Amalea

I think this solution does not work properly when drawdown starts at the very beginning. If we take xs to [-0.1008311 , -0.07035855, 0.07000701, 0.00107728, -0.02935416, -0.0148309 , -0.07025561, -0.15400001, 0.01393718, 0.06848435] then the maximal DD is -0.36 but this approach gives -0.26 – Lavine

@Lavine indeed this solution only gets the last drawdown and not the max duration draw down. – Styracaceous

@Styracaceous I am not sure I am able to produce an example confirming your claim (last drawdown) . Could you give one? – Lavine

@Lavine it's a lot of code and need the data too .. so sorry can't do. What I can do is to post my own solution which is not as beautiful but it's tested and works. – Styracaceous

Answer 2

behzad.nouri solution is very clean, but it's not a maximum drawdow (couldn't comment as I just opened my account and I don't have enough reputation atm).

What you end up having is the maximum drop in the nominal value rather than a relative drop in value (percentage drop). For example, if you would apply this to time series that is ascending over the long run (for example stock market index S&P 500), the most recent drop in value (higher nominal value drops) will be prioritized over the older decrease in value as long as the drop in nominal value/points is higher.

For example S&P 500:

• 2007-08 financial crisis, drop 56.7%, 888.62 points
• Recent Corona Virus crisis, drop 33.9%, 1,1148.75 points

By applying this method to period after 2000, you'll see Corona Virus Crisis rather than 2007-08 Financial Crisis

Related code (from behzad.nouri) below:

n = 1000
xs = np.random.randn(n).cumsum()
i = np.argmax(np.maximum.accumulate(xs) - xs) # end of the period
j = np.argmax(xs[:i]) # start of period

plt.plot(xs)
plt.plot([i, j], [xs[i], xs[j]], 'o', color='Red', markersize=10)

You just need to divide this drop in nominal value by the maximum accumulated amount to get the relative ( % ) drawdown.

( np.maximum.accumulate(xs) - xs ) / np.maximum.accumulate(xs)

Toluidine

Answer 3

on the back of this I added unerwater analysis if that helps anyone...

def drawdowns(equity_curve):
    i = np.argmax(np.maximum.accumulate(equity_curve.values) - equity_curve.values) # end of the period
    j = np.argmax(equity_curve.values[:i]) # start of period

    drawdown=abs(100.0*(equity_curve[i]-equity_curve[j]))

    DT=equity_curve.index.values

    start_dt=pd.to_datetime(str(DT[j]))
    MDD_start=start_dt.strftime ("%Y-%m-%d") 

    end_dt=pd.to_datetime(str(DT[i]))
    MDD_end=end_dt.strftime ("%Y-%m-%d") 

    NOW=pd.to_datetime(str(DT[-1]))
    NOW=NOW.strftime ("%Y-%m-%d")

    MDD_duration=np.busday_count(MDD_start, MDD_end)

    try:
        UW_dt=equity_curve[i:].loc[equity_curve[i:].values>=equity_curve[j]].index.values[0]
        UW_dt=pd.to_datetime(str(UW_dt))
        UW_dt=UW_dt.strftime ("%Y-%m-%d")
        UW_duration=np.busday_count(MDD_end, UW_dt)
    except:
        UW_dt="0000-00-00"
        UW_duration=np.busday_count(MDD_end, NOW)

    return MDD_start, MDD_end, MDD_duration, drawdown, UW_dt, UW_duration

Adulteress

Answer 4

Your max_drawdown already keeps track of the peak location. Modify the if to also store the end location mdd_end when it stores mdd, and return mdd, peak, mdd_end.

Quadriplegia

Answer 5

I agree with k0rnik.

A short example for prooving that formula given by behzad.nouri can produce wrong result.

xs = [1, 50, 10, 180, 40, 200]

pos_min1 = np.argmax(np.maximum.accumulate(xs) - xs) # end of the period
pos_peak1 = np.argmax(xs[:pos_min1]) # start of period

pos_min2 = np.argmax((np.maximum.accumulate(xs) - 
xs)/np.maximum.accumulate(xs)) # end of the period
pos_peak2 = np.argmax(xs[:pos_min2]) # start of period

plt.plot(xs)
plt.plot([pos_min1, pos_peak1], [xs[pos_min1], xs[pos_peak1]], 'o', 
label="mdd 1", color='Red', markersize=10)
plt.plot([pos_min2, pos_peak2], [xs[pos_min2], xs[pos_peak2]], 'o', 
label="mdd 2", color='Green', markersize=10)
plt.legend()

mdd1 = 100 * (xs[pos_min1] - xs[pos_peak1]) / xs[pos_peak1]
mdd2 = 100 * (xs[pos_min2] - xs[pos_peak2]) / xs[pos_peak2]

print(f"solution 1: peak {xs[pos_peak1]}, min {xs[pos_min1]}\n rate : 
{mdd1}\n")
print(f"solution 2: peak {xs[pos_peak2]}, min {xs[pos_min2]}\n rate : 
{mdd2}")

Further the price of an asset cannot be negative so

xs = np.random.randn(n).cumsum()

is not correct. It could be better to add:

xs -= (np.min(xs) - 10)

Ginder

Answer 6

This solution is tested and works but here I'm computing the maximum duration drawdown and NOT the duration of the maximum drawdown. The solution can be easily adapted to find the duration of the maximum drawdown.

def max_dur_drawdown(dfw, threshold=0.05):
    """
    Labels all drawdowns larger in absolute value than a threshold and returns the 
    drawdown of maximum duration (not the max drawdown necessarily but most often they
    coincide).
    
    Args:
        dfw (pd.DataFrame): monthly data, the pre-computed drawdowns or underwater.
        threshold (float): only look at drawdowns greater than this in absolute value e.g. 5%
        
    Returns:
        dictionary containing the start, end dates and duration in months for the maximum
        duration drawdowns keyed by column name.
    """
    max_dur_per_column = {}
    columns = dfw.columns.copy()
    mddd_start = {}
    mddd_end = {}
    mddd_duration = {}
    for col in columns:
        # run the drawdown labeling algorithm
        dfw['sign'] = 0
        dfw['sign'].loc[dfw[col] == 0] = +1
        dfw['sign'].loc[dfw[col] <  0] = -1
        # find the sign change data points
        dfw['change'] = dfw['sign'] != dfw['sign'].shift(1)
        # the first change doesn't count
        dfw['change'].iloc[0] = False
        # demarcate the lef and right of the drawdowns
        left = dfw[(dfw['change'] == True) & (dfw['sign'] == -1)].index.values
        right = dfw[(dfw['change'] == True) & (dfw['sign'] == 1)].index.values
        min_len = min(len(left), len(right))
        intervals = pd.IntervalIndex.from_arrays(left[0:min_len], right[0:min_len])
        # find the minimum value per drawdown interval so we label all data points to the left of it.
        min_per_int = list(map(lambda i: (i.left, i.right, dfw[col][(dfw.index >= i.left) & (dfw.index < i.right)].min()), intervals))
        # filter out drawdowns lower in absolute value than a threshold
        min_per_int = list(filter(None.__ne__, list(map(lambda x: None if x[2] >= -threshold else x, min_per_int))))
        # label only the negative part of the underwater NDD stands for negative-side drawdown.
        dfw['NDD'] = 0
        mddd_start[col] = None
        mddd_end[col] = None
        mddd_duration[col] = 0
        for i in min_per_int:
            # find the index of the data point that is minimum this is an argmin
            min_idx = dfw[(dfw.index >= i[0]) & (dfw.index < i[1]) & (abs(dfw[col] - i[2]) < 1e-15)].index[0]
            # compute the duration and update the maximum duration if needed
            tmp_dur = int(np.round((min_idx - i[0]) / np.timedelta64(1, 'M')))
            if tmp_dur > mddd_duration[col]:
                mddd_start[col] = i[0].date()
                mddd_end[col] = min_idx.date()
                mddd_duration[col] = tmp_dur

    return mddd_start, mddd_end, mddd_duration
    

Example usage:

# compute cumulative returns
dfc = pd.DataFrame(dfr['S&P500'] / dfr['S&P500'][0])

# compute drawdowns
dfw = dfc / dfc.cummax() - 1

print(max_dur_drawdown(dfw))

Styracaceous