Spline with constraints at border

Question

I have measured data on a three dimensional grid, e.g. f(x, y, t). I want to interpolate and smooth this data in the direction of t with splines. Currently, I do this with scipy.interpolate.UnivariateSpline:

import numpy as np
from scipy.interpolate import UnivariateSpline

# data is my measured data
# data.shape is (len(y), len(x), len(t))
data = np.arange(1000).reshape((5, 5, 40))  # just for demonstration
times = np.arange(data.shape[-1])
y = 3
x = 3
sp = UnivariateSpline(times, data[y, x], k=3, s=6)

However, I need the spline to have vanishing derivatives at t=0. Is there a way to enforce this constraint?

Flunk

It sounds like the following code may do what you need eqtools.readthedocs.org/en/latest/_modules/eqtools/… – Older

I made an edit to fix your example. Based on your saying what data.shape is, I think my edit matches your intent, but please review and revert if not. – Gratis

Answer 1

The best thing I can think of is to do a minimization with a constraint with scipy.optimize.minimize. It is pretty easy to take the derivative of a spline, so the constraint is simply. I would use a regular spline fit (UnivariateSpline) to get the knots (t), and hold the knots fixed (and degree k, of course), and vary the coefficients c. Maybe there is a way to vary the knot locations as well but I will leave that to you.

import numpy as np
from scipy.interpolate import UnivariateSpline, splev, splrep
from scipy.optimize import minimize

def guess(x, y, k, s, w=None):
    """Do an ordinary spline fit to provide knots"""
    return splrep(x, y, w, k=k, s=s)

def err(c, x, y, t, k, w=None):
    """The error function to minimize"""
    diff = y - splev(x, (t, c, k))
    if w is None:
        diff = np.einsum('...i,...i', diff, diff)
    else:
        diff = np.dot(diff*diff, w)
    return np.abs(diff)

def spline_neumann(x, y, k=3, s=0, w=None):
    t, c0, k = guess(x, y, k, s, w=w)
    x0 = x[0] # point at which zero slope is required
    con = {'type': 'eq',
           'fun': lambda c: splev(x0, (t, c, k), der=1),
           #'jac': lambda c: splev(x0, (t, c, k), der=2) # doesn't help, dunno why
           }
    opt = minimize(err, c0, (x, y, t, k, w), constraints=con)
    copt = opt.x
    return UnivariateSpline._from_tck((t, copt, k))

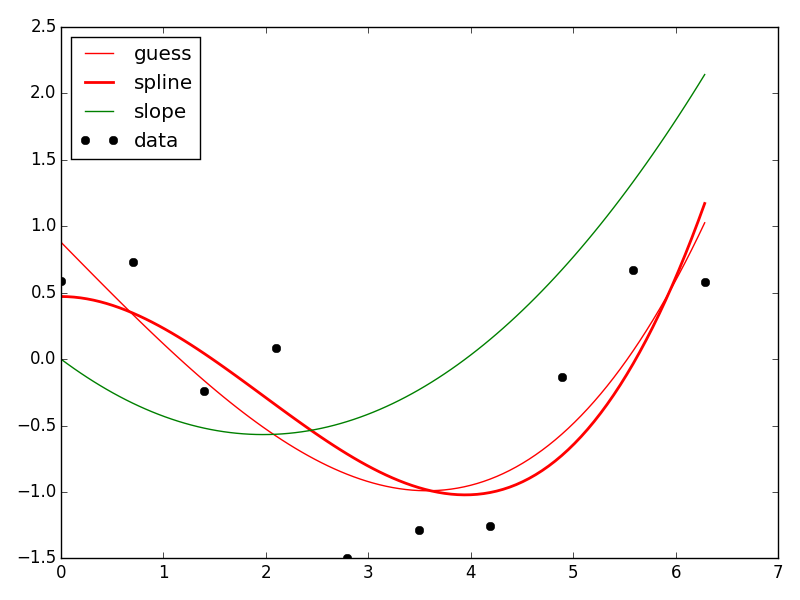
And then we generate some fake data that should have zero initial slope and test it:

import matplotlib.pyplot as plt

n = 10
x = np.linspace(0, 2*np.pi, n)
y0 = np.cos(x) # zero initial slope
std = 0.5
noise = np.random.normal(0, std, len(x))
y = y0 + noise
k = 3

sp0 = UnivariateSpline(x, y, k=k, s=n*std)
sp = spline_neumann(x, y, k, s=n*std)

plt.figure()
X = np.linspace(x.min(), x.max(), len(x)*10)
plt.plot(X, sp0(X), '-r', lw=1, label='guess')
plt.plot(X, sp(X), '-r', lw=2, label='spline')
plt.plot(X, sp.derivative()(X), '-g', label='slope')
plt.plot(x, y, 'ok', label='data')
plt.legend(loc='best')
plt.show()

Gratis

This looks very good, and it is probably the one answer that ensures a smooth spline that makes sense for all data points and the constraint. Accepted as answer and added the bounty. – Flunk

You may want to answer here – Cripps

The optimization method was not explicitly given. Is it SLSQP? – Blader

Answer 2

Here is one way to do this. The basic idea is to get a spline's coefficients with splrep and then modify them before calling splev. The first few knots in the spline correspond to the lowest value in the range of x values. If the coefficients that correspond to them are set equal to each other, that completely flattens out the spline at that end.

Using the same data, times, x, y as in your example:

# set up example data
data = np.arange(1000).reshape((5, 5, 40))
times = np.arange(data.shape[-1])
y = 3
x = 3

# make 1D spline
import scipy.interpolate
from pylab import * # for plotting
knots, coefficients, degree = scipy.interpolate.splrep(times, data[y, x])
t = linspace(0,3,100)
plot( t, scipy.interpolate.splev(t, (knots, coefficients, degree)) )

# flatten out the beginning
coefficients[:2] = coefficients[0]
plot( t, scipy.interpolate.splev(t, (knots, coefficients, degree)) )
scatter( times, data[y, x] )
xlim(0,3)
ylim(720,723)

Blue: original points and spline through them. Green: modified spline with derivative=0 at the beginning. Both are zoomed in to the very beginning.

plot( t, scipy.interpolate.splev(t, (knots, coefficients, degree), der=1), 'g' )
xlim(0,3)

Call splev(..., der=1) to plot the first derivative. The derivative starts at zero and overshoots a little so the modified spline can catch up (this is inevitable).

The modified spline does not go through the first two points it is based on (it still hits all the other points exactly). It is possible to modify this by adding an extra interior control point next to the origin to get both a zero derivative and go through the original points; experiment with the knots and coefficients until it does what you want.

Unsound

Good idea. And it is probably way faster than the minimization approach above. – Flunk

I suggest maybe prepending a new knot and new coefficient at the same values as the existing first knot and coefficient. I can't try it now, but this might be closer to the original fit. – Gratis

Answer 3

Your example does not work ( on python 2.7.9), so I only sketch my idea:

1. calculate sp
2. take the derivative via sp.derivative and evaluate it at the relevant times (probably the same times at which you measured your data)
3. Set the relevant points to zero (e.g. the value at t=0)
4. Calculate another spline from the derivative values.
5. Integrate your spline function. I guess you will have to do this numerically, but that should not be a problem. Do not forget to add a constant, to get your original function.

Arand

I guess one would need to do that iteratively until the spline converges to something smooth and meaningful... Since the actual data is near my constraint, it probably would not take that many iterations... Good idea! – Flunk