I found this section confusing on first reading too, and only started to get it after I'd read up elsewhere about continuations and continuation-passing style (which is what this is).
At the risk of explaining something that you already get, one way of looking at it that helped me is to think of the "collector" or "continuation" as replacing the normal way for the function to return values. In the normal style of programming, you call a function, receive a value, and do something with it in the caller. For example, the standard recursive length function includes the expression (+ 1 (length (cdr list))) for the non-empty case. That means that once (length (cdr list)) returns a value, there's a computation waiting to happen with whatever value it produces, which we could think of as (+ 1 [returned value]). In normal programming, the interpreter keeps track of these pending computations, which tend to "stack up", as you can see in the first couple of chapters of the book. For example, in calculating the length of a list recursively we have a nest of "waiting computations" as many levels deep as the list is long.
In continuation-passing style, instead of calling a function and using the returned result in the calling function, we tell the function what to do when it produces its value by providing it with a "continuation" to call. (This is similar to what you have to do with callbacks in asynchronous Javascript programming, for example: instead of writing result = someFunction(); you write someFunction(function (result) { ... }), and all of the code that uses result goes inside the callback function).
Here's length in continuation-passing style, just for comparison. I've called the continuation parameter return, which should suggest how it functions here, but remember that it's just a normal Scheme variable like any other. (Often the continuation parameter is called k in this style).
(define (length/k lis return)
(cond ((null? lis) (return 0))
(else
(length/k (cdr lis)
(lambda (cdr-len)
(return (+ cdr-len 1)))))))
There is a helpful tip for reading this kind of code in an article on continuations by Little Schemer co-author Dan Friedman. (See section II-5 beginning on page 8). Paraphrasing, here's what the else clause above says:
imagine you have the result of calling length/k on (cdr lis), and
call it cdr-len, then add one and pass the result of this addition
to your continuation (return).
Note that this is almost exactly what the interpreter has to do in evaluating (+ 1 (length (cdr lis))) in the normal version of the function (except that it doesn't have to give a name to the intermediate result (length (cdr lis)). By passing around the continuations or callbacks we've made the control flow (and the names of intermediate values) explicit, instead of having the interpreter keep track of it.
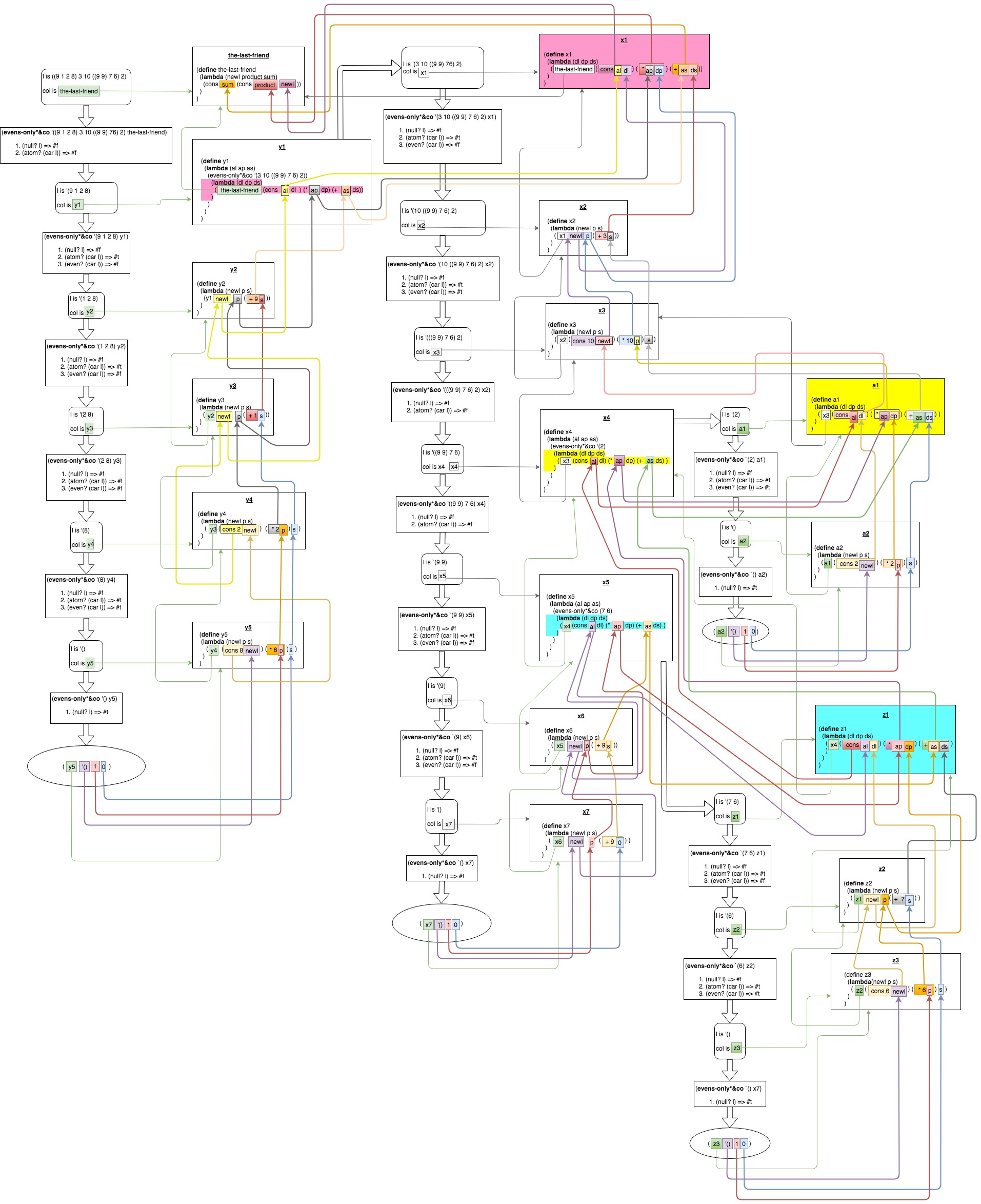
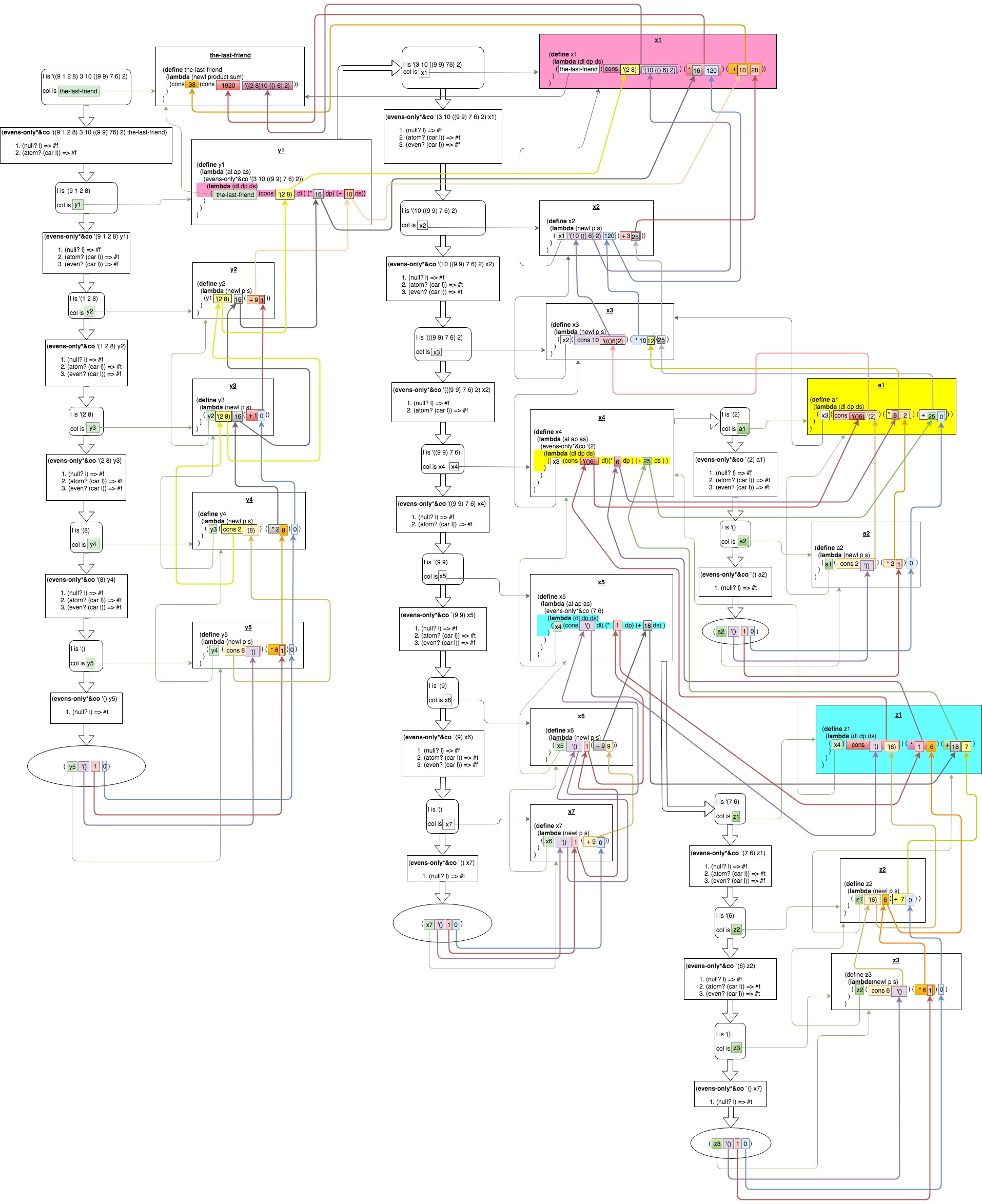
Let's apply this method to each clause in evens-only*&co. It's slightly complicated here by the fact that this function produces three values rather than one: the nested list with odd numbers removed; the product of the even numbers; and the sum of the odd numbers. Here's the first clause, where (car l) is known to be an even number:
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col (cons (car l) newl)
(opx (car l) product)
sum)))
Imagine that you have the results of removing odd numbers,
multiplying evens, and adding odd numbers from the cdr of the list,
and call them newl, product, and sum respectively. cons the
head of the list onto newl (since it's an even number, it should go
in the result); multiply product by the head of the list (since
we're calculating product of evens); leave sum alone; and pass these
three values to your waiting continuation col.
Here's the case where the head of the list is an odd number:
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col newl product (op+ (car l) sum))))
As before, but pass the same values of newl and product to the continuation (i.e. "return" them), along with the sum of sum and the head of the list, since we're summing up odd numbers.
And here's the last one, where (car l) is a nested list, and which is slightly complicated by the double recursion:
(evens-only*&co (car l)
(lambda (newl product sum)
(evens-only*&co (cdr l)
(lambda (dnewl dproduct dsum)
(col (cons newl dnewl)
(opx product dproduct)
(op+ sum dsum))))))
Imagine you have the results from removing, summing and adding the
numbers in (car l) and call these newl, product, and sum; then
imagine you have the results from doing the same thing to (cdr l),
and call them dnewl, dproduct and dsum. To your waiting
continuation, give the values produced by consing newl and dnewl
(since we're producing a list of lists); multiplying together
product and dproduct; and adding sum and dsum.
Notice: each time we make a recursive call, we construct a new continuation for the recursive call, which "closes over" the current values of the argument, l, and the return continuation - col, in other words, you can think of the chain of continuations which we build up during the recursion as modelling the "call stack" of a more conventionally written function!
Hope that gives part of an answer to your question. If I've gone a little overboard, it's only because I thought that, after recursion itself, continuations are the second really neat, mind-expanding idea in The Little Schemer and programming in general.