Explain the continuation example on p.137 of The Little Schemer

Question

The code in question is this:

(define multirember&co
  (lambda (a lat col)
    (cond
     ((null? lat)
      (col (quote ()) (quote ())))
     ((eq? (car lat) a)
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col newlat
                             (cons (car lat) seen)))))
     (else
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col (cons (car lat) newlat)
                             seen))))))

I've stared at this all day but I can't quite seem to understand it. When you recur on the function you are re-defining col but in the examples they seem to use the original definition. Why wouldn't it change. How can you recur on it without passing in the parameters newlat and seen.

It's hard to explain my question because I seem to just be missing a piece. If perhaps someone could give a more explicit walk-through than the book I may be able to understand how it works.

Unutterable

Your code is missing one closing parentheses. – Holography

Answer 1

Let's step through an example; maybe that will help. :-) For simplicity, I'm just going to use list as the collector/continuation, which will just return a list with the arguments to the continuation.

(multirember&co 'foo '(foo bar) list)

At the start,

a = 'foo
lat = '(foo bar)
col = list

At the first iteration, the (eq? (car lat) a) condition matches, since lat is not empty, and the first element of lat is 'foo. This sets up the next recursion to multirember&co thusly:

a = 'foo
lat = '(bar)
col = (lambda (newlat seen)
        (list newlat (cons 'foo seen))

At the next iteration, the else matches: since lat is not empty, and the first element of lat is 'bar (and not 'foo). Thus, for the next recursion, we then have:

a = 'foo
lat = '()
col = (lambda (newlat seen)
        ((lambda (newlat seen)
           (list newlat (cons 'foo seen)))
         (cons 'bar newlat)
         seen))

For ease of human reading (and avoid confusion), we can rename the parameters (due to lexical scoping), without any change to the program's semantics:

col = (lambda (newlat1 seen1)
        ((lambda (newlat2 seen2)
           (list newlat2 (cons 'foo seen2)))
         (cons 'bar newlat1)
         seen1))

Finally, the (null? lat) clause matches, since lat is now empty. So we call

(col '() '())

which expands to:

((lambda (newlat1 seen1)
   ((lambda (newlat2 seen2)
      (list newlat2 (cons 'foo seen2)))
    (cons 'bar newlat1)
    seen1))
 '() '())

which (when substituting newlat1 = '() and seen1 = '()) becomes

((lambda (newlat2 seen2)
   (list newlat2 (cons 'foo seen2)))
 (cons 'bar '())
 '())

or (evaluating (cons 'bar '()))

((lambda (newlat2 seen2)
   (list newlat2 (cons 'foo seen2)))
 '(bar)
 '())

Now, substituting the values newlat2 = '(bar) and seen2 = '(), we get

(list '(bar) (cons 'foo '()))

or, in other words,

(list '(bar) '(foo))

to give our final result of

'((bar) (foo))

Umbelliferous

First of all, thanks for a thorough and thoughtful explanation. I am still a bit fuzzy on how you get the actual parameters for the inner lambda. How did you know that newlat2 = '(bar) and seen2 = '()? – Unutterable

Let's step you through a simpler example of how argument substitution works. :-) Say you have a function, (define ** (lambda (x y) (exp (* (log x) y)))). If you then call (** 42 24), then that calls the lambda with x = 42 and y = 24. Since ** is the same as the lambda, the equivalent expression is ((lambda (x y) (exp (* (log x) y))) 42 24). Hopefully that makes some sense. :-) – Umbelliferous

Now to directly answer your question of how we get newlat2 = '(bar) and seen2 = '(), it's simply calling that lambda with those given arguments. Consider the expression ((lambda (newlat2 seen2) ...) '(bar) '()). If we gave that lambda a name, say inner, then that expression simply becomes (inner '(bar) '()). It's easy to see, then, why inside the lambda, newlat2 and seen2 would have the values listed. – Umbelliferous

Oh wow, okay I think I see it now. You nailed it with your last explanation. I see now why the lambdas have two parens before them. The first is defining the function and the second is evaluating it and it includes the two arguments at the end. Thanks so much! – Unutterable

Answer 2

I found a wonderful answer here: http://www.michaelharrison.ws/weblog/?p=34

I've been struggling through this too. The key is to understand lexical scoping (for me, à la Javascript) and the inner functions passed to multirember&co on the eq and not eq branches. Understand that, and you'll understand the entire procedure.

Floria

Answer 3

I have struggled myself, to understand what is happening inside the multirember&co, for quite a while. The problem is that the moment I thought I've got it - next task/example proved I have not.

What helped me was putting together a visual representation of what is happening (for me text walkthroughs are tough to grasp, for some reason).

So, I have put together two flow-charts:

One, just showing the relations between different steps of recursion:

---

And another one, reflecting actual values:



Now, whenever I feel like I'm loosing 'the thread of an argument' again, I just refer to this flow-charts and it puts me back on track.

Another thing I've understood after looking at the 'whole picture' via flow-chart, is that a-friend function is simply checks whether seen holds any values or not (though it returns it the other way around i.e. #f when there values in seen and #t when seen is empty, which might be confusing.

P.S.: I did similar flow-charts for evens-only*&co, which appears later in the book.

Judah

these are great diagrams (and apparently I upvoted sometime before Nov 12 '17 :) ); show nicely the pipeline for the two values being built on the way back from the base case. some parens are missing here and there though, and I think you've switched the two diagrams in places: the one you say is "reflecting actual values" shows the variable names; the other one uses the values. Great visualization, overall. – Porfirioporgy

@WillNess, thanks for notifying about images entanglement (fixed). I will take a look at missed parentheses as well, sometime later. – Judah

Missing parenthesis are now fixed (I believe =) – Judah

@WillNess, I appreciate you taking a look (was hesitated explicitly to ask you to do) – Judah

Answer 4

What the link above (http://www.michaelharrison.ws/weblog/?p=34) explains well is how this whole exercise is about avoiding the imperative programming (C, Java) need to declare two "holder" or "collector" variables ( or lists, vectors) explicitly in memory to catch your answers as you iterate through the list. With FP language Scheme's use of continuation, you do not "push" the test results as you step through (strawberries tuna and swordfish) into any separately created "baskets;" instead, you are consing together two lists as you send the appropriate consing functions -- one for eq? true, the other for eq? false -- through the recurs . . . finally ending up at the third col function which, in TLS's first example, is "a-friend" which asks whether the list built to hold all the matches is empty (null?). TLS then asks you to "run" multirember&co again with a new "last" col that merely asks the list containing all the "not tuna" atoms how many it contains ("last-friend"). So there are two "first class" functions being used to work with the task of collecting, i.e. building two separate lists, then at the end of the recursion unwinding, the original col ("a-friend") ask the final question. Maybe the name "multirember&co" is not the greatest name, because it really doesn't rebuild the list minus the atom to be removed; rather, it builds two separate lists -- which never get displayed -- then applies the final col (a-friend or last-friend) . . . which displays either #t or #f, or the length of the "not tuna" list.

Here's some output:

> (multirember&co 'tuna '(and tuna) a-friend)
#f
> (multirember&co 'tuna '(and not) a-friend)
#t

Here's a col to give back a list of non-matches:

(define list-not  (lambda (x y) x))

and its use:

> (multirember&co 'tuna '(and not) list-not)
(and not)

Nagari

Answer 5

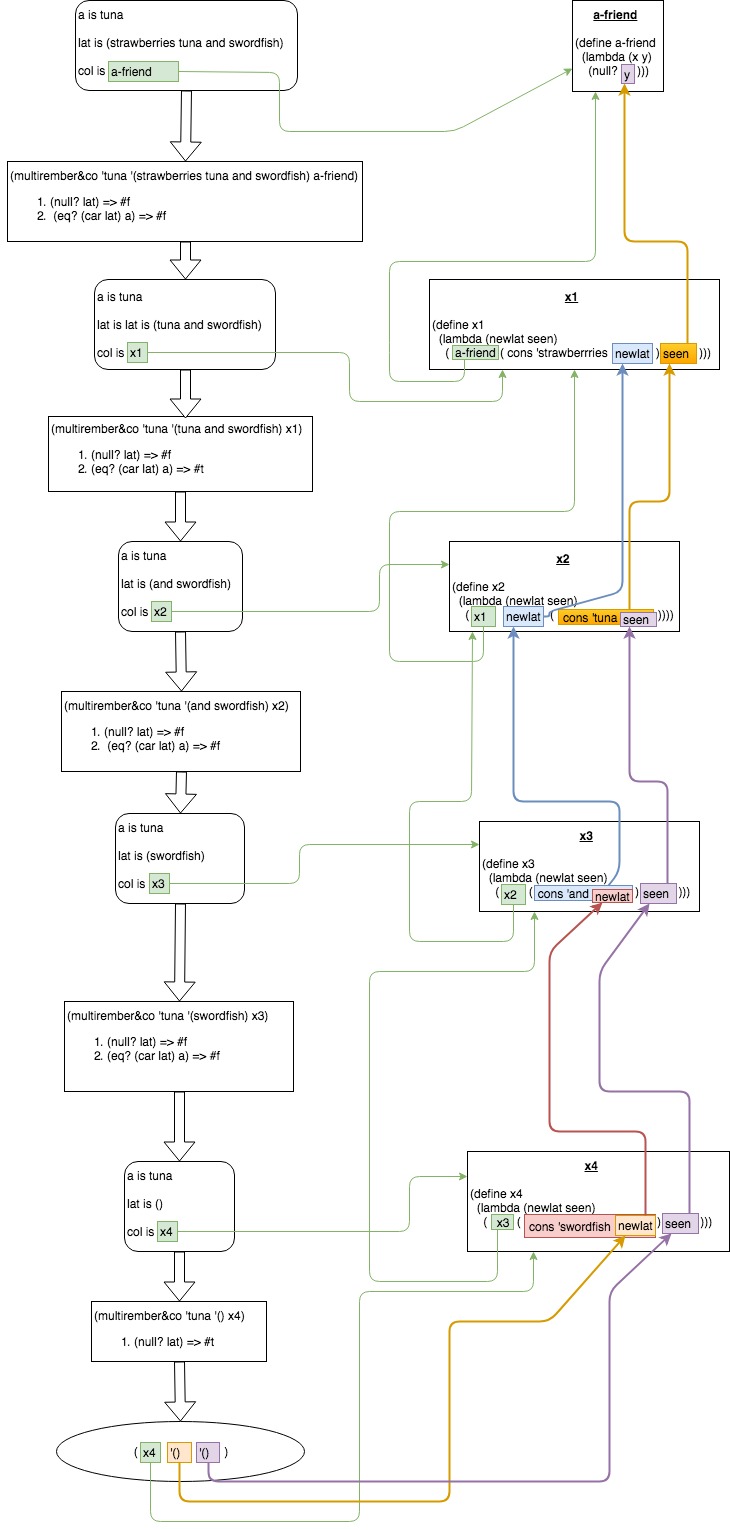
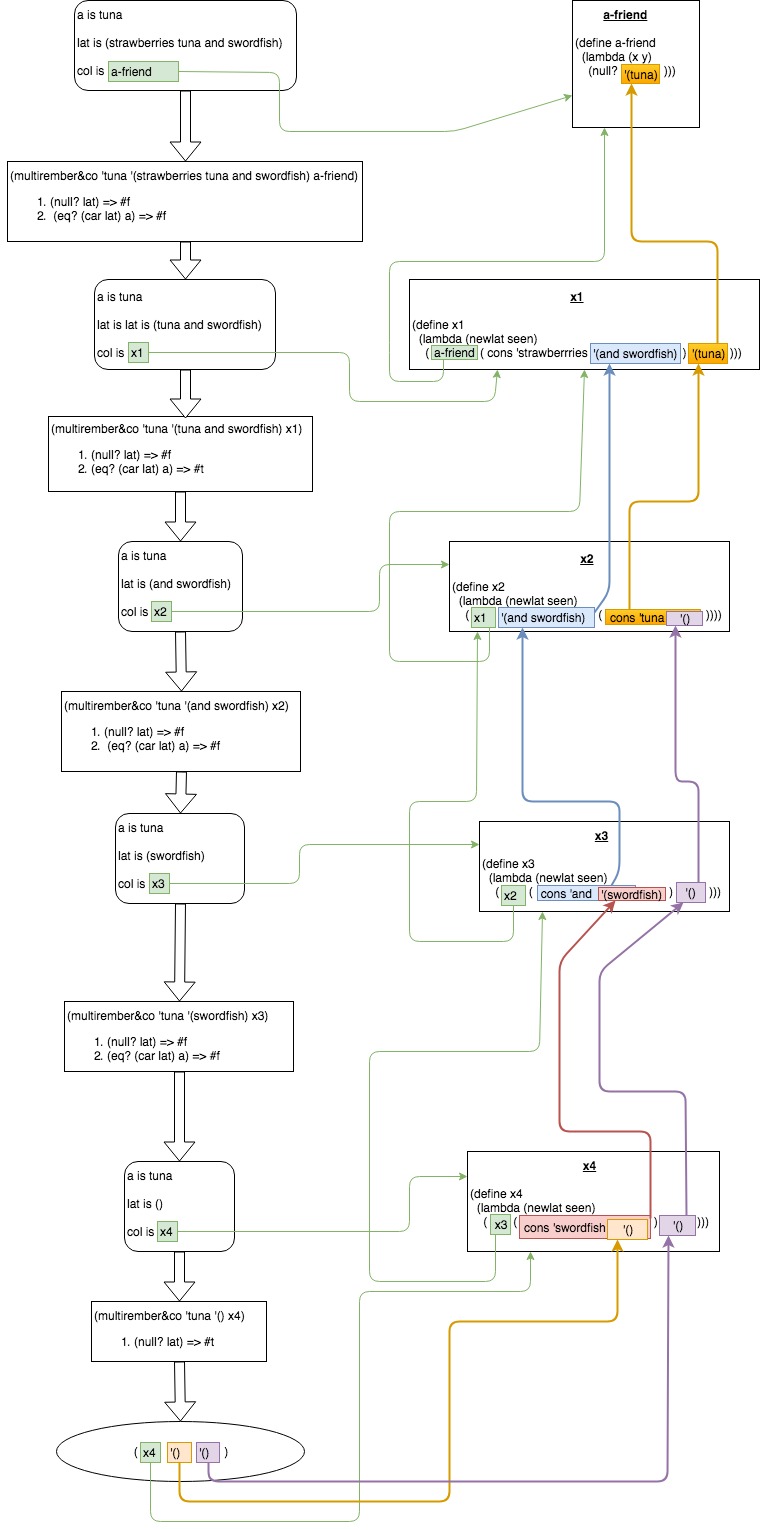
Let's use some equational pseudocode with some parentheses omitted for clarity (so, we write f x y for the call (f x y), where this is unambiguous):

multirember&Co a lat col
    = col [] []                                , IF lat == [] 

    = multirember&Co a (cdr lat)
         ( newlat seen => 
             col newlat
                 (cons (car lat) seen) )       , IF (car lat) == a

    = multirember&Co a (cdr lat)
         ( newlat seen => 
             col (cons (car lat) newlat)
                 seen )                        , OTHERWISE

Isn't it just self-evident, what this does? :) Not yet? :) Re-writing again with an imagined pattern-matching pseudocode (with guards), we have

multirember&Co  =  g   where
    g a [b, ...lat] col | b == a  =  g a lat ( n s =>  col     n     [b, ...s] )
                        | else    =  g a lat ( n s =>  col [b, ...n]     s     )
    g a []          col           =                    col     []        []

The semantics of pattern matching should be quite obvious: [b, ...lat] matches [1,2,3] where b = 1 and lat = [2,3]. This is thus just a three-cased equation:

• When the second argument is an empty list, the "collector" function col is fed two empty lists as its two arguments right away;

• When the second argument's (which is a list) head element is the same as the first argument, the result is the same as that for recursing with the tail of the list, with the amended collector which -- after it will receive its two arguments, n and s, -- will prepend the current head element (which is a) to the s list, and will feed the two lists to this invocation's collector function col;

• Otherwise, the head element will be prepended to the n list, after n and s are received by the constructed collector, and the both will be fed further into the current collector function.

In other words we're dealing with two results coming back from the recursive call, prepending the head to the second if the head was a, or to the first if it wasn't.

Thus the call

    (g 1 [ 2, 1, 3, 1, 4, 5 ] col)

is the same as (will result in) the call

    (col [ 2, ...[3, ...[4, ...[5, ...[]]]]]
         [    1, ...[1,            ...[]]  ])

i.e.

    (col [ 2,     3,     4,     5          ]
         [    1,     1                     ])

---

Another way to look at it is that the following is another, equivalent formulation:

multirember&Co a lat col  =  g a lat id id   where
    id      x  =  x              ; identity function  
    (f ∘ g) x  =  f (g x)        ; function composition
    g a [b, ...lat] c d 
               | b == a  =  g a lat  c     (d ∘ (x => cons b x))  ;    (d ∘ {cons b})
               | else    =  g a lat (c ∘ (x => cons b x))   d     ; (c ∘ {cons b})
    g a []          c d  =  col     (c [])                (d [])

and thus

multirember&Co 1 [ 2, 1, 3, 1, 4, 5 ] col 
=
col (((((id ∘ {cons 2}) ∘ {cons 3}) ∘ {cons 4}) ∘ {cons 5}) [])   ; { } is for
    ( ( (id ∘       {cons 1}) ∘ {cons 1}                  ) [])   ;  partial application
=
col     (id   (cons 2     (cons 3     (cons 4    (cons 5   [])))))
        (id         (cons 1     (cons 1                    []) ) )  

which is self-evidently the same thing.

In yet another pseudocode (with list comprehensions), this reveals itself to be

multirember&Co a lat col  
   = col [ b for b in lat if (b /= a) ] 
         [ b for b in lat if (b == a) ] 
   = ( ((n,s) => col n s) ∘ {partition {/= a}} ) lat

except that only one traversal of the list lat is performed (in the original code), efficiently, building the nested chain of lambda functions mimicking the original list structure; which chain is then evaluated to create the two results, passing them to the top-most collector function col.

All this shows us the power of Continuation-Passing Style (which is what this is) to, in effect, create its own function call protocol, here for example passing back two results from each recursive function call, even though normally in lambda calculus a function can only have one result (even if, say, a pair).

Porfirioporgy

Well, I am flattered, of course, that you asked for my opinion =). To be honest: until the last code snippet (one with list comprehensions) — I thought that while this answer explains/illustrates what happens, well enough, it would be hard for me to evaluate it, as I have grasped the most of what it explains already. Though, your example with list comprehensions 'saved the day' (it made me see this style of coding from yet another angle). So thanks for the time and effort put in this answer! – Judah

I meant visually, does it help to see easily what's going on. For me, the 2nd from the top is the clearest. Even though I know what it does, the original Scheme code is like a wall of words to me. when I'm reading it, I can only see one clause at a time at the most, so I'm forced to remembering the rest. With that pseudocode though, I can see it all at once. YMMV of course. thanks for the feedback! – Porfirioporgy

Answer 6

The code does not build the solution, as it happens usually, but it builds a code that computes the solution, exactly as when you would build the tree using low level operations, like cons, +, -, etc, instead of using high level accumulators or filters.

This is why it is difficult to say if the process is iterative or recursive, because, by the definition of the iterative processes, they use a finite amount of memory for the local state. However, this kind of process uses much memory, but this is allocated in environment, not in local parameters.

First, I duplicate the code here, to be able to see the correspondence without scrolling too much:

(define multirember&co
  (lambda (a lat col)
    (cond
     ((null? lat)
      (col (quote ()) (quote ())))
     ((eq? (car lat) a)
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col newlat
                             (cons (car lat) seen)))))
     (else
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col (cons (car lat) newlat)
                             seen)))))))

Let us try to split the problem to see what really happens.

• Case 1:

---

(multirember&co 'a
                '()
                (lambda (x y) (list x y)))

is the same as    

(let ((col (lambda (x y) (list x y))))
  (col '() '()))

This is a trivial case, it never loops.

Now the interesting cases:

• Case 2:

---

(multirember&co 'a
                '(x)
                (lambda (x y) (list x y)))

is the same as    

(let ((col
       (let ((col (lambda (x y) (list x y)))
             (lat '(x))
             (a 'a))
         (lambda (newlat seen)
           (col (cons (car lat) newlat)
                seen)))))
  (col '() '()))

In this case, the process produces this code as result, and finally evaluates it. Note that locally it is still tail-recursive, but globally it is a recursive process, and it requires memory not by allocating some data structure, but by having the evaluator allocate only environment frames. Each loop deepens the environment by adding 1 new frame.

• Case 3

---

(multirember&co 'a
                '(a)
                (lambda (x y) (list x y)))

is the same as    

(let ((col
       (let ((col (lambda (x y) (list x y)))
             (lat '(a))
             (a 'a))
         (lambda (newlat seen)
           (col newlat
                (cons (car lat) seen))))))
  (col '() '()))

This builds the code , but on the other branch, that accumulates a result in the other variable.

---

All the other cases are combinations of 1 of these 3 cases, and it is clear how each 1 acts, by adding a new layer.

Cid

Answer 7

I hope this walkthrough helps

As Chris suggested, I've renamed newlat/seen to n/s and added an index. The book gives horrible names to the functions (a-friend new-friend latest-fried), so I just kept L (for lambda) and the definition.

multirember&co 'tuna '(strawberries tuna and swordfish) a-friend)
  multirember&co 'tuna '(tuna and swordfish) (L(n1 s1)(a-friend (cons 'strawberries n1) s1))
    multirember&co 'tuna '(and swordfish) (L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))
      multirember&co 'tuna '(swordfish) (L(n3 s3)((L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2)) (cons 'and n3) s3))
        multirember&co 'tuna '() (L(n4 s4)((L(n3 s3)((L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2)) (cons 'and n3) s3)) (cons 'swordfish n4) s4))

((lambda(n4 s4)((lambda(n3 s3)((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) (cons 'and n3) s3)) (cons 'swordfish n4) s4)) '() '())
               ((lambda(n3 s3)((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) (cons 'and n3) s3)) '(swordfish) '())
                              ((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) '(and swordfish) '())
                                             ((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) '(and swordfish) '(tuna))
                                                            (a-friend '(strawberries and swordfish) '(tuna))

Ingrate