Generate random numbers according to distributions

Question

I want to generate random numbers according some distributions. How can I do this?

Tourist

Putting aside the fact that computers only generate pseudo-random numbers, surely if they are generated to a known distribution then they aren't random at all. Which distributions are you looking to generate sample data for? – Emarie

Easiest way is to find a library that does this. Do you have any particular language in mind? – Cacology

If you use Java, you can try the Uncommons Maths library by Dan Dyer (notice the previous comment) which provides random number generators, probability distributions, combinatorics and statistics. – Pyrophyllite

Answer 1

The standard random number generator you've got (rand() in C after a simple transformation, equivalents in many languages) is a fairly good approximation to a uniform distribution over the range [0,1]. If that's what you need, you're done. It's also trivial to convert that to a random number generated over a somewhat larger integer range.

Conversion of a Uniform distribution to a Normal distribution has already been covered on SO, as has going to the Exponential distribution.

[EDIT]: For the triangular distribution, converting a uniform variable is relatively simple (in something C-like):

double triangular(double a,double b,double c) {
   double U = rand() / (double) RAND_MAX;
   double F = (c - a) / (b - a);
   if (U <= F)
      return a + sqrt(U * (b - a) * (c - a));
   else
      return b - sqrt((1 - U) * (b - a) * (b - c));
}

That's just converting the formula given on the Wikipedia page. If you want others, that's the place to start looking; in general, you use the uniform variable to pick a point on the vertical axis of the cumulative density function of the distribution you want (assuming it's continuous), and invert the CDF to get the random value with the desired distribution.

Brainpan

no i just need to have some numbers that are in exponential,normal,triangular...etc? Rockwell Arena input analyser does this but i dont know how to use it? – Tourist

+1 I appreciate this C pseudocode, because I was looking at wikipedia's article on triangular distribution, and couldn't figure out how to turn it into code. One correction: rand() returns an integer from 0 to RAND_MAX, so I think you want U = ((double)rand()) / RAND_MAX. Otherwise, your sqrt((1 - U) ...) is going to come out imaginary. – Pietrek

@LarsH: Damn! Forgot that C is odd that way. Thanks for the correction. – Brainpan

Answer 2

The right way to do this is to decompose the distribution into n-1 binary distributions. That is if you have a distribution like this:

A: 0.05
B: 0.10
C: 0.10
D: 0.20
E: 0.55

You transform it into 4 binary distributions:

1. A/E: 0.20/0.80
2. B/E: 0.40/0.60
3. C/E: 0.40/0.60
4. D/E: 0.80/0.20

Select uniformly from the n-1 distributions, and then select the first or second symbol based on the probability if each in the binary distribution.

Code for this is here

Malda

You're presuming the distribution is discrete. – Manzano

I sure am - which is the typical case in programming ( e.g. probability transition tables, hidden markov models etc. ). But if you notice the method is constant time. This means there is no time performance penalty for generting huge distributions. So for a continuous distribution, you could discritize it into as many bins as you need to get a good enough approximation and use my method. – Malda

Discrete RVs may be most common in the kind of programming you do, but lots of us need Gaussian, exponential, triangular, log-normal, beta, gamma, Weibull, etc, etc distributions for our work. Even with discrete distributions they don't work for infinite ranges (Poisson, geometric). Alias tables generate values in constant time but so do most continuous inversions or compositions. Meanwhile, approximating continuous distributions with tables takes massive setup and storage not needed by computational approaches. Alias tables are lovely when applicable, but they're not a general solution. – Manzano

A very clever method to generate nonuniform random numbers in constant time if the distribution cannot be expressed by a function or you do not know how to express it. If you have a distribution table as fine-grain as possible, it can well approximate the distribution. Thank you for providing this piece of information. – Ahmednagar

Answer 3

It actually depends on distribution. The most general way is the following. Let P(X) be the probability that random number generated according to your distribution is less than X.

You start with generating uniform random X between zero and one. After that you find Y such that P(Y) = X and output Y. You could find such Y using binary search (since P(X) is an increasing function of X).

This is not very efficient, but works for distributions where P(X) could be efficiently computed.

Favorite

Answer 4

You can look up inverse transform sampling, rejection sampling as well as the book by Devroye "Nonuniform random variate generation"/Springer Verlag 1986

Delouse

Answer 5

In the past few years, nice new tools have been added to SciPy to address this kind of problem in Python. You can easily generate samples from custom continuous or discrete univariate distributions by just providing some information about the distribution, such as the density / pdf.

Overview of the different methods: https://docs.scipy.org/doc/scipy/reference/stats.sampling.html

Tutorial: https://docs.scipy.org/doc/scipy/tutorial/stats/sampling.html

If you are using R, very similar functionality is available in Runuran (https://CRAN.R-project.org/package=Runuran).

C library UNURAN: https://statmath.wu.ac.at/unuran/doc.html

Here is an example in Python:

import numpy as np
from scipy.stats.sampling import NumericalInversePolynomial
from matplotlib import pyplot as plt
from scipy.integrate import quad


class MyDist:
    def __init__(self, a):
        self.a = a

    def support(self):
        # distribution restricted to 0, 5, can be changed as needed
        return (0, 5)

    def pdf(self, x):
        # this is not a proper pdf, the normalizing
        # constant is missing (does not integrate to one)
        return x * (x + np.sin(5*x) + 2) * np.exp(-x**self.a)


dist = MyDist(0.5)
gen = NumericalInversePolynomial(dist)

# compute the missing normalizing constant to plot the pdf
const_pdf = quad(dist.pdf, *dist.support())[0]

r = gen.rvs(size=50000)
x = np.linspace(r.min(), r.max(), 500)

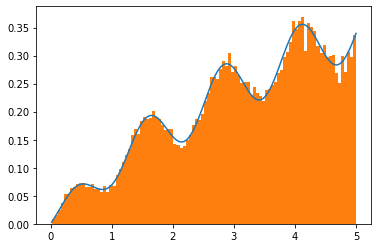
# show histogram together with the pdf
plt.plot(x, dist.pdf(x) / const_pdf)
plt.hist(r, density=True, bins=100)
plt.show()

Monocyclic

Answer 6

You can convert from discrete bins to float/double with interpolation. Simple linear works well. If your table memory is constrained other interpolation methods can be used. -jlp

Aleishaalejandra

Answer 7

It's a standard textbook matter. See here for some code, or here at Section 3.2 for some reference mathematical background (actually very quick and simple to read).

Jordison