Converting a Uniform Distribution to a Normal Distribution

Question

How can I convert a uniform distribution (as most random number generators produce, e.g. between 0.0 and 1.0) into a normal distribution? What if I want a mean and standard deviation of my choosing?

Yourself

Do you have a language specification, or is this just a general algorithm question? – Pangermanism

General algorithm question. I don't care which language. But I would prefer that the answer not rely on specific functionality that only that language provides. – Yourself

Answer 1

There are plenty of methods:

• Do not use Box Muller. Especially if you draw many gaussian numbers. Box Muller yields a result which is clamped between -6 and 6 (assuming double precision. Things worsen with floats.). And it is really less efficient than other available methods.
• Ziggurat is fine, but needs a table lookup (and some platform-specific tweaking due to cache size issues)
• Ratio-of-uniforms is my favorite, only a few addition/multiplications and a log 1/50th of the time (eg. look there).
• Inverting the CDF is efficient (and overlooked, why ?), you have fast implementations of it available if you search google. It is mandatory for Quasi-Random numbers.

Feaster

Are you sure about the [-6,6] clamping? This a pretty significant point if true (and worthy of a note on the wikipedia page). – Loosejointed

@locster: this is what a teacher of mine told me (he studied such generators, and I trust his word). I may be able to find you a reference. – Feaster

@locster: this undesirable property is also shared by the inverse CDF method. See cimat.mx/~src/prope08/randomgauss.pdf . This can be alleviated by using a uniform RNG which has non zero probability to yield a floating point number very close to zero. Most RNG do not, since they generate a (typically 64 bit) integer which is then mapped to [0,1]. This makes those methods unsuitable for sampling tails of gaussian variables (think of pricing low/high strike options in computational finance). – Feaster

Indeed, consider x1 = 1/(2^32-1) (smallest random number greater than zero, generated with 32-bit integer) and x2 = 0. Then random = sqrt(-2 ln(1/(2^32-1))) * cos(2 * pi * 0) = 6.6604. With 64-bit random number generator this is about 9.419. – Saucepan

@AlexandreC. Just to be clear on two points, using 64-bit numbers the tails go out to either 8.57 or 9.41 (the lower value corresponding to converting to [0,1) before taking the log). Even if clamped to [-6, 6] the chances of being outside this range are about 1.98e-9, good enough for most people even in science. For the 8.57 and 9.41 figures this becomes 1.04e-17 and 4.97e-21. These numbers are so small that the difference between a Box Muller sampling and a true gaussian sampling in terms of said limit are almost purely academic. If you need better, just add up four of them and divide by 2. – Brenn

I know this was a long time ago, but @AlexandreC. could you please provide a link to that document about the clamping effect when using the inverse CDF method? The link on the comment above is dead now. Thank you. – Makeup

I think the suggestion to not use the Box Muller transform is misleading for a large percentage of users. It is great to know about the limitation, but as CrazyCasta points out, for most applications that aren't heavily dependent on outliers, you probably don't need to worry about this. As an example, if you have ever depended on sampling from a normal using numpy, you have depended on the Box Muller transform (polar coordinate form) github.com/numpy/numpy/blob/… . – Elaterium

This answer appears to miss a criticial point: if you use a single discrete random variable (such as a 32 bits floating-point value), any transform will also be discrete with at best the same number of values. (At best, because f(x)=f(y) does not imply x=y but the reverse is true). Box Muller does not produce results above 6, sure, but every transform has a finite limit. – Charr

@Charr Sure, this is going to happen regardless of the method (at least if you don't use rejection). Ratio-of-uniforms or ziggurat have better properties for extreme values though. 9 years later of XP with normal distributions, I'd still recommend one of those over Box-Muller, especially for 1) performance reasons, 2) better use of rejection. If you use quasi-random sequence (Sobol, etc) you have no choice but using the inverse-cdf though. – Feaster

The cimat.mx/~src/prope08/randomgauss.pdf URL is AWOL (404), with either http or https protocol. The WayBack Machine (web.archive.org) tried to scan it on 2013-05-28 and failed to find it then. The document is essentially lost. – Elysia

On your first point, the algorithm that sums 12 uniform(0,1) random numbers and subtracts by 6 is not the "Box Muller" algorithm, but an approximation of the normal distribution. On the other hand, the Box Muller method is "exact" assuming we can generate and store any real number. – Polity

@PeterO. I didn't say that. Box-Muller has clamping problems coming from the nature of floating point arithmetic. Many algorithms have the same problem. – Feaster

Answer 2

The Ziggurat algorithm is pretty efficient for this, although the Box-Muller transform is easier to implement from scratch (and not crazy slow).

Tolan

The usual warnings about linear congruent generators apply to both these methods, so use a decent underling generator. Cheers. – Mahaffey

Such as Mersenee Twister, or do you have other suggestions? – Chem

Answer 3

Changing the distribution of any function to another involves using the inverse of the function you want.

In other words, if you aim for a specific probability function p(x) you get the distribution by integrating over it -> d(x) = integral(p(x)) and use its inverse: Inv(d(x)). Now use the random probability function (which have uniform distribution) and cast the result value through the function Inv(d(x)). You should get random values cast with distribution according to the function you chose.

This is the generic math approach - by using it you can now choose any probability or distribution function you have as long as it have inverse or good inverse approximation.

Hope this helped and thanks for the small remark about using the distribution and not the probability itself.

Visional

+1 This is an overlooked method for generating gaussian variables which works very well. Inverse CDF can be efficiently computed with Newton method in this case (derivative is e^{-t^2}), an initial approximation is easy to get as a rational fraction, so you need 3-4 evaluations of erf and exp. It is mandatory if you use quasi-random numbers, a case where you must use exactly one uniform number to get a gaussian one. – Feaster

Note that you need to invert the cumulative distribution function, not the probability distribution function. Alexandre implies this, but I thought mentioning it more explicitly might not hurt - since the answer seems to suggest the PDF – Septum

You can use the PDF if you're prepared to randomly select a direction relative to the mean; do I understand that right? – Chrystal

This is called Inverse transform sampling – Knock

Here is related question in SE with a more generalized answer with nice explanation. – Knock

Answer 4

Here is a javascript implementation using the polar form of the Box-Muller transformation.

/*
 * Returns member of set with a given mean and standard deviation
 * mean: mean
 * standard deviation: std_dev 
 */
function createMemberInNormalDistribution(mean,std_dev){
    return mean + (gaussRandom()*std_dev);
}

/*
 * Returns random number in normal distribution centering on 0.
 * ~95% of numbers returned should fall between -2 and 2
 * ie within two standard deviations
 */
function gaussRandom() {
    var u = 2*Math.random()-1;
    var v = 2*Math.random()-1;
    var r = u*u + v*v;
    /*if outside interval [0,1] start over*/
    if(r == 0 || r >= 1) return gaussRandom();

    var c = Math.sqrt(-2*Math.log(r)/r);
    return u*c;
    
    /* todo: optimize this algorithm by caching (v*c) 
     * and returning next time gaussRandom() is called.
     * left out for simplicity */
}

Quicktempered

The interval you have there for your r variable is actually (0,1], not [0,1], because when r equals zero, you start over. – Urinary

Algorithm seems to generate only non-negative numbers. You need a random sign flip to fix this. – Possible

Answer 5

Use the central limit theorem wikipedia entry mathworld entry to your advantage.

Generate n of the uniformly distributed numbers, sum them, subtract n*0.5 and you have the output of an approximately normal distribution with mean equal to 0 and variance equal to (1/12) * (1/sqrt(N)) (see wikipedia on uniform distributions for that last one)

n=10 gives you something half decent fast. If you want something more than half decent go for tylers solution (as noted in the wikipedia entry on normal distributions)

Batsman

This won't give a particularly close normal (the "tails" or end-points will not be close to the real normal distribution). Box-Muller is better, as others have suggested. – Brokendown

Box Muller has wrong tails too (it returns a number between -6 and 6 in double precision) – Feaster

n=12 (sum 12 random numbers in the range 0 to 1, and subtract 6) results in stddev=1 and mean=0. This can then be used to generation any normal distribution. Simply multiply the result by the desired stddev and add the mean. – Ahrendt

Tails beyond 6 are probably not going to occur in your model, unless you are using billions of random numbers. And if you are using billions, you are probably doing your monte carlo model wrong. – Possible

Answer 6

Where R1, R2 are random uniform numbers:

NORMAL DISTRIBUTION, with SD of 1:

sqrt(-2*log(R1))*cos(2*pi*R2)

This is exact... no need to do all those slow loops!

Reference: dspguide.com/ch2/6.htm

Blearyeyed

Before someone corrected me... here's the approximation I came up with: (1.5-(R1+R2+R3))*1.88. I like it too. – Blearyeyed

thanks, also found this equation here dspguide.com/ch2/6.htm – Eliathan

This is the Box-Muller transform mentioned in a number of other answers, with the same limitations discussed there. Note that you can get a second normal random deviate from R1 and R2 by also calculating the sine. More details on Box-Muller here. – Sprite

Answer 7

I would use Box-Muller. Two things about this:

1. You end up with two values per iteration
   Typically, you cache one value and return the other. On the next call for a sample, you return the cached value.
2. Box-Muller gives a Z-score
   You have to then scale the Z-score by the standard deviation and add the mean to get the full value in the normal distribution.

Pentobarbital

How do you scale the Z-score? – Yourself

scaled = mean + stdDev * zScore // gives you normal(mean,stdDev^2) – Counterpunch

Answer 8

It seems incredible that I could add something to this after eight years, but for the case of Java I would like to point readers to the Random.nextGaussian() method, which generates a Gaussian distribution with mean 0.0 and standard deviation 1.0 for you.

A simple addition and/or multiplication will change the mean and standard deviation to your needs.

Adila

This is Marsaglia's disc method. – Possible

Answer 9

The standard Python library module random has what you want:

normalvariate(mu, sigma)
Normal distribution. mu is the mean, and sigma is the standard deviation.

For the algorithm itself, take a look at the function in random.py in the Python library.

The manual entry is here

Festinate

Unfortunately, python's library uses Kinderman,A.J. and Monahan, J.F., "Computer generation of random variables using the ratio of uniform deviates", ACM Trans Math Software, 3, (1977), pp257-260. This uses two uniform random variables to generate the normal value, rather than a single one, so it isn't obvious how to use it as the mapping that the OP wanted. – Feuar

Answer 10

This is my JavaScript implementation of Algorithm P (Polar method for normal deviates) from Section 3.4.1 of Donald Knuth's book The Art of Computer Programming:

function normal_random(mean,stddev)
{
    var V1
    var V2
    var S
    do{
        var U1 = Math.random() // return uniform distributed in [0,1[
        var U2 = Math.random()
        V1 = 2*U1-1
        V2 = 2*U2-1
        S = V1*V1+V2*V2
    }while(S >= 1)
    if(S===0) return 0
    return mean+stddev*(V1*Math.sqrt(-2*Math.log(S)/S))
}

Sou

Answer 11

I thing you should try this in EXCEL: =norminv(rand();0;1). This will product the random numbers which should be normally distributed with the zero mean and unite variance. "0" can be supplied with any value, so that the numbers will be of desired mean, and by changing "1", you will get the variance equal to the square of your input.

For example: =norminv(rand();50;3) will yield to the normally distributed numbers with MEAN = 50 VARIANCE = 9.

Dairen

Answer 12

Q How can I convert a uniform distribution (as most random number generators produce, e.g. between 0.0 and 1.0) into a normal distribution?

1. For software implementation I know couple random generator names which give you a pseudo uniform random sequence in [0,1] (Mersenne Twister, Linear Congruate Generator). Let's call it U(x)

2. It is exist mathematical area which called probibility theory. First thing: If you want to model r.v. with integral distribution F then you can try just to evaluate F^-1(U(x)). In pr.theory it was proved that such r.v. will have integral distribution F.

3. Step 2 can be appliable to generate r.v.~F without usage of any counting methods when F^-1 can be derived analytically without problems. (e.g. exp.distribution)

4. To model normal distribution you can cacculate y1*cos(y2), where y1~is uniform in[0,2pi]. and y2 is the relei distribution.

Q: What if I want a mean and standard deviation of my choosing?

You can calculate sigma*N(0,1)+m.

It can be shown that such shifting and scaling lead to N(m,sigma)

Keos

Answer 13

This is a Matlab implementation using the polar form of the Box-Muller transformation:

Function randn_box_muller.m:

function [values] = randn_box_muller(n, mean, std_dev)
    if nargin == 1
       mean = 0;
       std_dev = 1;
    end

    r = gaussRandomN(n);
    values = r.*std_dev - mean;
end

function [values] = gaussRandomN(n)
    [u, v, r] = gaussRandomNValid(n);

    c = sqrt(-2*log(r)./r);
    values = u.*c;
end

function [u, v, r] = gaussRandomNValid(n)
    r = zeros(n, 1);
    u = zeros(n, 1);
    v = zeros(n, 1);

    filter = r==0 | r>=1;

    % if outside interval [0,1] start over
    while n ~= 0
        u(filter) = 2*rand(n, 1)-1;
        v(filter) = 2*rand(n, 1)-1;
        r(filter) = u(filter).*u(filter) + v(filter).*v(filter);

        filter = r==0 | r>=1;
        n = size(r(filter),1);
    end
end

And invoking histfit(randn_box_muller(10000000),100); this is the result:

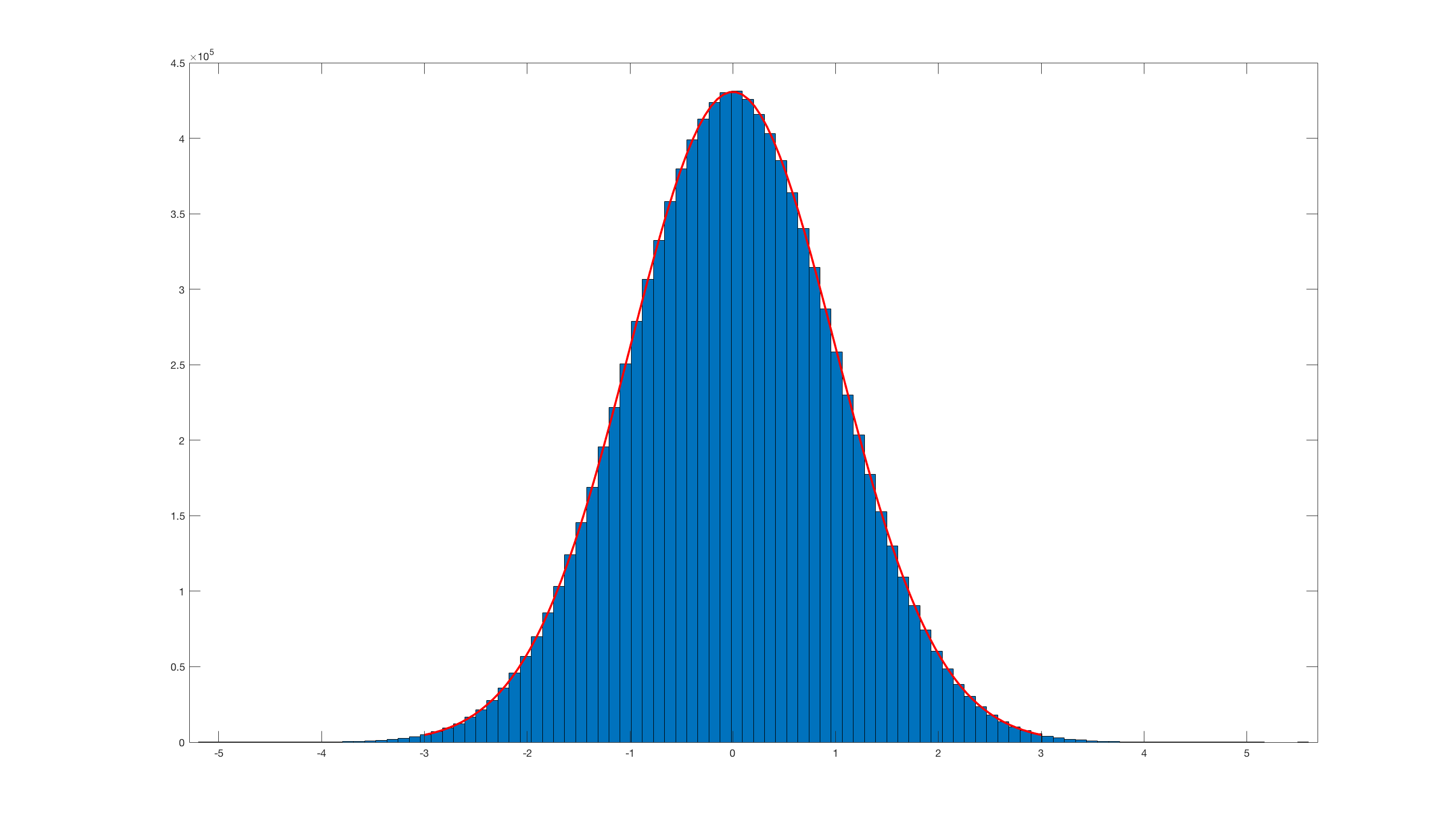
Obviously it is really inefficient compared with the Matlab built-in randn.

Mindi

Answer 14

I have the following code which maybe could help:

set.seed(123)
n <- 1000
u <- runif(n) #creates U
x <- -log(u)
y <- runif(n, max=u*sqrt((2*exp(1))/pi)) #create Y
z <- ifelse (y < dnorm(x)/2, -x, NA)
z <- ifelse ((y > dnorm(x)/2) & (y < dnorm(x)), x, z)
z <- z[!is.na(z)]

Laminous

Answer 15

It is also easier to use the implemented function rnorm() since it is faster than writing a random number generator for the normal distribution. See the following code as prove

n <- length(z)
t0 <- Sys.time()
z <- rnorm(n)
t1 <- Sys.time()
t1-t0

Peaceable

Answer 16

My computer, a WP-34s, is very old, slow, and has limited memory. The following two-instruction sequence works well to generate a normal deviate from a distribution of mean 0 and variance 1, and lifts the stack only one level, but is incredibly slow:

RAND#

Phi-1

I suspect that the reason it is slow is that Phi-1 is actually solving Phi by an iterative process, as mentioned in a previous answer. Possibly this was because the machine designers were running out of memory.

One of the great mysteries of this simplicity is that its execution time is very irregular, possibly depending on the value generated by the RAND# function. But it is very memory frugal, requiring no pre-stored constants or use of other registers.

For greater speed, at the expense of another 16 program memory steps,

RAND# RAND#

RAND# RAND# c-

RAND# RAND# c+

RAND# RAND# c-

RAND# RAND# c+

RAND# RAND# c- +

Note the use of complex addition and subtraction to save a few steps. Also,by alternating addition and subtraction, there is no need to subtract a constant at the end. The mean will be zero, and with 12 uniform randoms, the variance will be 1. No memory other than the four level stack is required. It is hundreds of times faster than the above probability inverse transform method, but it fails at the tails like Box-Muller has been reported to do.

If there is plenty of program memory, I would suggest a rational function approximation to the central part of the inverse CDF, and a recursive solution for the outer 1% tails. Do the slow thing only 1% of the time.

*** Note: the WP-34s is no longer commonly available, but you can download a free emulator for both iPhone and Windows. The iPhone emulator is typically 100 times faster than the original machine that was flashed into a repurposed HP-30 Business Analyst calculator.

Possible

Answer 17

function distRandom(){
  do{
    x=random(DISTRIBUTION_DOMAIN);
  }while(random(DISTRIBUTION_RANGE)>=distributionFunction(x));
  return x;
}

Anaclinal

Not guaranteed to return, though, is it? ;-) – Brokendown

Random numbers are too important to be left to chance. – Treadmill

Doesn't answer the question -- the normal distribution has an infinite domain. – Kosiur