How to interpret the values returned by numpy.correlate and numpy.corrcoef?

Question

I have two 1D arrays and I want to see their inter-relationships. What procedure should I use in numpy? I am using numpy.corrcoef(arrayA, arrayB) and numpy.correlate(arrayA, arrayB) and both are giving some results that I am not able to comprehend or understand.

Can somebody please shed light on how to understand and interpret those numerical results (preferably, using an example)?

Heresiarch

Answer 1

numpy.correlate simply returns the cross-correlation of two vectors.

if you need to understand cross-correlation, then start with http://en.wikipedia.org/wiki/Cross-correlation.

A good example might be seen by looking at the autocorrelation function (a vector cross-correlated with itself):

import numpy as np

# create a vector
vector = np.random.normal(0,1,size=1000) 

# insert a signal into vector
vector[::50]+=10

# perform cross-correlation for all data points
output = np.correlate(vector,vector,mode='full')

This will return a comb/shah function with a maximum when both data sets are overlapping. As this is an autocorrelation there will be no "lag" between the two input signals. The maximum of the correlation is therefore vector.size-1.

if you only want the value of the correlation for overlapping data, you can use mode='valid'.

Diplegia

it's an old, but because I have the same question, I can't understand how I come to the conclusion. Do I have or don't I have autocorrelation on the report? How do I translate the output ? – Whorton

Answer 2

I can only comment on numpy.correlate at the moment. It's a powerful tool. I have used it for two purposes. The first is to find a pattern inside another pattern:

import numpy as np
import matplotlib.pyplot as plt

some_data = np.random.uniform(0,1,size=100)
subset = some_data[42:50]

mean = np.mean(some_data)
some_data_normalised = some_data - mean
subset_normalised = subset - mean

correlated = np.correlate(some_data_normalised, subset_normalised)
max_index = np.argmax(correlated)  # 42 !

The second use I have used it for (and how to interpret the result) is for frequency detection:

hz_a = np.cos(np.linspace(0,np.pi*6,100))
hz_b = np.cos(np.linspace(0,np.pi*4,100))

f, axarr = plt.subplots(2, sharex=True)

axarr[0].plot(hz_a)
axarr[0].plot(hz_b)
axarr[0].grid(True)

hz_a_autocorrelation = np.correlate(hz_a,hz_a,'same')[round(len(hz_a)/2):]
hz_b_autocorrelation = np.correlate(hz_b,hz_b,'same')[round(len(hz_b)/2):]

axarr[1].plot(hz_a_autocorrelation)
axarr[1].plot(hz_b_autocorrelation)
axarr[1].grid(True)

plt.show()

Find the index of the second peaks. From this you can work back to find the frequency.

first_min_index = np.argmin(hz_a_autocorrelation)
second_max_index = np.argmax(hz_a_autocorrelation[first_min_index:])
frequency = 1/second_max_index

Orson

This was really helpful. can I ask, why do you take the mean? It looks like shifting the data but correlation is the curve not value, no? – Boastful

@Boastful good question. There will be a good answer to it which I can't tell you other than it doesn't work if you don't subtract the mean of the original signal. – Orson

@Boastful The following answer explains why you subtract the mean, but this person chose to subtract the root mean square (RMS) which achieves essentially the same result to my eye: https://mcmap.net/q/409928/-numpy-correlate-is-not-providing-an-offset – Fistulous

Answer 3

After reading all textbook definitions and formulas it may be useful to beginners to just see how one can be derived from the other. First focus on the simple case of just pairwise correlation between two vectors.

import numpy as np

arrayA = [ .1, .2, .4 ]
arrayB = [ .3, .1, .3 ]

np.corrcoef( arrayA, arrayB )[0,1] #see Homework bellow why we are using just one cell
>>> 0.18898223650461365

def my_corrcoef( x, y ):    
    mean_x = np.mean( x )
    mean_y = np.mean( y )
    std_x  = np.std ( x )
    std_y  = np.std ( y )
    n      = len    ( x )
    return np.correlate( x - mean_x, y - mean_y, mode = 'valid' )[0] / n / ( std_x * std_y )

my_corrcoef( arrayA, arrayB )
>>> 0.1889822365046136

Homework:

• Extend example to more than two vectors, this is why corrcoef returns a matrix.
• See what np.correlate does with modes different than 'valid'
• See what scipy.stats.pearsonr does over (arrayA, arrayB)

One more hint: notice that np.correlate in 'valid' mode over this input is just a dot product (compare with last line of my_corrcoef above):

def my_corrcoef1( x, y ):    
    mean_x = np.mean( x )
    mean_y = np.mean( y )
    std_x  = np.std ( x )
    std_y  = np.std ( y )
    n      = len    ( x )
    return (( x - mean_x ) * ( y - mean_y )).sum() / n / ( std_x * std_y )

my_corrcoef1( arrayA, arrayB )
>>> 0.1889822365046136

Adermin

This should be the correct answer as it addresses the connection between the two functions. – Meingolda

Discussion of np.correlate and normalization is missing? – Eshelman

Answer 4

If you are perplexed by the outcome in case of int vectors, it may be due to overflow:

>>> a = np.array([4,3,2,0,0,10000,0,0], dtype='int16')
>>> np.correlate(a,a[:3], mode='valid')
array([    29,     18,      8,  20000,  30000, -25536], dtype=int16)

How comes?

29 = 4*4 + 3*3 + 2*2
18 = 4*3 + 3*2 + 2*0
 8 = 4*2 + 3*0 + 2*0
...
40000 = 4*10000 + 3*0 + 2*0 shows up as 40000 - 2**16 = -25536

Vevine

Answer 5

Disclaimer: This will not give an answer to How to interpret, but what the difference is between the two:

The difference between them

The Pearson product-moment correlation coefficient (np.corrcoef) is simply a normalized version of a cross-correlation (np.correlate) (source)

So the np.corrcoef is always in a range of -1..+1 and therefore we can better compare different data.

Let me give an example

import numpy as np
import matplotlib.pyplot as plt

# 1. We make y1 and add noise to it
x = np.arange(0,100)
y1 = np.arange(0,100) + np.random.normal(0, 10.0, 100)

# 2. y2 is exactly y1, but 5 times bigger
y2 = y1 * 5

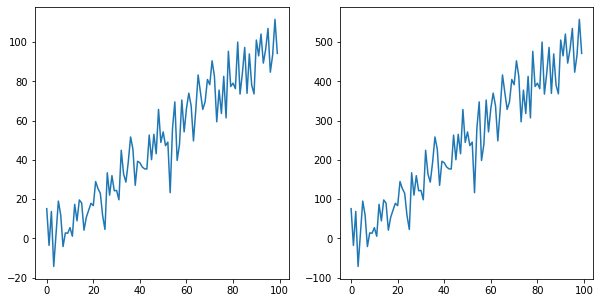
# 3. By looking at the plot we clearly see that the two lines have the same shape
fig, axs = plt.subplots(1,2, figsize=(10,5))
axs[0].plot(x,y1)
axs[1].plot(x,y2)
fig.show()

# 4. cross-correlation can be misleading, because it is not normalized
print(f"cross-correlation y1: {np.correlate(x, y1)[0]}")
print(f"cross-correlation y2: {np.correlate(x, y2)[0]}")
>>> cross-correlation y1 332291.096
>>> cross-correlation y2 1661455.482

# 5. however, the coefs show that the lines have equal correlations with x
print(f"pearson correlation coef y1: {np.corrcoef(x, y1)[0,1]}")
print(f"pearson correlation coef y2: {np.corrcoef(x, y2)[0,1]}")
>>> pearson correlation coef y1 0.950490
>>> pearson correlation coef y2 0.950490

Rooster