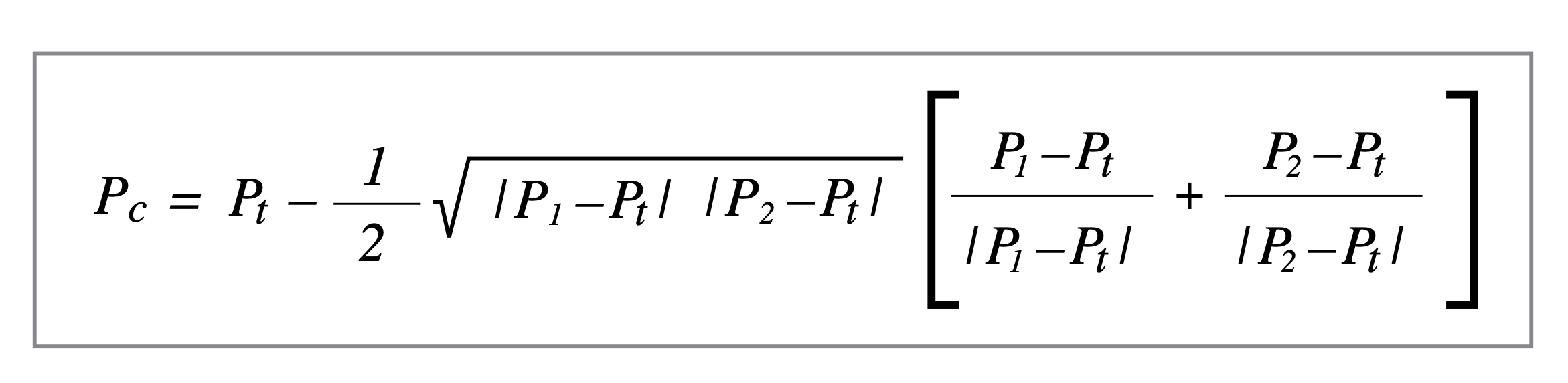Draw a quadratic Bézier curve through three given points

Question

I have three points in 2D and I want to draw a quadratic Bézier curve passing through them. How do I calculate the middle control point (x1 and y1 as in quadTo)? I know linear algebra from college but need some simple help on this.

How can I calculate the middle control point so that the curve passes through it as well?

Milieu

Answer 1

Let P0, P1, P2 be the control points, and Pc be your fixed point you want the curve to pass through.

Then the Bezier curve is defined by

P(t) = P0*t^2 + P1*2*t*(1-t) + P2*(1-t)^2

...where t goes from zero to 1.

There are an infinite number of answers to your question, since it might pass through your point for any value of t... So just pick one, like t=0.5, and solve for P1:

Pc = P0*.25 + P1*2*.25 + P2*.25

P1 = (Pc - P0*.25 - P2*.25)/.5

   = 2*Pc - P0/2 - P2/2

There the "P" values are (x,y) pairs, so just apply the equation once for x and once for y:

x1 = 2*xc - x0/2 - x2/2
y1 = 2*yc - y0/2 - y2/2

...where (xc,yc) is the point you want it to pass through, (x0,y0) is the start point, and (x2,y2) is the end point. This will give you a Bezier that passes through (xc,yc) at t=0.5.

Heiskell

This seems to be the perfect answer with the right amount of math and text. Using 0.5 for t makes sence and I get the math now. 0.5 for t means that the middle control point will be passed "halfway", right? That is a perfect value for me. Thanks, will accept answer in a while if it solves my problem. t = 0.5 was what was missing. – Milieu

Yes it works and is a very simple solution. t = 0.5 was the qlue I needed. Thanks. – Milieu

Using t=0.5 is indeed a nice choice. It has the property that P1 is the point furthest away from the line through P0 and P2 (respectively that the tangent on the curve through P1 is parallel to the line P0 P2) – Tantalum

I don't understand how this formula, x1 = 2*xc - x0/2 - x2/2 y1 = 2*yc - y0/2 - y2/2 is derived. I asked this question on another thread, #9711116 – Bentonbentonite

@nemo, I would also like any background information possible on where the equations came from. Thanks! – Thickening

@Walkerneo: I am not sure what you are asking... The first equation is just the definition of a quadratic Bezier curve; and the rest all follow from the first by algebra. Are you asking how Bezier decided what equations to use to define his curves? – Heiskell

@Nemo, Sorry, it all looked very confusing 4 hours ago. I've been brushing up on vectors 'n things and the wiki article here really helped: en.wikipedia.org/wiki/B%C3%A9zier_curve. It'd be awesome if you could include that quadratic curve gif in the answer. I'm still mystified by the mathematics that makes it work, but I suppose that's a whole 'nother problem. – Thickening

P0 and P2 are swapped. It is not a problem, it just means that P(0) equals to P2, and not to P0. – Eldreda

The parameter t is sometimes convenient to compute dynamically. You can use, for example, the ratio of the Euclidean distance from the first point (P0) to the central point (Pc) to the sum of the distances from the central point to the boundary points (P0 and P2). – Jilly

A similar question is that given the quadrative curve y=axx+b*x+c and P0, P2(P0 & P2 are on the cuve), how to find P1. – Ked

Answer 2

Let the quad bezier we want to take as P(t) = P1t^2 + PC2t(1-t) + P2*(1-t)^2 and that quad bezier passing throw P1,Pt,P2

The best quad bezier that pass through the three points P1,Pt,P3 have the control point PC with tension directed in the perpendicular of the tangent of the curve. That point is also bisector of that bezier. Any bezier starting P1 and ending P3 with PC on the rect line that pass throw PC and Pt cuts the quad beziers at the same parametric t value.

The PC point is not achieved through the parametric position t=.5 of the bezier. In general for any P1,Pt,P2 the we got a Pc as described on the next formula.

The resulting PC is also the near point of that bezier to Pt and the rect line that pass through Pt and Pc is the bisector of the triangle P1, Pt, Pc.

Here is the paper where the theorem and formula is described -That is at my website https://microbians.com/math/Gabriel_Suchowolski_Quadratic_bezier_through_three_points_and_the_-equivalent_quadratic_bezier_(theorem)-.pdf

And also here is code

(function() {

    var canvas, ctx, point, style, drag = null, dPoint;

    // define initial points
    function Init() {
        point = {
            p1: { x:200, y:350 },
            p2: { x:600, y:350 }
        };
        point.cp1 = { x: 500, y: 200 };
        
        // default styles
        style = {
            curve:  { width: 2, color: "#333" },
            cpline: { width: 1, color: "#C00" },
            curve1: { width: 1, color: "#2f94e2" },
            curve2: { width: 1, color: "#2f94e2" },
            point: { radius: 10, width: 2, color: "#2f94e2", fill: "rgba(200,200,200,0.5)", arc1: 0, arc2: 2 * Math.PI }
        }
        
        // line style defaults
        ctx.lineCap = "round";
        ctx.lineJoin = "round";

        // event handlers
        canvas.onmousedown = DragStart;
        canvas.onmousemove = Dragging;
        canvas.onmouseup = canvas.onmouseout = DragEnd;
        
        DrawCanvas();
    }
    
    
    // draw canvas
    function DrawCanvas() {
        ctx.clearRect(0, 0, canvas.width, canvas.height);
        
        // control lines
        ctx.lineWidth = style.cpline.width;
        ctx.strokeStyle = style.cpline.color;
        ctx.beginPath();
        ctx.moveTo(point.p1.x, point.p1.y);
        ctx.lineTo(point.cp1.x, point.cp1.y);
        ctx.lineTo(point.p2.x, point.p2.y);
        ctx.stroke();
        
        // curve
        ctx.lineWidth = style.curve.width;
        ctx.strokeStyle = style.curve.color;
        ctx.beginPath();
        ctx.moveTo(point.p1.x, point.p1.y);

        through = !document.getElementById("cbThrough").checked;
        if(through)
        {
            tmpx1 = point.p1.x-point.cp1.x;
            tmpx2 = point.p2.x-point.cp1.x;
            tmpy1 = point.p1.y-point.cp1.y;
            tmpy2 = point.p2.y-point.cp1.y;
            dist1 = Math.sqrt(tmpx1*tmpx1+tmpy1*tmpy1);
            dist2 = Math.sqrt(tmpx2*tmpx2+tmpy2*tmpy2);
            tmpx = point.cp1.x-Math.sqrt(dist1*dist2)*(tmpx1/dist1+tmpx2/dist2)/2;
            tmpy = point.cp1.y-Math.sqrt(dist1*dist2)*(tmpy1/dist1+tmpy2/dist2)/2;
            ctx.quadraticCurveTo(tmpx, tmpy, point.p2.x, point.p2.y);
        }
        else
        {
            ctx.quadraticCurveTo(point.cp1.x, point.cp1.y, point.p2.x, point.p2.y);
        }
        
        ctx.stroke();
        
        //new, t range is [0, 1]
        ctx.beginPath();
        ctx.lineWidth = style.curve1.width;
        ctx.strokeStyle = style.curve1.color;
        
        ctx.moveTo(point.p1.x, point.p1.y);
        
        // control points
        for (var p in point) {
            ctx.lineWidth = style.point.width;
            ctx.strokeStyle = style.point.color;
            ctx.fillStyle = style.point.fill;
            ctx.beginPath();
            ctx.arc(point[p].x, point[p].y, style.point.radius, style.point.arc1, style.point.arc2, true);
            ctx.fill();
            ctx.stroke();
        }
    }
    
    // start dragging
    function DragStart(e) {
        e = MousePos(e);
        var dx, dy;
        for (var p in point) {
            dx = point[p].x - e.x;
            dy = point[p].y - e.y;
            if ((dx * dx) + (dy * dy) < style.point.radius * style.point.radius) {
                drag = p;
                dPoint = e;
                canvas.style.cursor = "move";
                return;
            }
        }
    }
    
    
    // dragging
    function Dragging(e) {
        if (drag) {
            e = MousePos(e);
            point[drag].x += e.x - dPoint.x;
            point[drag].y += e.y - dPoint.y;
            dPoint = e;
            DrawCanvas();
        }
    }
    
    
    // end dragging
    function DragEnd(e) {
        drag = null;
        canvas.style.cursor = "default";
        DrawCanvas();
    }

    
    // event parser
    function MousePos(event) {
        event = (event ? event : window.event);
        return {
            x: event.pageX - canvas.offsetLeft,
            y: event.pageY - canvas.offsetTop
        }
    }
    
    
    // start
    canvas = document.getElementById("canvas");
    if (canvas.getContext) {
        ctx = canvas.getContext("2d");
        Init();
    }
    
})();

 

html, body { background-color: #DDD;font-family: sans-serif; height: 100%; margin:0;
padding:10px;
}
canvas { display:block;}
#btnControl { font-size:1em; position: absolute; top: 10px; left: 10px; }
#btnSplit { font-size:1em; position: absolute; top: 35px; left: 10px; }
#text { position: absolute; top: 75px; left: 10px; }
a {
  text-decoration: none;
  font-weight:700;
  color: #2f94e2;
}
#little { font-size:.7em; color:#a0a0a0; position: absolute; top: 775px; left: 10px; }

<h1>Quadratic bezier throw 3 points</h1>
<div>
  
  Also take a look the the math paper <a target="_blank" href="https://microbians.com/mathcode">Quadratic bezier through three points! →</a> <br/><br/>
  Gabriel Suchowolski (<a href="https://microbians.com" target="_blank">microbians</a>), December, 2012
</div>
<div id="little">Thanks to 艾蔓草 xhhjin for the code (that I fork) implementing my math paper.</div>
  <br/>
</div>
<input type="checkbox" id="cbThrough" name="through"/>Primitive quadratic Bezier (as control points)</input><br/><br/>
<canvas id="canvas" height="500" width="800" class="through" style="cursor: default; background-color: #FFF;"></canvas>

Enjoy

Hostel

Excellent answer and a very cool website I must say 👍 – Bergamot

Thank you very much. I have been working on curved line feature approximately 2 weeks. I've used copilot, gpt 3.5, gemini etc. I made many researches on numerous website included stackoverflow. Only this solution worked precisely in my end. I am curious do you have any formula like this for cubic bezier curves? The algorithm which I tried by now not worked great at all. Thank you in advance. – Eldreeda

Sorry I only made this research for the quadratic case. Happy it helps you. – Hostel

Answer 3

I have used Nemos answer in my JavaFX apllication, but my goal was to draw the curve, so that the visual turning point of the curve always fits with the choosen fixed one (CP).

CP = ControlPoint
SP = StartPoint
EP = EndPoint
BP(t) = variable Point on BeziérCurve where t is between 0 and 1

To achieve this i made a variable t (not fix 0.5). If the choosen Point CP is no longer in the middle between SP and EP, you have to vary t up or down a little bit. As a first step you need to know if CP is closer to SP or EP: Let distanceSP be the distance between CP and SP and distanceEP the distance between CP and EP then i define ratio as:

ratio = (distanceSP - distanceEP) / (distanceSP + distanceEP);

Now we are going to use this to vary t up and down:

ratio = 0.5 - (1/3) * ratio;

note: This is still an approximation and 1/3 is choosen by try and error.

Here is my Java-Function: (Point2D is a class of JavaFX)

private Point2D adjustControlPoint(Point2D start, Point2D end, Point2D visualControlPoint) {
    // CP = ControlPoint, SP = StartPoint, EP = EndPoint, BP(t) = variable Point on BeziérCurve where t is between 0 and 1
    // BP(t) = SP*t^2 + CP*2*t*(1-t) + EP*(1-t)^2
    // CP = (BP(t) - SP*t^2 - EP*(1-t)^2) / ( 2*t*(1-t) )
    // but we are missing t the goal is to approximate t
    double distanceStart  = visualControlPoint.distance(start);
    double distanceEnd    = visualControlPoint.distance(end);
    double ratio          = (distanceStart - distanceEnd) / (distanceStart + distanceEnd);
    // now approximate ratio to be t
    ratio = 0.5 - (1.0 / 3) * ratio;

    double ratioInv = 1 - ratio;
    Point2D term2 = start.multiply( ratio * ratio );
    Point2D term3 = end.multiply( ratioInv * ratioInv );
    double  term4 = 2 * ratio * ratioInv;

    return visualControlPoint.subtract(term2).subtract(term3).multiply( 1 / term4);
}

I hope this helps.

Malcommalcontent

Answer 4

If you don't want the exact middle point, rather you want any value for t (0 to 1), the equation is:

controlX = pointToPassThroughX/t - startX*t - endX*t;
controlY = pointToPassThroughY/t - startY*t - endY*t;

Of course, this will also work for the mid point, just set t to be 0.5. Simple! :-)

Edmanda

I think that should be controlX = pointToPassThroughX/(2*t*(1-t))-startX*t/(2*(1-t))-endX*(1-t)/(2*t). – Sackville