Find coordinate of the closest point on polygon in Shapely

Question

Say I have the following Polygon and Point:

>>> poly = Polygon([(0, 0), (2, 8), (14, 10), (6, 1)])
>>> point = Point(12, 4)

I can calculate the point's distance to the polygon...

>>> dist = point.distance(poly)
>>> print(dist)
2.49136439561

...but I would like to know the coordinate of the point on the polygon border where that shortest distance measures to.

My initial approach is to buffer the point by its distance to the polygon, and find the point at which that circle is tangent to the polygon:

>>> buff = point.buffer(dist) 

However, I'm not sure how to calculate that point. The two polygon's don't intersect so list(poly.intersection(buff)) will not give me that point.

Am I on the right track with this? Is there a more straightforward method?

Hilel

Duplicate? #10984372 – Dollop

@Oleg, I don't believe this is a duplicate. As I mention above, I have no issue calculating the minimum distance to the polygon. I'm trying to find the point on the polygon boundary where that minimum distance is measured to. – Hilel

Possible duplicate of Coordinates of the closest points of two geometries in Shapely – Illfounded

Answer 1

Please, do not up-vote this answer, the correct answer is @Georgy 's answer below.

My answer for reference:

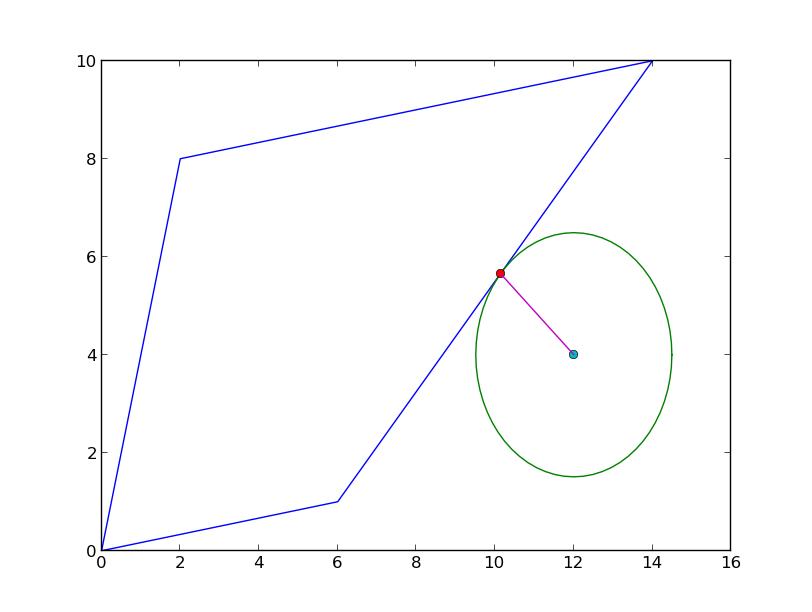
There is an easy way to do this relying on Shapely functions. First, you need to get the exterior ring of the polygon and project the point to the ring. It is mandatory to get the exterior as a LinearRing since polygons do not have the projection function. Opposed to intuition, this gives a distance, the distance from the first point of the ring to the point in the ring closest to the given point. Then, you just use that distance to get the point with the interpolate function. See the code below.

from shapely.geometry import Polygon, Point, LinearRing

poly = Polygon([(0, 0), (2,8), (14, 10), (6, 1)])
point = Point(12, 4)

pol_ext = LinearRing(poly.exterior.coords)
d = pol_ext.project(point)
p = pol_ext.interpolate(d)
closest_point_coords = list(p.coords)[0]

It is important to mention that this method only works if you know the point is outside the exterior of the polygon. If the point is inside one of its interior rings, you need to adapt the code for that situation.

If the polygon doesn't have interior rings, the code will work even for points inside the polygon. That is because we are in fact working with the exterior ring as a line string, and ignoring whether the line string comes from a polygon or not.

It is easy to extend this code to the general case of computing the distance of any point (inside or outside of the polygon) to the closest point in the polygon boundary. You only need to compute the closest point (and distance) from the point to all line rings: the exterior ring, and each interior ring of the polygon. Then, you just keep the minimum of those.

Susiesuslik

this is perfect. I was not familiar with those Shapely functions. Can this also work if the exterior point was instead a polygon? I tried using pol_ext.project() to both a polygons and to a linestring, but get the error message "third argument of GEOSProject_r must be Point*". Any suggestions on this? – Hilel

Not that I know. I think for that you have no choice other than implementing something yourself. Tome Karzes answer can be easily addapted to that scenario (but using one of the polygons as "the point", since you have the above method). – Susiesuslik

In the answer of the question #38515107 you can find an implementation of Tom Karzes suggested algorithm to get the distance between two not crossing linestrings. The code there can be easily adapted to get the distance between a linestring and a point, and does not depend on shapely functions. – Susiesuslik

Thanks, this is helpful. Can you perhaps go into more detail as to why it doesn't work when the point is inside the polygon? I ran this code a couple times with different points, and the result looked like it was correct. – Cholecystotomy

Sure. I'll complete the answer. I assume your polygons do not have interior rings, in that case, the code will indeed work. – Susiesuslik

Answer 2

While the answer of eguaio does the job, there is a more natural way to get the closest point using shapely.ops.nearest_points function:

from shapely.geometry import Point, Polygon
from shapely.ops import nearest_points

poly = Polygon([(0, 0), (2, 8), (14, 10), (6, 1)])
point = Point(12, 4)
# The points are returned in the same order as the input geometries:
p1, p2 = nearest_points(poly, point)
print(p1.wkt)
# POINT (10.13793103448276 5.655172413793103)

The result is the same as in the other answer:

from shapely.geometry import LinearRing
pol_ext = LinearRing(poly.exterior.coords)
d = pol_ext.project(point)
p = pol_ext.interpolate(d)
print(p.wkt)
# POINT (10.13793103448276 5.655172413793103)
print(p.equals(p1))
# True

Illfounded

This should be the correct answer now. This function was not available at the time I wrote the original answer. It seems I should re-read the library documentation now. – Susiesuslik

@Susiesuslik Version history and GitHub say that nearest_points was added in 2014, though. – Illfounded

I should read the documentation more carefully then! @Illfounded thank you for the contribution. – Susiesuslik

If your point is inside the polygon you can use: p1, p2 = nearest_points(poly.boundary, point) – Angleaangler

@Illfounded - Need your help to get the distance between the farthest point of a polygon to a point outside the polygon. (lat lon given) – Normand

@ZeeshanEqbal This should answer your question: Find longest “straight” path between Point and Polygon – Illfounded

@Illfounded Thanks for your quick response. But will it work with latitude and long? – Normand

@ZeeshanEqbal Depends on what units you expect the result to have, I suppose. The answer to the question I linked says that you will have to first convert the coordinates. Unfortunately, I'm not the best person to help with that. :) See the links under that answer. Maybe there is something useful there. – Illfounded

Note: if the point is inside the polygon, nearest_points will simply return the point value. Applying nearest_points to the boundary of the polygon (poly.boundary) seems to work regardless of whether the point is inside or out. – Runabout

Answer 3

I liked the idea of intersecting the polygon poly with a circle buff centered at the point point, just as you wrote in your question. I would suggest: poly.boundary.intersection(buff.boundary)

Gilbert