Distance from a point to a polygon

Question

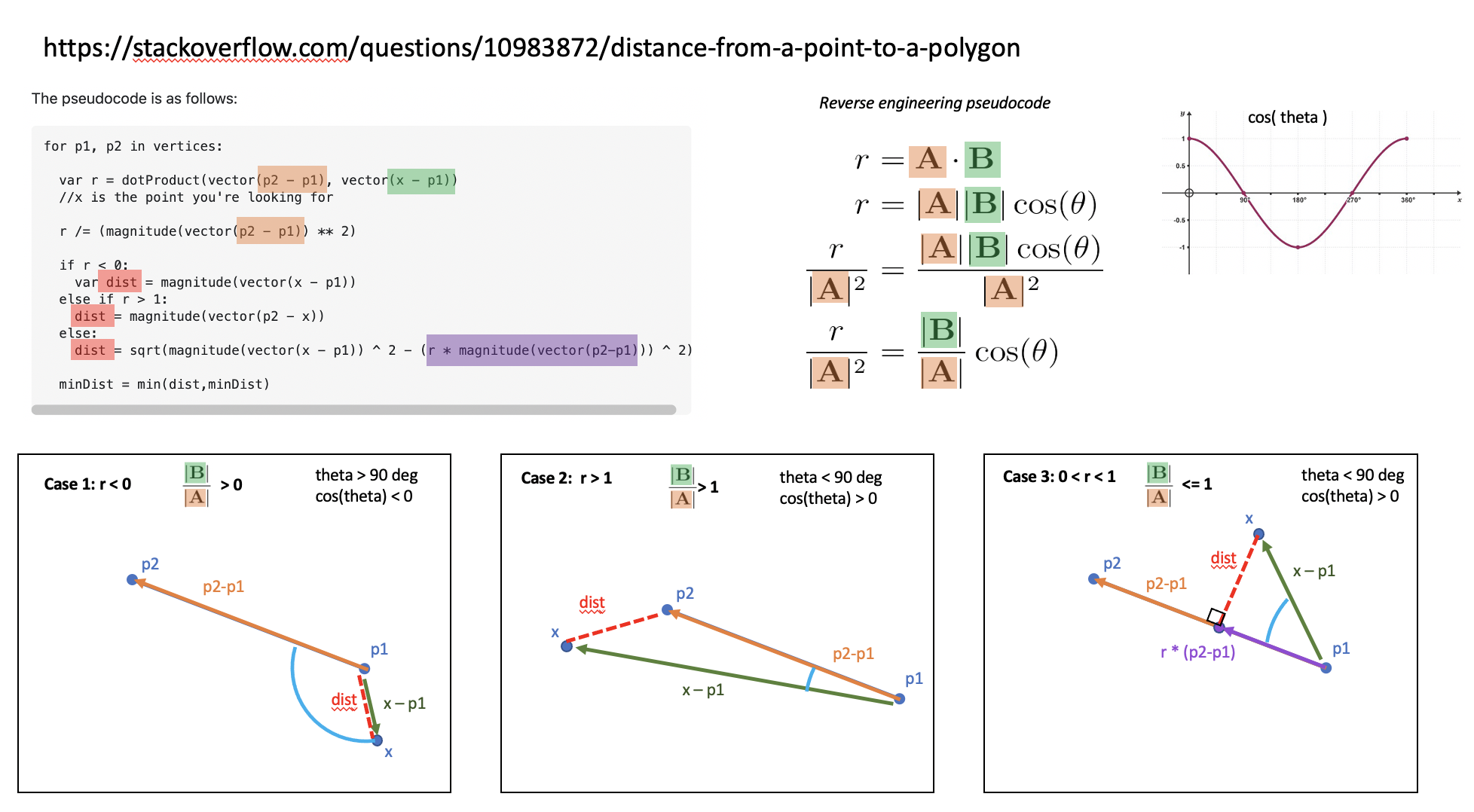
I am trying to determine the distance from a point to a polygon in 2D space. The point can be inside or outside the polygon; The polygon can be convex or concave.

If the point is within the polygon or outside the polygon with a distance smaller than a user-defined constant d, the procedure should return True; False otherwise.

I have found a similar question: Distance from a point to a polyhedron or to a polygon. However, the space is 2D in my case and the polygon can be concave, so it's somehow different from that one.

I suppose there should be a method simpler than offsetting the polygon by d and determining it's inside or outside the polygon.

Any algorithm, code, or hints for me to google around would be appreciated.

Miserere

Does the calling code need to know the distance, or just whether it is within a certain distance? – Councilwoman

I found this for you. It returns the actual distance from point to polygon (positive if the point is outside the polygon and negative otherwise). It's Matlab code but may be helpful from an algorithmic perspective: mathworks.com/matlabcentral/fileexchange/… – Paralyse

@KendallFrey just whether it is within a certain distance. However, would it be possible to determine whether it's within a certain distance without knowing exactly what the distance is? – Miserere

Does it matter what point on the polygon, can it be on part of the line connecting 2 points? Are you looking for minimum distance, or simply ANY distance? – Craze

@Craze looking for minimum distance. Sorry not sure about what you mean by "part of the line connecting 2 points". Any point on the boundary of the polygon counts. – Miserere

@GirishRao thanks. Does the code implement a certain algorithm? I'll try to google around for a Python version. – Miserere

From the looks of it, the code given by GirishRao implements the idea given in the answers. – Bare

@Miserere - what I meant is, if the problem was as simple as testing the distances from your given point, to the point vertices that make up the polygon, or whether it could be to any point on any line connecting 2 vertices? – Craze

possible duplicate of Distance from a point to a polyhedron or to a polygon – Focus

Answer 1

Your best bet is to iterate over all the lines and find the minimum distance from a point to a line segment.

To find the distance from a point to a line segment, you first find the distance from a point to a line by picking arbitrary points P1 and P2 on the line (it might be wise to use your endpoints). Then take the vector from P1 to your point P0 and find (P2-P1) . (P0 - P1) where . is the dot product. Divide this value by ||P2-P1||^2 and get a value r.

Now if you picked P1 and P2 as your points, you can simply check if r is between 0 and 1. If r is greater than 1, then P2 is the closest point, so your distance is ||P0-P2||. If r is less than 0, then P1 is the closest point, so your distance is ||P0-P1||.

If 0<r<1, then your distance is sqrt(||P0-P1||^2 - (r * ||P2-P1||)^2)

The pseudocode is as follows:

for p1, p2 in vertices:

  var r = dotProduct(vector(p2 - p1), vector(x - p1))
  //x is the point you're looking for

  r /= (magnitude(vector(p2 - p1)) ** 2)

  if r < 0:
    var dist = magnitude(vector(x - p1))
  else if r > 1:
    dist = magnitude(vector(p2 - x))
  else:
    dist = sqrt(magnitude(vector(x - p1)) ^ 2 - (r * magnitude(vector(p2-p1))) ^ 2)

  minDist = min(dist,minDist)

Shoe

This is what I thinking as well. This SO answer talks about finding the shortest distance between a point and a line segment: #849711 . – Indoxyl

is there any algo available for that? – Pasture

@Muneem I updated my answer for easy to understand pseudocode at the end. – Shoe

I believe there are a couple of errors in the description and code: r should be divided by the squared magnitude of P1P2, not the magnitude of PP1. Haven't checked the math, but that's consistent with the answer linked to in the comment by @hatchet, and that works much better! – Hypogeous

First, you also need to check if the point is in the polygon. If so, return zero, otherwise follow @HansZ calculation – Replica

Answer 2

In the event that this helps someone else, I reverse engineered doverbin's answer to understand why it worked showing graphically what the three cases are computing. (doverbin, feel free to incorporate this into your answer if you wish.)

Glavin

Answer 3

If you have a working point to line segment distance function, you can use it to calculate the distance from the point to each of the edges of the polygon. Of course, you have to check if the point is inside the polygon first.

Bare

Answer 4

Do you need fast or simple?
Does it have to be always absolutely correct in edge cases or will good enough most of the time be OK?

Typical solution are to find the distance to each vertex and find the pair with the smallest values ( note that for a point outside a convex polygon these might not be adjacent) and then check point to line intersections for each segment.

For large complex shapes you can also store approx polygon bounding boxes (either rectangular or hexagons) and find the closest side before checking more detail.

You may also need code to handle the special case of exactly on a line.

Gliadin

Consider the extreme example of a triangle polygon with two vertices very distant from the target point, but with the line between them passing very close to the target point. The third vertex of the triangle is just a short distance beyond that line. A shortcut that only examines lines connected to that closest vertex will produce the wrong answer. – Indoxyl

@hatchet, yes that's why I said you need to consider the use. A collision detection routine in a game is different from navigation and a fractal coastline is different from a CFD app. – Gliadin

I program games, this algorithm seems unsound for any application in which the edges of the polygon are not guaranteed to be of equal length. – Milton

To elaborate for others just finding this. I think this solution 'bounding box' is a good solution for a collision broad phase. But if you are dealing with distance, i.e. trying to find the closest of one of several polygons to a point, it does not help at all. This is because you can always contrive a polygon which generates a bounding box that is closer to a point but with an actual boundary that is further. – Tacket

Answer 5

I can help you with this pointers:

• The distance can be calculated using Wikipedia entry, even with an untested snipped of code.
• The inside/outside border can be solved with this Stack Post and links

and some remarks:

• you should check only the nearest points, as Martin Beckett´s answer point outs, since another segment can "proyected" very near, but in reality don´t be close as need.

Ectophyte

For inside/outside border problem, I am not comparing only to rectangles, but general polygons. I found the comment in the link you gave helps though. Thanks! – Miserere

Answer 6

I do not know about the difference in performance with respect to the rest of answers, but in boost C++ libraries there is an generic implementation called distance. It has information about complexity in every case and in your problem case it is linear.

I was also looking for solutions to this problem some days ago and I want to share this finding. Hope it helps to someone.

Gigantism