scikit-learn: Predicting new points with DBSCAN

Question

I am using DBSCAN to cluster some data using Scikit-Learn (Python 2.7):

from sklearn.cluster import DBSCAN
dbscan = DBSCAN(random_state=0)
dbscan.fit(X)

However, I found that there was no built-in function (aside from "fit_predict") that could assign the new data points, Y, to the clusters identified in the original data, X. The K-means method has a "predict" function but I want to be able to do the same with DBSCAN. Something like this:

dbscan.predict(X, Y)

So that the density can be inferred from X but the return values (cluster assignments/labels) are only for Y. From what I can tell, this capability is available in R so I assume that it is also somehow available in Python. I just can't seem to find any documentation for this.

Also, I have tried searching for reasons as to why DBSCAN may not be used for labeling new data but I haven't found any justifications.

Marry

Answer 1

Clustering is not classification.

Clustering is unlabeled. If you want to squeeze it into a prediction mindset (which is not the best idea), then it essentially predicts without learning. Because there is no labeled training data available for clustering. It has to make up new labels for the data, based on what it sees. But you can't do this on a single instance, you can only "bulk predict".

But there is something wrong with scipys DBSCAN:

random_state : numpy.RandomState, optional :

The generator used to initialize the centers. Defaults to numpy.random.

DBSCAN does not "initialize the centers", because there are no centers in DBSCAN.

Pretty much the only clustering algorithm where you can assign new points to the old clusters is k-means (and its many variations). Because it performs a "1NN classification" using the previous iterations cluster centers, then updates the centers. But most algorithms don't work like k-means, so you can't copy this.

If you want to classify new points, it is best to train a classifier on your clustering result.

What the R version maybe is doing, is using a 1NN classificator for prediction; maybe with the extra rule that points are assigned the noise label, if their 1NN distance is larger than epsilon, mabye also using the core points only. Maybe not.

Get the DBSCAN paper, it does not discuss "prediction" IIRC.

Kopp

Scikit-learn's k-means clustering has a method to "predict": predict(X): Predict the closest cluster each sample in X belongs to., and that's typically what one intends to do with "prediction" in the clustering context. – Klingel

@Klingel except that only for k-means "closest" makes any sense, and will be consistent with the cluster labels. With DBSCAN, this will not produce the same labels as fit_predict, i.e., it will be inconsistent. – Kopp

Answer 2

While Anony-Mousse has some good points (Clustering is indeed not classifying) I think the ability of assigning new points has it's usefulness. ^*

Based on the original paper on DBSCAN and robertlaytons ideas on github.com/scikit-learn, I suggest running through core points and assigning to the cluster of the first core point that is within eps of you new point. Then it is guaranteed that your point will at least be a border point of the assigned cluster according to the definitions used for the clustering. (Be aware that your point might be deemed noise and not assigned to a cluster)

I've done a quick implementation:

import numpy as np
import scipy as sp

def dbscan_predict(dbscan_model, X_new, metric=sp.spatial.distance.cosine):
    # Result is noise by default
    y_new = np.ones(shape=len(X_new), dtype=int)*-1 

    # Iterate all input samples for a label
    for j, x_new in enumerate(X_new):
        # Find a core sample closer than EPS
        for i, x_core in enumerate(dbscan_model.components_): 
            if metric(x_new, x_core) < dbscan_model.eps:
                # Assign label of x_core to x_new
                y_new[j] = dbscan_model.labels_[dbscan_model.core_sample_indices_[i]]
                break

    return y_new

The labels obtained by clustering (dbscan_model = DBSCAN(...).fit(X) and the labels obtained from the same model on the same data (dbscan_predict(dbscan_model, X)) sometimes differ. I'm not quite certain if this is a bug somewhere or a result of randomness.

EDIT: I Think the above problem of differing prediction outcomes could stem from the possibility that a border point can be close to multiple clusters. Please update if you test this and find an answer. Ambiguity might be solved by shuffling core points every time or by picking the closest instead of the first core point.

*) Case at hand: I'd like to evaluate if the clusters obtained from a subset of my data makes sense for other subset or is simply a special case. If it generalises it supports the validity of the clusters and the earlier steps of pre-processing applied.

Yetac

is it possible to predict new data points with agglomerative clustering? – Gaff

Possible yes, but I think the above concerns are at least as relevant. In the above case I exploited that DBSCAN has a notion of closeness. IIRC Aglo. Clustering doesn't, so you have to introduce a new one, e.g. a K-NN inspired one. I suggest really paying attention to @anony-mousse 's answer. – Yetac

From sklearn's user guide: even though the core samples will always be assigned to the same clusters, the labels of those clusters will depend on the order in which those samples are encountered in the data. Second and more importantly, the clusters to which non-core samples are assigned can differ depending on the data order. – Tithable

Answer 3

Here a slightly different and more efficient implementation. Also, instead of taking the first best core point that is within the eps radius, the core point that is closest to the sample is taken.

def dbscan_predict(model, X):

    nr_samples = X.shape[0]

    y_new = np.ones(shape=nr_samples, dtype=int) * -1

    for i in range(nr_samples):
        diff = model.components_ - X[i, :]  # NumPy broadcasting

        dist = np.linalg.norm(diff, axis=1)  # Euclidean distance

        shortest_dist_idx = np.argmin(dist)

        if dist[shortest_dist_idx] < model.eps:
            y_new[i] = model.labels_[model.core_sample_indices_[shortest_dist_idx]]

    return y_new

Jobyna

Great function! The only think I would change, assuming X is a pandas.DataFrame: diff = model.components_ - list(X.iloc[i, :]) – Lovage

Answer 4

Although it's not the exact same algorithm you can preform approximate predictions for new points with sklearn HDBSCAN. See here.

It works like this:

clusterer = hdbscan.HDBSCAN(min_cluster_size=15, prediction_data=True).fit(data)
test_labels, strengths = hdbscan.approximate_predict(clusterer, test_points)

Avelinaaveline

This (might) produce way different resutlts than DBSCAN. I got some (insanely) great results using DBSCAN, but I cannot label new points - unfortunately HDBSCAN does not produce the same quality of results (or atleast I can't make it) – Kindergartner

Answer 5

Great answers are already posted to this question here. My suggestion is to give HDBSCAN a try. It provides an approximate_predict() method which might be what you need.

Excitability

add an detailed explanation of how this will solve the problem – Dormouse

Answer 6

Let's first try to understand a few basic things about DBSCAN density-based clustering, the following figure summarizes the basic concepts.

Let's first create a sample 2D dataset that will be clustered with DBSCAN. The following figure shows how the dataset looks.

import numpy as np
import matplotlib.pylab as plt
from sklearn.cluster import DBSCAN

X_train = np.array([[60,36], [100,36], [100,70], [60,70],
    [140,55], [135,90], [180,65], [240,40],
    [160,140], [190,140], [220,130], [280,150], 
    [200,170], [185, 170]])
plt.scatter(X_train[:,0], X_train[:,1], s=200)
plt.show()

Now let's use scikit-learn's implementation of DBSCAN to cluster:

eps = 45
min_samples = 4
db = DBSCAN(eps=eps, min_samples=min_samples).fit(X_train)
labels = db.labels_
labels
# [ 0,  0,  0,  0,  0,  0,  0, -1,  1,  1,  1, -1,  1,  1]
db.core_sample_indices_
# [ 1,  2,  4,  9, 12, 13]

Notice from the above results that

• there are 6 core points found by the algorithm
• 2 clusters (with labels 0, 1) and couple of outliers (noise points) are found.

Let's visualize the clusters using the following code snippet:

def dist(a, b):
    return np.sqrt(np.sum((a - b)**2))

colors = ['r', 'g', 'b', 'k']
for i in range(len(X_train)):
    plt.scatter(X_train[i,0], X_train[i,1], 
                s=300, color=colors[labels[i]], 
                marker=('*' if i in db.core_sample_indices_ else 'o'))
                                                            
    for j in range(i+1, len(X_train)):
        if dist(X_train[i], X_train[j])  < eps:
            plt.plot([X_train[i,0], X_train[j,0]], [X_train[i,1], X_train[j,1]], '-', color=colors[labels[i]])
            
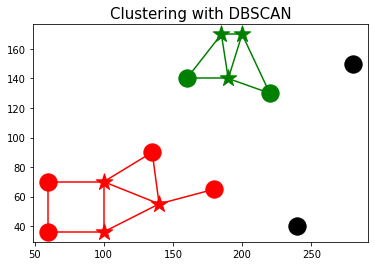
plt.title('Clustering with DBSCAN', size=15)
plt.show()

• points in cluster 0 are colored red
• points in cluster 1 are colored green
• outlier points are colored black
• core points are marked with '*'s.
• two points are connected by an edge if they are within ϵ-nbd.

Finally, let's implement the predict() method to predict the cluster of a new data point. The implementation is based on the following:

• in order that the new point x belongs to a cluster, it must be directly density reachable from a core point in the cluster.

• We shall compute the nearest core point to the cluster, if it's within ϵ distance from x, we shall return the label of the core point, otherwise the point x will be declared a noise point (outlier).

• Notice that this differs from the training algorithm, since we no longer allow any more point to become a new core point (i.e., number of core points are fixed).

• the next code snippet implements the predict() function based on the above idea

  def predict(db, x):
    dists = np.sqrt(np.sum((db.components_ - x)**2, axis=1))
    i = np.argmin(dists)
    return db.labels_[db.core_sample_indices_[i]] if dists[i] < db.eps else -1
  
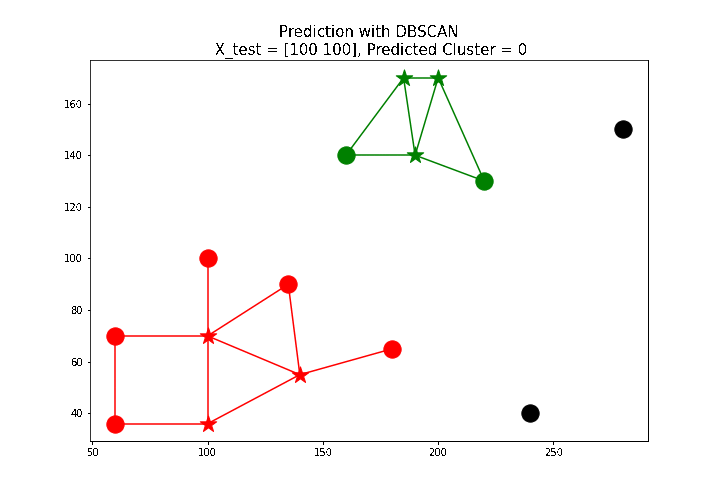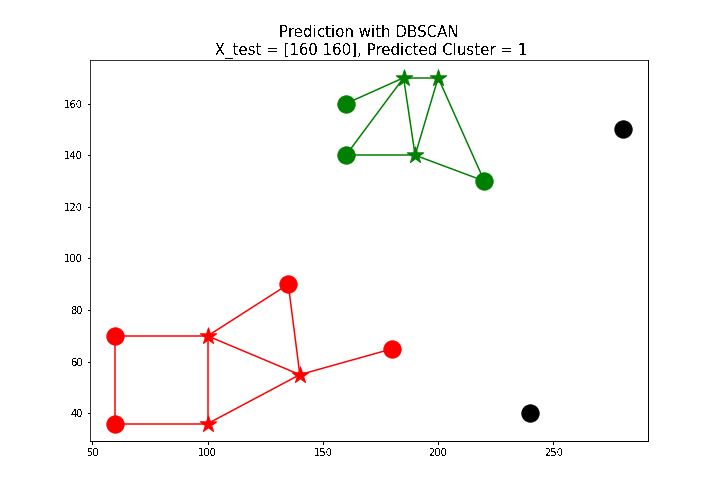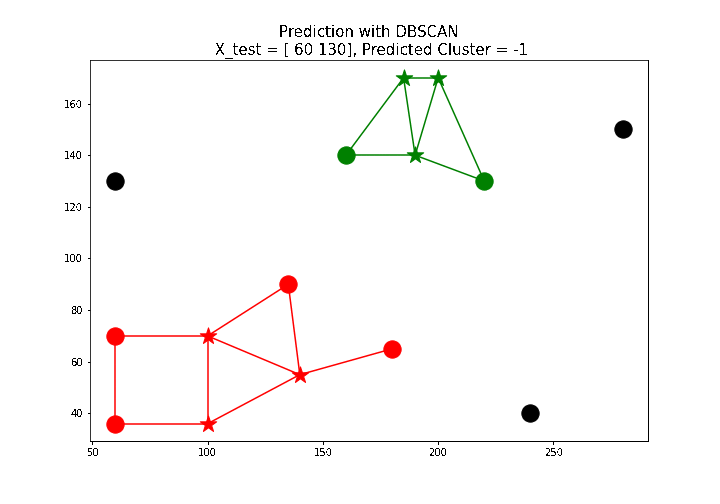
  X_test = np.array([[100, 100], [160, 160], [60, 130]])
  for i in range(len(X_test)):
     print('test point: {}, predicted label: {}'.format(X_test[i], 
                                                 predict(db, X_test[i])))
  # test point: [100 100], predicted label: 0
  # test point: [160 160], predicted label: 1
  # test point: [ 60 130], predicted label: -1
  

The next animation shows how a few new test points are labeled using the predict() function defined above.

Roughspoken

Answer 7

Non-parametric clustering models like DBSCAN, Spectral clustering, and Hierarchical clustering, cannot directly predict labels of new points, because they are non-parametric. That means we cannot get a set of parameters, and predict the label of a new point based on the parameters.

As a comparison, K-means and Gaussian mixture model are parametric clustering models.

The Clustering with Neural Network and Index (CNNI) model is another parametric clustering model.

To predict labels of new points after analysis of DBSCAN, as other answers' suggestion, we may need to train a supervised model with the clustering result, then predict the label with the supervised model. Or just using the KNN classifier.

Min-Max-Jump distance provides an alternative method for predicting labels of new points.

https://doi.org/10.31219/osf.io/fbxrz

To predict label of a new point, we just compare the point's Min-Max-Jump distance to the center (One-SCOM) of each cluster. A mechanism that is similar to K-means.

Following is an example of using Min-Max-Jump distance to predict labels of 10,000 new points, of three toy data-sets.

Predicting labels of new points

Here is an example illustrating difference between KNN and Min-Max-Jump distance to predict labels of new points, when the clusters are not well separated.

Pandolfi

Answer 8

The K-means algo doesn't do prediction, it just tries to best place the K clusters. sklearn.cluster.KMeans.predict compares the Euclidian distance of each cluster to the new instance and labels it with the closest cluster.

DBSCAN doesn't have cluster centers, but it does have one or more "core instances" per cluster.

Therefore, some prediction options after using DBSCAN are:

• Make a function to select the core cluster with the smallest distance to a new instance, and then label that instance with the cluster that this "closest core instance" belongs to.
• Use the unlabeled input data to the DBSCAN model + cluster labels from sklearn.cluster.DBSCAN.fit.labels_ as labels to train a supervised machine learning model, and then feed that model your new instances to predict the cluster that they belong to.

--An aside--

To help avoid confusion (as I've seen some answers say some wrong things), it is true that DBSCAN is non-parametric, but that is not why sklearn's implementation has no predict function.

As a counter example, k-Nearest Neighbors is non-parametric and is capable of making predictions.

Regicide

Answer 9

DBSCAN.fit_predict(X, y=None, sample_weight=None)

Read more information from https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html

Timothytimour

This does a new fit. Careful! – Gestalt