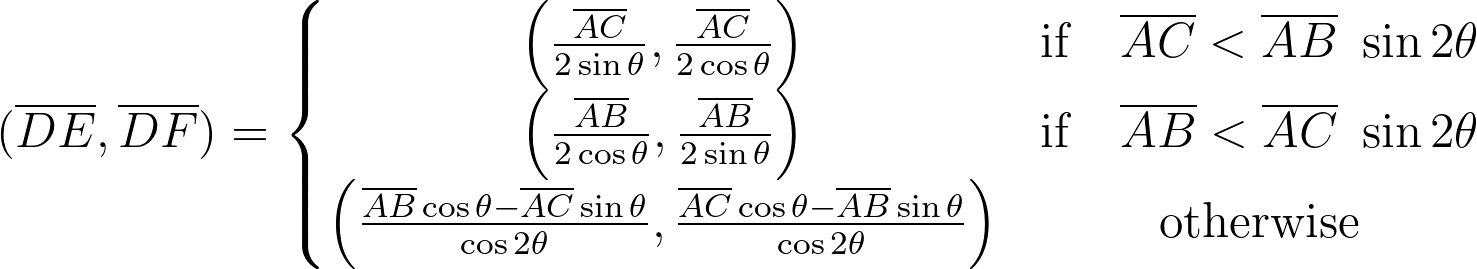Calculate largest inscribed rectangle in a rotated rectangle

Question

I'm trying to find the best way to calculate the biggest (in area) rectangle which can be contained inside a rotated rectangle.

Some pictures should help (I hope) in visualizing what I mean:

The width and height of the input rectangle is given and so is the angle to rotate it. The output rectangle is not rotated or skewed.

I'm going down the longwinded route which I'm not even sure if it will handle the corner cases (no pun intended). I'm certain there is an elegant solution to this. Any tips?

EDIT: The output rectangle points don't necessarily have to touch the input rectangles edges. (Thanks to Mr E)

Builder

By "biggest rectangle", do you mean the one with the largest area? – Agnew

@Sven yes, thats what is meant. I'll do an edit...Thanks. – Builder

@George Profenza the only other option was to write three thousand words... – Builder

Does it always exist? I'm not sure it does. Sketch a long and thin rectangle and rotate it. – Arctogaea

Isn't this more of a math problem than a programming one? – Prochronism

@Me E I Yes. An output rectangle of just a single pixel is ok. – Builder

@Builder I mean as in a rectangle where each corner touches a side of the rotated rectangle might not exist. – Arctogaea

should the output rectangle have its sides parallel to the axes? ie. can the output rectangle also be rotated? – Inaugural

@Inaugural parallel to axes. Thats why I mentioned 'not rotated or skewed'. – Builder

@Mr E don't totally get you but thinking of a thin rectangle 'line' then there could be many solutions. hmmm... – Builder

@Builder look at the picture here: i.imgur.com/22yAQ.jpg , perhaps slightly more rotated. How can you fit such a rectangle inside this one? – Arctogaea

@Mr E you are right! so I guess the points belonging to the output rectangle do not have to be on the the input rectangles edges. Will have to make a not of that in the question. – Builder

how is this problem different from #7745 ? – Inaugural

@Inaugural yes, that Dr Dobb's article could shed some light on this problem. If I squeeze my problem into that data structure it would probably work. maybe. – Builder

Answer 1

I just came here looking for the same answer. After shuddering at the thought of so much math involved, I thought I would resort to a semi-educated guess. Doodling a bit I came to the (intuitive and probably not entirely exact) conclusion that the largest rectangle is proportional to the outer resulting rectangle, and its two opposing corners lie at the intersection of the diagonals of the outer rectangle with the longest side of the rotated rectangle. For squares, any of the diagonals and sides would do... I guess I am happy enough with this and will now start brushing the cobwebs off my rusty trig skills (pathetic, I know).

Minor update... Managed to do some trig calculations. This is for the case when the Height of the image is larger than the Width.

Update. Got the whole thing working. Here is some js code. It is connected to a larger program, and most variables are outside the scope of the functions, and are modified directly from within the functions. I know this is not good, but I am using this in an isolated situation, where there will be no confusion with other scripts: redacted

---

I took the liberty of cleaning the code and extracting it to a function:

function getCropCoordinates(angleInRadians, imageDimensions) {
    var ang = angleInRadians;
    var img = imageDimensions;

    var quadrant = Math.floor(ang / (Math.PI / 2)) & 3;
    var sign_alpha = (quadrant & 1) === 0 ? ang : Math.PI - ang;
    var alpha = (sign_alpha % Math.PI + Math.PI) % Math.PI;

    var bb = {
        w: img.w * Math.cos(alpha) + img.h * Math.sin(alpha),
        h: img.w * Math.sin(alpha) + img.h * Math.cos(alpha)
    };

    var gamma = img.w < img.h ? Math.atan2(bb.w, bb.h) : Math.atan2(bb.h, bb.w);

    var delta = Math.PI - alpha - gamma;

    var length = img.w < img.h ? img.h : img.w;
    var d = length * Math.cos(alpha);
    var a = d * Math.sin(alpha) / Math.sin(delta);

    var y = a * Math.cos(gamma);
    var x = y * Math.tan(gamma);

    return {
        x: x,
        y: y,
        w: bb.w - 2 * x,
        h: bb.h - 2 * y
    };
}

I encountered some problems with the gamma-calculation, and modified it to take into account in which direction the original box is the longest.

-- Magnus Hoff

Pastille

Nice graphics. I'll think about this idea. If you manage to produce code then please post it here! – Builder

I am working on the same problem right now. Trying to build a WYSIWYG front-end for some server-based image rotation and cropping. I did some calculations too. Posting them here. As images.... I haven't coded anything yet. – Pastille

I ended up using this. Thank you! In the process I rewrote your code. I posted it as an edit, as I think it is better, but please feel free to revert it or edit it further :) – Shamrao

Whoa, I had almost forgotten about this. Thank you for the rewrite. – Pastille

This function is awesome! I just used it on a project for a hackathon and would have been lost without it. Thank you both! :) – Degrading

Legend. I've tried five different solutions to this problem and this is the only one that works correctly. Btw I converted your function to Python for my application - see https://mcmap.net/q/258295/-rotate-image-and-crop-out-black-borders – Trixie

It's not working correctly for case where width > height. I fixed and optimized it in my answer. – Horizon

Answer 2

Trying not to break tradition putting the solution of the problem as a picture:)

---

Edit: Third equations is wrong. The correct one is:

3.w * cos(α) * X + w * sin(α) * Y - w * w * sin(α) * cos(α) - w * h = 0

To solve the system of linear equations you can use Cramer rule, or Gauss method.

Gendarmerie

How is it possible to put P, Q, R, S to equations 1, 2, 3, and 4? Please give a sample on a substitution into one of the 4 equations. Thank you. – Handwoven

P should be puted in first equation (which is equation of line (A, B)). And because P(x1, y1) is on that line, the x1 and y1 should be such that the equality w * cos(a) * x1 + w * sin(a) * y1 -w * w * sin(a) * cos(a) = 0 holds. – Gendarmerie

@Mihran Hovsepyan thanks for that. I'll look into it and see if I can grok it. – Builder

Mihran - I have updated my answer with a link to a research paper that solves your question. Please see my updated answer below. – Jacklight

Sorry @Jason Moore what question you mean? I have no question here. – Gendarmerie

This solution isn't always correct. For example: if the angle is 45 degrees, then there is no solution with all verteces on the boundaries of the large rectangle unless it's a square. When it is a square, then your equations have infinitely many solutions. – Red

@Jefferey Please give me some example with h = ? w = ? and alpha = ?. – Gendarmerie

@Mihran I already gave you one: alpha=45 degrees and w not equal to h. Then sin a = cos a, and you end up with inconsistent equations. – Red

@Mihran Another problem is evident when alpha is the angle between a side and the diagonal. In that case A, P and S coincide and so do C, Q and R. Your inner rectangle collapses to a line. This is obviously not the rectangle with largest area! – Red

Thank you for pointing the problem @Jeffrey! I will try to solve it in other way and will put solution. – Gendarmerie

This solution is only correct if wsin a <= h (w being the longer side of the rotated rectangle), otherwise the rectangle with maximal area will not touch all sides; for wsin a > h two corners will lie on the mid-line between the two longer sides. see Jeffreys correct solution: #5789739 or my own answer to an equivalent question: #16703466 – Bignonia

Cramer is NEVER a good way to solve a linear system of equations. That it is taught as such in text books is a tragedy, but this is something one should not encourage for novices. – Boydboyden

Answer 3

First, we take care of the trivial case where the angle is zero or a multiple of pi/2. Then the largest rectangle is the same as the original rectangle.

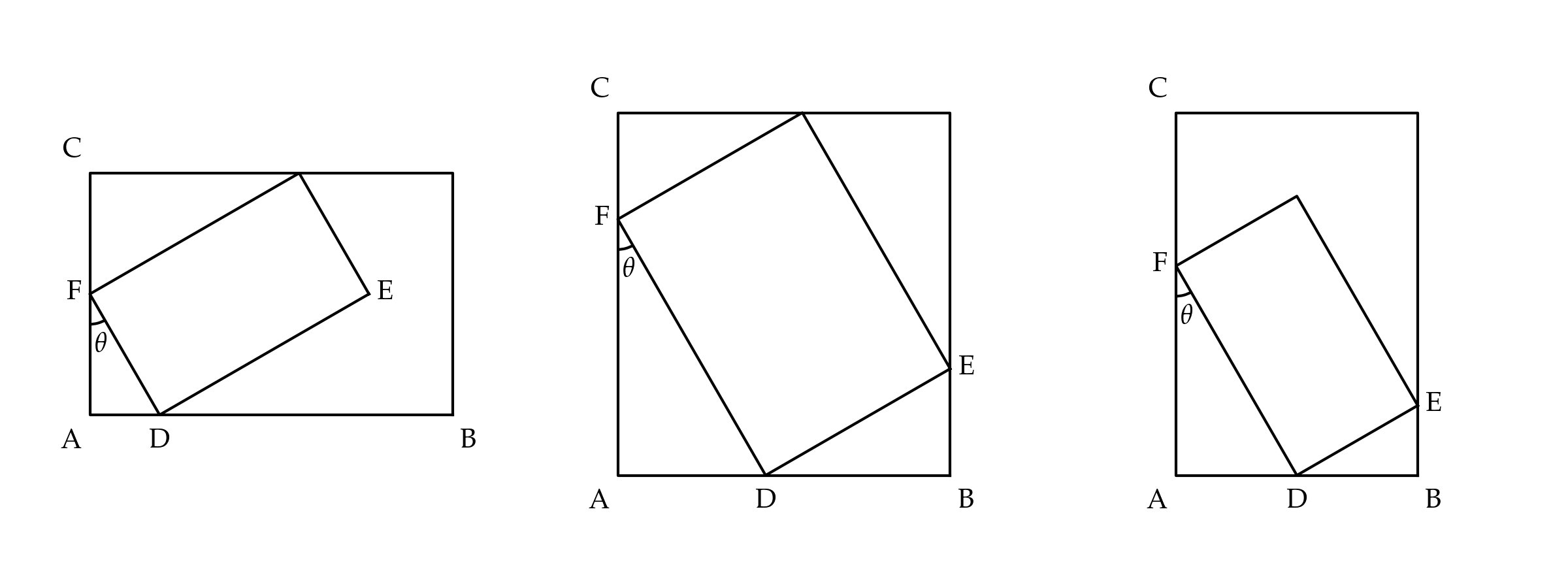
In general, the inner rectangle will have 3 points on the boundaries of the outer rectangle. If it does not, then it can be moved so that one vertex will be on the bottom, and one vertex will be on the left. You can then enlarge the inner rectangle until one of the two remaining vertices hits a boundary.

We call the sides of the outer rectangle R1 and R2. Without loss of generality, we can assume that R1 <= R2. If we call the sides of the inner rectangle H and W, then we have that

H cos a + W sin a <= R1
H sin a + W cos a <= R2

Since we have at least 3 points on the boundaries, at least one of these inequality must actually be an equality. Let's use the first one. It is easy to see that:

W = (R1 - H cos a) / sin a

and so the area is

A = H W = H (R1 - H cos a) / sin a

We can take the derivative wrt. H and require it to equal 0:

dA/dH = ((R1 - H cos a) - H cos a) / sin a

Solving for H and using the expression for W above, we find that:

H = R1 / (2 cos a)
W = R1 / (2 sin a)

Substituting this in the second inequality becomes, after some manipulation,

R1 (tan a + 1/tan a) / 2 <= R2

The factor on the left-hand side is always at least 1. If the inequality is satisfied, then we have the solution. If it isn't satisfied, then the solution is the one that satisfies both inequalities as equalities. In other words: it is the rectangle which touches all four sides of the outer rectangle. This is a linear system with 2 unknowns which is readily solved:

H = (R2 cos a - R1 sin a) / cos 2a
W = (R1 cos a - R2 sin a) / cos 2a

In terms of the original coordinates, we get:

x1 = x4 = W sin a cos a
y1 = y2 = R2 sin a - W sin^2 a 
x2 = x3 = x1 + H
y3 = y4 = y2 + W

Red

I'll try to find some time to check your solution. Can you see a quick way to get the xy position (one will do if there are multiple positions) of the target inner rectangle? – Builder

Indeed this seems to be the only solution correctly distinguishing the two cases 1) R2 is long enough for getting the optimal solution in terms of R1 (and the optimal rectangle does not touch the fourth side) 2) the optimal rectangle touches all 4 sides. Case 1) has an interesting property: the rectangle with maximal area touches the outer rectangle in the mid-point of the shorter side. – Bignonia

I tried this solution (for my question posted here: #16703466), but was unable to reproduce your results - can you update your answer to include a complete pseudocode function listing? – Trixie

E.g. what do you mean by 'the outer rectangle'? Are R1 and R2 the dimensions of the original rectangle? Or the larger rectangle that bounds the rotated rectangle? – Trixie

@Trixie Look at the second image in the question. The outer rectangle is the red one. Also note the condition R1 <= R2. If that is not the case, you have to make adjustments accordingly. – Red

I have given an implementation equivalent to this solution here: #16703466 . To avoid singularities I have, for instance, reformulated the condition for case distinction using tan a + 1/tan a = 1/(sin a cos a) and bringing the denominator to the other side. – Bignonia

@JeffreySax congratulations by this answer... I've tested it against a brute force optimization algorithm and it has given the same results so far... – Stores

This is correct and complete. It should be the accepted answer. – Paramagnet

Answer 4

Edit: My Mathematica answer below is wrong - I was solving a slightly different problem than what I think you are really asking.

To solve the problem you are really asking, I would use the following algorithm(s):

On the Maximum Empty Rectangle Problem

Using this algorithm, denote a finite amount of points that form the boundary of the rotated rectangle (perhaps a 100 or so, and make sure to include the corners) - these would be the set S decribed in the paper.

.

.

.

.

.

For posterity's sake I have left my original post below:

The inside rectangle with the largest area will always be the rectangle where the lower mid corner of the rectangle (the corner near the alpha on your diagram) is equal to half of the width of the outer rectangle.

I kind of cheated and used Mathematica to solve the algebra for me:

From this you can see that the maximum area of the inner rectangle is equal to 1/4 width^2 * cosecant of the angle times the secant of the angle.

Now I need to figure out what is the x value of the bottom corner for this optimal condition. Using the Solve function in mathematica on my area formula, I get the following:

Which shows that the x coordinate of the bottom corner equals half of the width.

Now just to make sure, I'll going to test our answer empirically. With the results below you can see that indeed the highest area of all of my tests (definately not exhaustive but you get the point) is when the bottom corner's x value = half of the outer rectangle's width.

Jacklight

i've never used Mathematica. Could you expand some more so I can understand whats happening? – Builder

Jason, please consider participating in the mathematica tag. – Examine

@belisarius sure, why not? :-) – Examine

@Jason Moore Can you post the code (not just the image of the code) please – Chesnut

Answer 5

@Andri is not working correctly for image where width > height as I tested. So, I fixed and optimized his code by such way (with only two trigonometric functions):

calculateLargestRect = function(angle, origWidth, origHeight) {
    var w0, h0;
    if (origWidth <= origHeight) {
        w0 = origWidth;
        h0 = origHeight;
    }
    else {
        w0 = origHeight;
        h0 = origWidth;
    }
    // Angle normalization in range [-PI..PI)
    var ang = angle - Math.floor((angle + Math.PI) / (2*Math.PI)) * 2*Math.PI; 
    ang = Math.abs(ang);      
    if (ang > Math.PI / 2)
        ang = Math.PI - ang;
    var sina = Math.sin(ang);
    var cosa = Math.cos(ang);
    var sinAcosA = sina * cosa;
    var w1 = w0 * cosa + h0 * sina;
    var h1 = w0 * sina + h0 * cosa;
    var c = h0 * sinAcosA / (2 * h0 * sinAcosA + w0);
    var x = w1 * c;
    var y = h1 * c;
    var w, h;
    if (origWidth <= origHeight) {
        w = w1 - 2 * x;
        h = h1 - 2 * y;
    }
    else {
        w = h1 - 2 * y;
        h = w1 - 2 * x;
    }
    return {
        w: w,
        h: h
    }
}

UPDATE

Also I decided to post the following function for proportional rectange calculating:

calculateLargestProportionalRect = function(angle, origWidth, origHeight) {
    var w0, h0;
    if (origWidth <= origHeight) {
        w0 = origWidth;
        h0 = origHeight;
    }
    else {
        w0 = origHeight;
        h0 = origWidth;
    }
    // Angle normalization in range [-PI..PI)
    var ang = angle - Math.floor((angle + Math.PI) / (2*Math.PI)) * 2*Math.PI; 
    ang = Math.abs(ang);      
    if (ang > Math.PI / 2)
        ang = Math.PI - ang;
    var c = w0 / (h0 * Math.sin(ang) + w0 * Math.cos(ang));
    var w, h;
    if (origWidth <= origHeight) {
        w = w0 * c;
        h = h0 * c;
    }
    else {
        w = h0 * c;
        h = w0 * c;
    }
    return {
        w: w,
        h: h
    }
}

Horizon

Thanks for the fix. My answer was edited by Magnus Hoff at some point and I have not tested the new version. I know the old (ugly) version works, since I have been using it without problems for ~2 years now. – Pastille

Could this approach be used to calculate the bounding box of a rotated rectangle with some tweaking? In my project I need to simultaneously calculate largest rect within and bbox while I rotate a rectangle, it would be great if this could return both! – Imprison

Does not work properly for rectangles (not equal width and height) :( – Horizon

fixed and cleaned up... the solution wasn't at all obvious and i wouldn't have got there without your implementation, so thanks! – Imprison

Answer 6

Coproc solved this problem on another thread (https://stackoverflow.com/a/16778797) in a simple and efficient way. Also, he gave a very good explanation and python code there.

Below there is my Matlab implementation of his solution:

function [ CI, T ] = rotateAndCrop( I, ang )
%ROTATEANDCROP Rotate an image 'I' by 'ang' degrees, and crop its biggest
% inner rectangle.

[h,w,~] = size(I);
ang = deg2rad(ang);

% Affine rotation
R = [cos(ang) -sin(ang) 0; sin(ang) cos(ang) 0; 0 0 1];
T = affine2d(R);
B = imwarp(I,T);

% Largest rectangle
% solution from https://stackoverflow.com/a/16778797

wb = w >= h;
sl = w*wb + h*~wb;
ss = h*wb + w*~wb;

cosa = abs(cos(ang));
sina = abs(sin(ang));

if ss <= 2*sina*cosa*sl
    x = .5*min([w h]);
    wh = wb*[x/sina x/cosa] + ~wb*[x/cosa x/sina];
else
    cos2a = (cosa^2) - (sina^2);
    wh = [(w*cosa - h*sina)/cos2a (h*cosa - w*sina)/cos2a]; 
end

hw = flip(wh);

% Top-left corner
tl = round(max(size(B)/2 - hw/2,1));

% Bottom-right corner
br = tl + round(hw);

% Cropped image
CI = B(tl(1):br(1),tl(2):br(2),:);

Chippy

Answer 7

sorry for not giving a derivation here, but I solved this problem in Mathematica a few days ago and came up with the following procedure, which non-Mathematica folks should be able to read. If in doubt, please consult http://reference.wolfram.com/mathematica/guide/Mathematica.html

The procedure below returns the width and height for a rectangle with maximum area that fits into another rectangle of width w and height h that has been rotated by alpha.

CropRotatedDimensionsForMaxArea[{w_, h_}, alpha_] := 
With[
  {phi = Abs@Mod[alpha, Pi, -Pi/2]},
  Which[
   w == h, {w,h} Csc[phi + Pi/4]/Sqrt[2],
   w > h, 
     If[ Cos[2 phi]^2 < 1 - (h/w)^2, 
       h/2 {Csc[phi], Sec[phi]}, 
       Sec[2 phi] {w Cos[phi] - h Sin[phi], h Cos[phi] - w Sin[phi]}],
   w < h, 
     If[ Cos[2 phi]^2 < 1 - (w/h)^2, 
       w/2 {Sec[phi], Csc[phi]}, 
       Sec[2 phi] {w Cos[phi] - h Sin[phi], h Cos[phi] - w Sin[phi]}]
  ]
]

Ephraimite

What is Abs@Mod and Csc and Sec? – Ara

Answer 8

Here is the easiest way to do this... :)

Step 1
//Before Rotation

int originalWidth = 640;
int originalHeight = 480;

Step 2
//After Rotation
int newWidth = 701;  //int newWidth = 654;  //int newWidth = 513;
int newHeight = 564; //int newHeight = 757; //int newHeight = 664;

Step 3
//Difference in height and width
int widthDiff ;
int heightDiff;
int ASPECT_RATIO = originalWidth/originalHeight; //Double check the Aspect Ratio

if (newHeight > newWidth) {

    int ratioDiff = newHeight - newWidth;
    if (newWidth < Constant.camWidth) {
        widthDiff = (int) Math.floor(newWidth / ASPECT_RATIO);
        heightDiff = (int) Math.floor((originalHeight - (newHeight - originalHeight)) / ASPECT_RATIO);
    }
    else {
        widthDiff = (int) Math.floor((originalWidth - (newWidth - originalWidth) - ratioDiff) / ASPECT_RATIO);
        heightDiff = originalHeight - (newHeight - originalHeight);
    }

} else {
    widthDiff = originalWidth - (originalWidth);
    heightDiff = originalHeight - (newHeight - originalHeight);
}

Step 4
//Calculation
int targetRectanleWidth = originalWidth - widthDiff;
int targetRectanleHeight = originalHeight - heightDiff;

Step 5
int centerPointX = newWidth/2;
int centerPointY = newHeight/2;

Step 6
int x1 = centerPointX - (targetRectanleWidth / 2); 
int y1 = centerPointY - (targetRectanleHeight / 2);
int x2 = centerPointX + (targetRectanleWidth / 2);
int y2 = centerPointY + (targetRectanleHeight / 2);

Step 7
x1 = (x1 < 0 ? 0 : x1);
y1 = (y1 < 0 ? 0 : y1);

Melaniemelanin

widthDiff = originalWidth - (originalWidth); that will be always 0 – Ara

Answer 9

This is just an illustration of Jeffrey Sax's solution above, for my future reference.

With reference to the diagram above, the solution is:

(I used the identity tan(t) + cot(t) = 2/sin(2t))

Paramagnet

Counter-example: AB = AC = 10 θ = 45 deg cos(θ) = sin(θ) = 0.707... sin(2θ) = 1 cos(2θ) = 0 Therefore: (AB * cos(θ) - AC * sin(θ)) / cos(2θ) = 0 / 0 = undefined. Maybe the conditionals need to be ≤ instead of <? – Reifel

You are right. The third case formula is still correct in the limit: if you take theta = pi/4 + epsilon and take the limit epsilon -> 0, it will give the right answer. This means that the formula is probably numerically unstable in some region of parameter space, and replacing < with <= is unlikely to completely fix the issue. It may take some work to obtain a numerically stable formula. – Paramagnet