Puzzle: Find largest rectangle (maximal rectangle problem)

Question

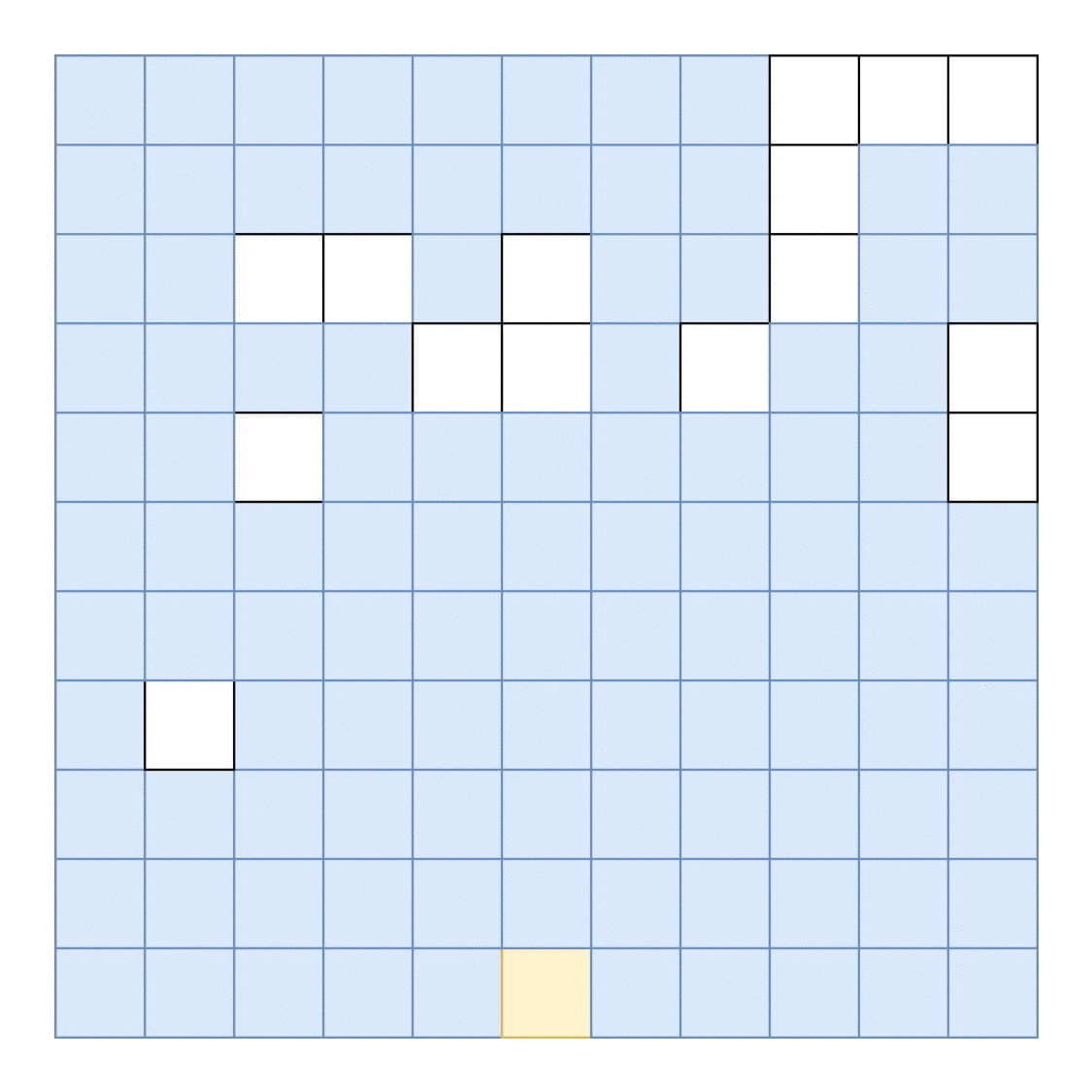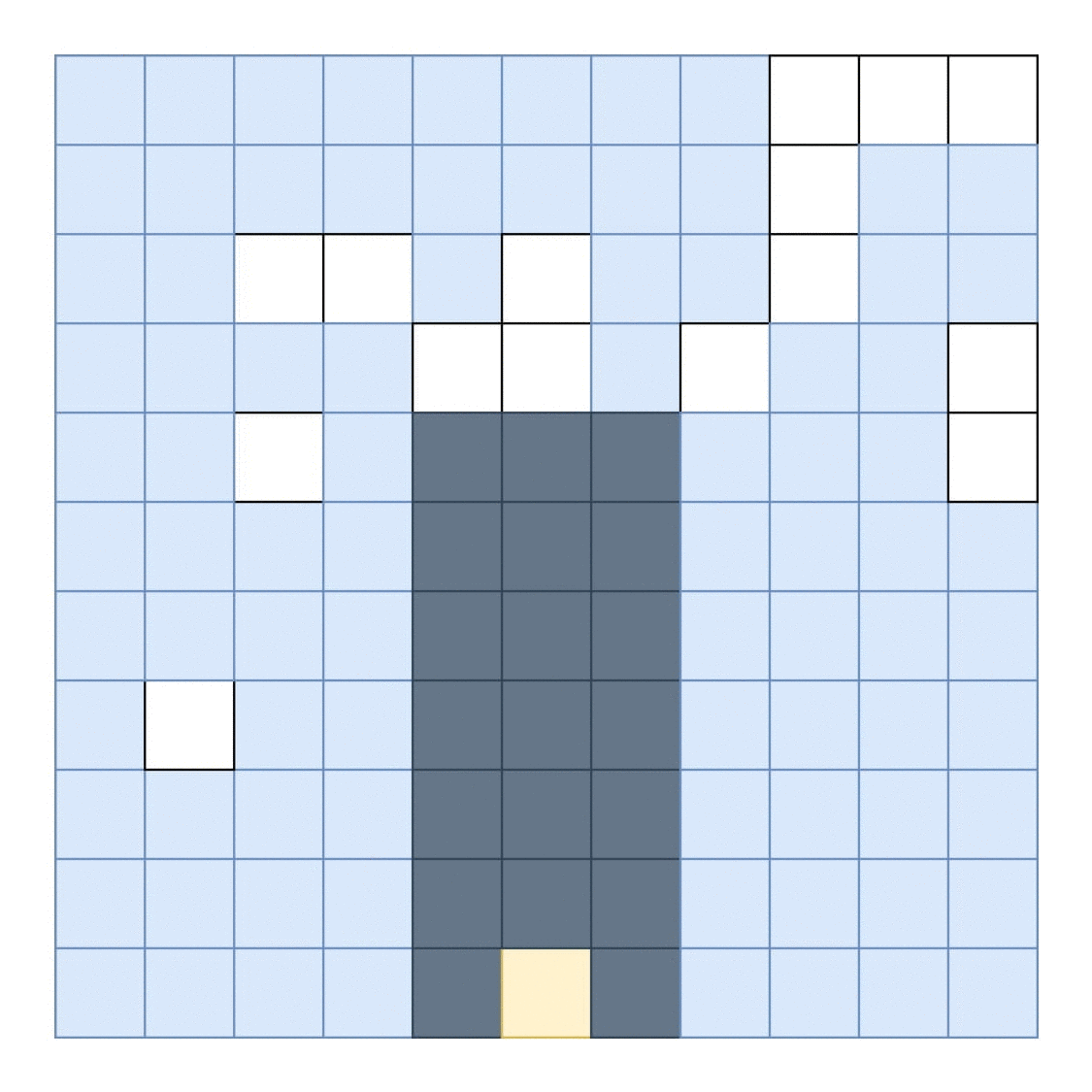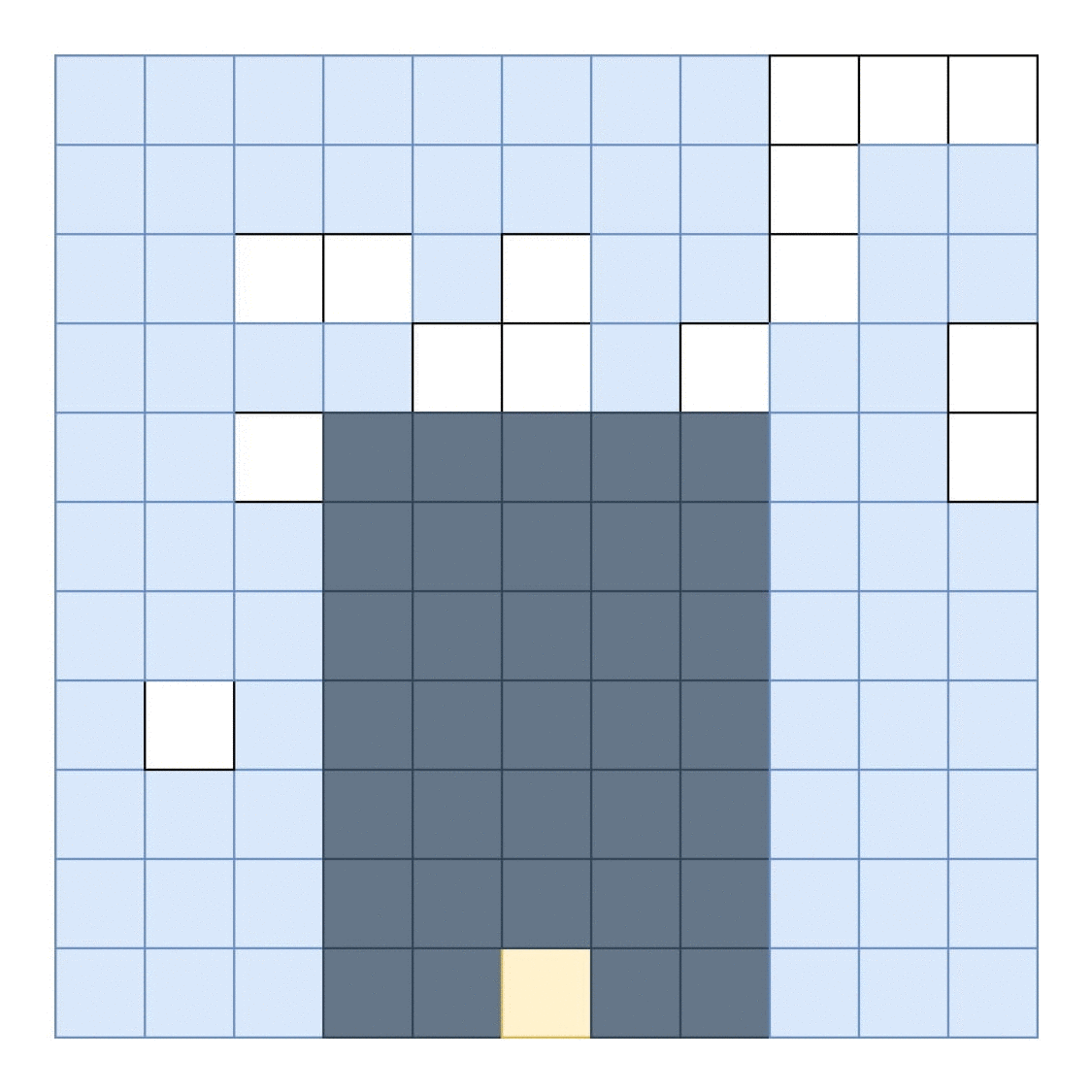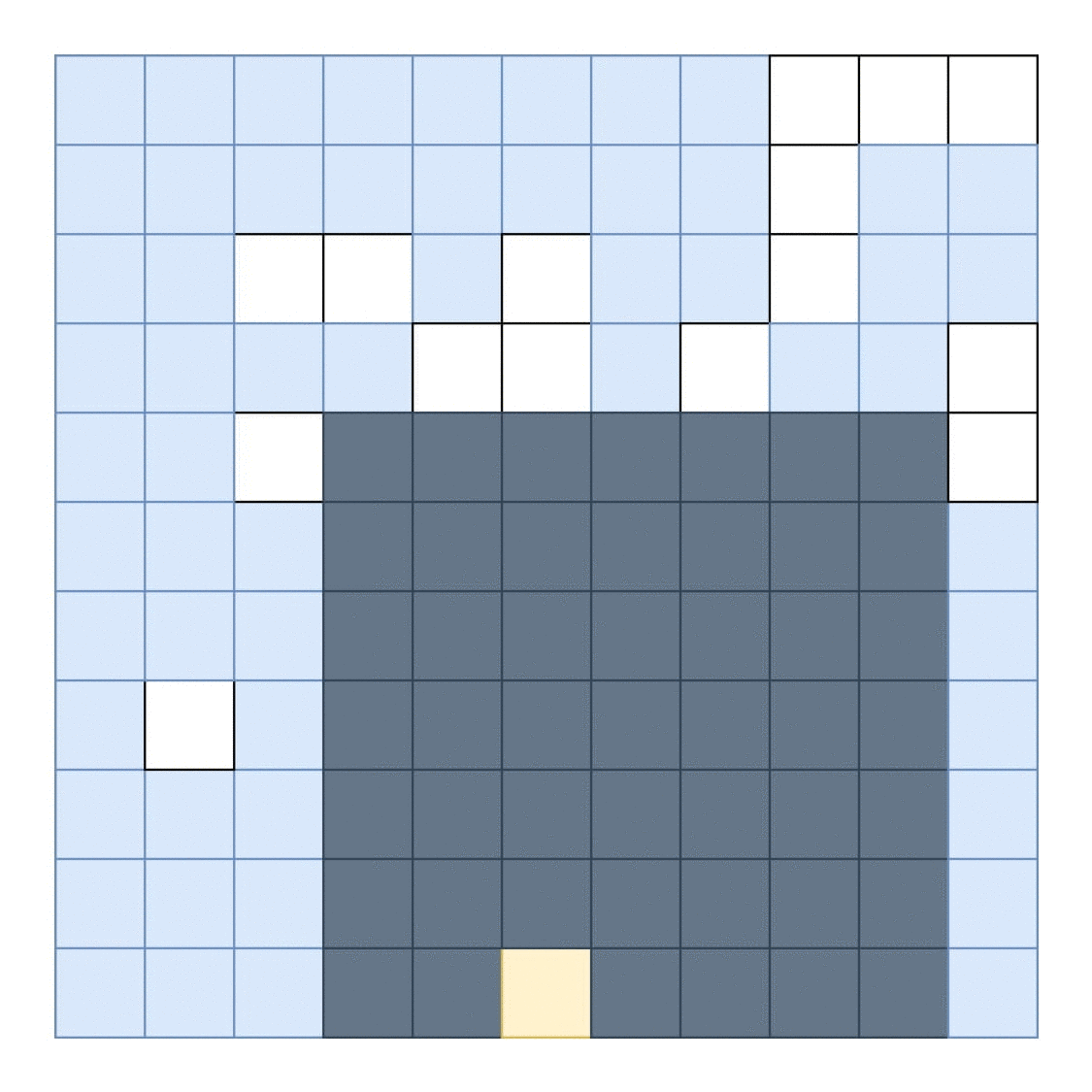
What's the most efficient algorithm to find the rectangle with the largest area which will fit in the empty space?

Let's say the screen looks like this ('#' represents filled area):

....................
..............######
##..................
.................###
.................###
#####...............
#####...............
#####...............

A probable solution is:

....................
..............######
##...++++++++++++...
.....++++++++++++###
.....++++++++++++###
#####++++++++++++...
#####++++++++++++...
#####++++++++++++...

Normally I'd enjoy figuring out a solution. Although this time I'd like to avoid wasting time fumbling around on my own since this has a practical use for a project I'm working on. Is there a well-known solution?

Shog9 wrote:

Is your input an array (as implied by the other responses), or a list of occlusions in the form of arbitrarily sized, positioned rectangles (as might be the case in a windowing system when dealing with window positions)?

Yes, I have a structure which keeps track of a set of windows placed on the screen. I also have a grid which keeps track of all the areas between each edge, whether they are empty or filled, and the pixel position of their left or top edge. I think there is some modified form which would take advantage of this property. Do you know of any?

Kyd

Answer 1

@lassevk

I found the referenced article, from DDJ: The Maximal Rectangle Problem

Kyd

This one is O(mn) time, which is optimal. – Huarache

Answer 2

I'm the author of that Dr. Dobb's article and get occasionally asked about an implementation. Here is a simple one in C:

#include <assert.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct {
  int one;
  int two;
} Pair;

Pair best_ll = { 0, 0 };
Pair best_ur = { -1, -1 };
int best_area = 0;

int *c; /* Cache */
Pair *s; /* Stack */
int top = 0; /* Top of stack */

void push(int a, int b) {
  s[top].one = a;
  s[top].two = b;
  ++top;
}

void pop(int *a, int *b) {
  --top;
  *a = s[top].one;
  *b = s[top].two;
}


int M, N; /* Dimension of input; M is length of a row. */

void update_cache() {
  int m;
  char b;
  for (m = 0; m!=M; ++m) {
    scanf(" %c", &b);
    fprintf(stderr, " %c", b);
    if (b=='0') {
      c[m] = 0;
    } else { ++c[m]; }
  }
  fprintf(stderr, "\n");
}


int main() {
  int m, n;
  scanf("%d %d", &M, &N);
  fprintf(stderr, "Reading %dx%d array (1 row == %d elements)\n", M, N, M);
  c = (int*)malloc((M+1)*sizeof(int));
  s = (Pair*)malloc((M+1)*sizeof(Pair));
  for (m = 0; m!=M+1; ++m) { c[m] = s[m].one = s[m].two = 0; }
  /* Main algorithm: */
  for (n = 0; n!=N; ++n) {
    int open_width = 0;
    update_cache();
    for (m = 0; m!=M+1; ++m) {
      if (c[m]>open_width) { /* Open new rectangle? */
        push(m, open_width);
        open_width = c[m];
      } else /* "else" optional here */
      if (c[m]<open_width) { /* Close rectangle(s)? */
        int m0, w0, area;
        do {
          pop(&m0, &w0);
          area = open_width*(m-m0);
          if (area>best_area) {
            best_area = area;
            best_ll.one = m0; best_ll.two = n;
            best_ur.one = m-1; best_ur.two = n-open_width+1;
          }
          open_width = w0;
        } while (c[m]<open_width);
        open_width = c[m];
        if (open_width!=0) {
          push(m0, w0);
        }
      }
    }
  }
  fprintf(stderr, "The maximal rectangle has area %d.\n", best_area);
  fprintf(stderr, "Location: [col=%d, row=%d] to [col=%d, row=%d]\n",
                  best_ll.one+1, best_ll.two+1, best_ur.one+1, best_ur.two+1);
  return 0;
}

It takes its input from the console. You could e.g. pipe this file to it:

16 12
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 1 1 0 0 1 0 0 0 1 1 0 1 0
0 0 0 1 1 0 1 1 1 0 1 1 1 0 1 0
0 0 0 0 1 1 * * * * * * 0 0 1 0
0 0 0 0 0 0 * * * * * * 0 0 1 0
0 0 0 0 0 0 1 1 0 1 1 1 1 1 1 0
0 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 
0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0

And after printing its input, it will output:

The maximal rectangle has area 12.
Location: [col=7, row=6] to [col=12, row=5]

The implementation above is nothing fancy of course, but it's very close to the explanation in the Dr. Dobb's article and should be easy to translate to whatever is needed.

Irrespirable

Do you have a copy of that Dr. Dobbs article (or something similar) online somewhere? The original at drdobbs.com/database/the-maximal-rectangle-problem/… seems to have died, unfortunately. If you reply, I'll update my answer here too. Thanks! – Huarache

Oh, that's really unfortunate :-( This must have happened fairly recently. I do have an archive of that web-page, but due to Dr. Dobb's copyright on it, I do not think I have the right to publish it. – Irrespirable

@Daveed V. - there is an Archive.org copy here web.archive.org/web/20150921112543/http://www.drdobbs.com/… – Actuary

Answer 3

I am the author of the Maximal Rectangle Solution on LeetCode, which is what this answer is based on.

Since the stack-based solution has already been discussed in the other answers, I would like to present an optimal O(NM) dynamic programming solution which originates from user morrischen2008.

Intuition

Imagine an algorithm where for each point we computed a rectangle by doing the following:

• Finding the maximum height of the rectangle by iterating upwards until a filled area is reached

• Finding the maximum width of the rectangle by iterating outwards left and right until a height that doesn't accommodate the maximum height of the rectangle

For example finding the rectangle defined by the yellow point:

We know that the maximal rectangle must be one of the rectangles constructed in this manner (the max rectangle must have a point on its base where the next filled square is height above that point).

For each point we define some variables:

h - the height of the rectangle defined by that point

l - the left bound of the rectangle defined by that point

r - the right bound of the rectangle defined by that point

These three variables uniquely define the rectangle at that point. We can compute the area of this rectangle with h * (r - l). The global maximum of all these areas is our result.

Using dynamic programming, we can use the h, l, and r of each point in the previous row to compute the h, l, and r for every point in the next row in linear time.

Algorithm

Given row matrix[i], we keep track of the h, l, and r of each point in the row by defining three arrays - height, left, and right.

height[j] will correspond to the height of matrix[i][j], and so on and so forth with the other arrays.

The question now becomes how to update each array.

height

h is defined as the number of continuous unfilled spaces in a line from our point. We increment if there is a new space, and set it to zero if the space is filled (we are using '1' to indicate an empty space and '0' as a filled one).

new_height[j] = old_height[j] + 1 if row[j] == '1' else 0

left:

Consider what causes changes to the left bound of our rectangle. Since all instances of filled spaces occurring in the row above the current one have already been factored into the current version of left, the only thing that affects our left is if we encounter a filled space in our current row.

As a result we can define:

new_left[j] = max(old_left[j], cur_left)

cur_left is one greater than rightmost filled space we have encountered. When we "expand" the rectangle to the left, we know it can't expand past that point, otherwise it'll run into the filled space.

right:

Here we can reuse our reasoning in left and define:

new_right[j] = min(old_right[j], cur_right)

cur_right is the leftmost occurrence of a filled space we have encountered.

Implementation

def maximalRectangle(matrix):
    if not matrix: return 0

    m = len(matrix)
    n = len(matrix[0])

    left = [0] * n # initialize left as the leftmost boundary possible
    right = [n] * n # initialize right as the rightmost boundary possible
    height = [0] * n

    maxarea = 0

    for i in range(m):

        cur_left, cur_right = 0, n
        # update height
        for j in range(n):
            if matrix[i][j] == '1': height[j] += 1
            else: height[j] = 0
        # update left
        for j in range(n):
            if matrix[i][j] == '1': left[j] = max(left[j], cur_left)
            else:
                left[j] = 0
                cur_left = j + 1
        # update right
        for j in range(n-1, -1, -1):
            if matrix[i][j] == '1': right[j] = min(right[j], cur_right)
            else:
                right[j] = n
                cur_right = j
        # update the area
        for j in range(n):
            maxarea = max(maxarea, height[j] * (right[j] - left[j]))

    return maxarea

Avowed

Answer 4

I implemented the solution of Dobbs in Java.

No warranty for anything.

package com.test;

import java.util.Stack;

public class Test {

    public static void main(String[] args) {
        boolean[][] test2 = new boolean[][] { new boolean[] { false, true, true, false },
                new boolean[] { false, true, true, false }, new boolean[] { false, true, true, false },
                new boolean[] { false, true, false, false } };
        solution(test2);
    }

    private static class Point {
        public Point(int x, int y) {
            this.x = x;
            this.y = y;
        }

        public int x;
        public int y;
    }

    public static int[] updateCache(int[] cache, boolean[] matrixRow, int MaxX) {
        for (int m = 0; m < MaxX; m++) {
            if (!matrixRow[m]) {
                cache[m] = 0;
            } else {
                cache[m]++;
            }
        }
        return cache;
    }

    public static void solution(boolean[][] matrix) {
        Point best_ll = new Point(0, 0);
        Point best_ur = new Point(-1, -1);
        int best_area = 0;

        final int MaxX = matrix[0].length;
        final int MaxY = matrix.length;

        Stack<Point> stack = new Stack<Point>();
        int[] cache = new int[MaxX + 1];

        for (int m = 0; m != MaxX + 1; m++) {
            cache[m] = 0;
        }

        for (int n = 0; n != MaxY; n++) {
            int openWidth = 0;
            cache = updateCache(cache, matrix[n], MaxX);
            for (int m = 0; m != MaxX + 1; m++) {
                if (cache[m] > openWidth) {
                    stack.push(new Point(m, openWidth));
                    openWidth = cache[m];
                } else if (cache[m] < openWidth) {
                    int area;
                    Point p;
                    do {
                        p = stack.pop();
                        area = openWidth * (m - p.x);
                        if (area > best_area) {
                            best_area = area;
                            best_ll.x = p.x;
                            best_ll.y = n;
                            best_ur.x = m - 1;
                            best_ur.y = n - openWidth + 1;
                        }
                        openWidth = p.y;
                    } while (cache[m] < openWidth);
                    openWidth = cache[m];
                    if (openWidth != 0) {
                        stack.push(p);
                    }
                }
            }
        }

        System.out.printf("The maximal rectangle has area %d.\n", best_area);
        System.out.printf("Location: [col=%d, row=%d] to [col=%d, row=%d]\n", best_ll.x + 1, best_ll.y + 1,
                best_ur.x + 1, best_ur.y + 1);
    }

}

Drenthe

Answer 5

@lassevk

    // 4. Outer double-for-loop to consider all possible positions 
    //    for topleft corner. 
    for (int i=0; i < M; i++) {
      for (int j=0; j < N; j++) {

        // 2.1 With (i,j) as topleft, consider all possible bottom-right corners. 

        for (int a=i; a < M; a++) {
          for (int b=j; b < N; b++) {

HAHA... O(m2 n2).. That's probably what I would have come up with.

I see they go on to develop optmizations... looks good, I'll have a read.

Kyd

Answer 6

Implementation of the stack-based algorithm in plain Javascript (with linear time complexity):

function maxRectangle(mask) {
  var best = {area: 0}
  const width = mask[0].length
  const depth = Array(width).fill(0)
  for (var y = 0; y < mask.length; y++) {
    const ranges = Array()
    for (var x = 0; x < width; x++) {
      const d = depth[x] = mask[y][x] ? depth[x] + 1 : 0
      if (!ranges.length || ranges[ranges.length - 1].height < d) {
        ranges.push({left: x, height: d})
      } else {
        for (var j = ranges.length - 1; j >= 0 && ranges[j].height >= d; j--) {
          const {left, height} = ranges[j]
          const area = (x - left) * height
          if (area > best.area) {
            best = {area, left, top: y + 1 - height, right: x, bottom: y + 1}
          }
        }
        ranges.splice(j+2)
        ranges[j+1].height = d
      }
    }
  }
  return best;
}

var example = [
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0],
[0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0],
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0],
[0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]]

console.log(maxRectangle(example))

Extemporize

had to change x < width to x <= width or last column would be skipped – Delcine