One analogy that I find useful in demystifying Prolog is that Backtracking is like Nested Loops, and when the innermost loop's variables' values are all found, the looping is suspended, the vars' values are reported, and then the looping is resumed.
As an example, let's write down simple generate-and-test program to find all pairs of natural numbers above 0 that sum up to a prime number. Let's assume is_prime/1 is already given to us.
We write this in Prolog as
above(0, N), between(1, N, M), Sum is M+N, is_prime(Sum).
We write this in an imperative pseudocode as
for N from 1 step 1:
for M from 1 step 1 until N:
Sum := M+N
if is_prime(Sum):
report_to_user_and_ask(Sum)
Now when report_to_user_and_ask is called, it prints Sum out and asks the user whether to abort or to continue. The loops are not exited, on the contrary, they are just suspended. Thus all the loop variables values that got us this far -- and there may be more tests up the loops chain that sometimes succeed and sometimes fail -- are preserved, i.e. the computation state is preserved, and the computation is ready to be resumed from that point, if the user presses ;.
This is what's known as "inversion of control" as far as I understand, with report_to_user_and_ask() being used as a callback.
I first saw this approach in Peter Norvig's AI book's implementation of Prolog in Common Lisp. He used mapping (Common Lisp's mapcan which is concatMap in Haskell or flatMap in many other languages) as a looping construct though, and it took me years to see that nested loops is what it is really all about.
Goals conjunction is expressed as the nesting of the loops (akin to multiplication); goals disjunction is expressed as the alternatives to loop through (akin to summation):
[ [a b] X [c d e] ] -- 2D
[ a : c d e
b : c d e ] -- 2*3 = 6
[ [a b] + [c d e] ] -- 1D
[ a b c d e ] -- 2+3 = 5
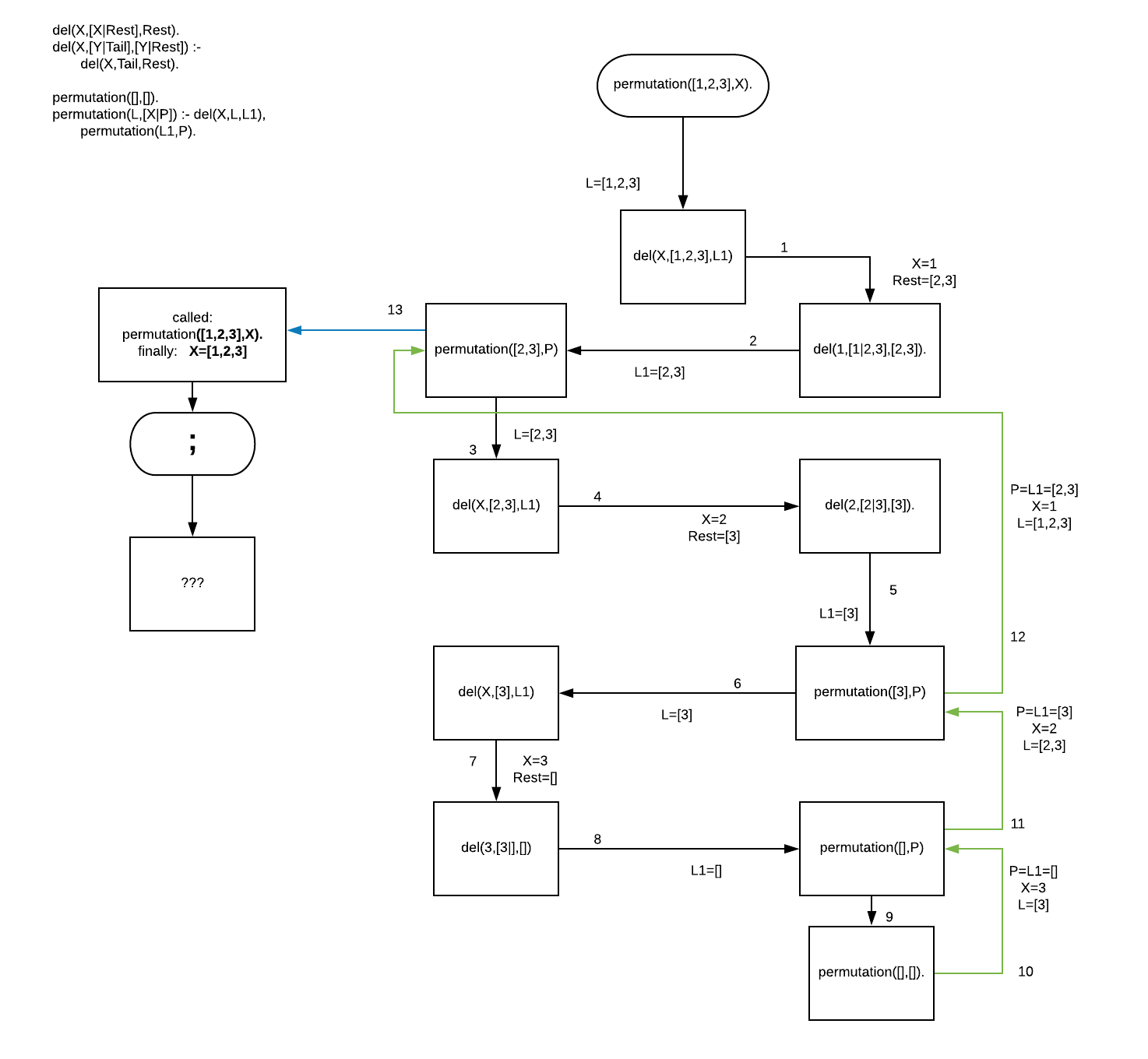
Further twist is that the nested loops' structure isn't fixed from the outset. It is fluid, the nested loops of a given loop can be created depending on the current state of that loop, i.e. depending on the current alternative being explored there; the loops are written as we go. In (most of the) languages where such dynamic creation of nested loops is impossible, it can be encoded with nested recursion / function invocation / inside the loops. (Here's one example, with some pseudocode.)
If we keep all such loops (created for each of the alternatives) in memory even after they are finished with, what we get is the AND-OR tree (mentioned in the other answer) thus being created while the search space is being explored and the solutions are found.
(non-coincidentally this fluidity is also the essence of "monad"; nondeterminism is modeled by the list monad; and the essential operation of the list monad is the flatMap operation which we saw above. With fluid structure of loops it is "Monad"; with fixed structure it is "Applicative Functor"; simple loops with no structure (no nesting at all): simply "Functor" (the concepts used in Haskell and the like). Also helps to demystify those.)
So, the proper slogan could be Backtracking is like Nested Loops, either fixed, known from the outset, or dynamically-created as we go. It's a bit longer though. :)
Here's also a Prolog example, which "as if creates the code to be run first (N nested loops for a given value of N), and then runs it." (There's even a whole dedicated tag for it on SO, too, it turns out, recursive-backtracking.)
And here's one in Scheme ("creates nested loops with the solution being accessible in the innermost loop's body"), and a C++ example ("create n nested loops at run-time, in effect enumerating the binary encoding of 2n, and print the sums out from the innermost loop").