Divide an image by grouping similar pixels into rectangles

Question

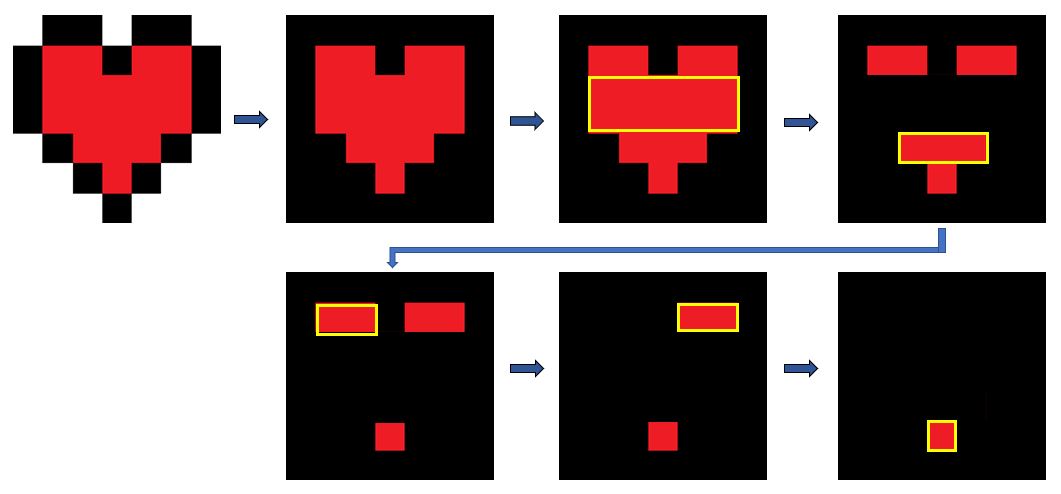
consider an image like this:

by grouping pixels by color into distinct rectangles, different configurations might be achieved, for example:

the goal is to find one of the best configurations, i.e. a configuration which has the least possible number of rectangles (rectangles sizes are not important).

any idea on how to design an efficient algorithm which is able to solve this problem?

EDIT: i think the best answer is the one by @dshin, as they proved that this problem is a NP-HARD one so there probably isn't any efficient solution that is able to guarantee an optimal result. other answers provide reasonable compromises to get an acceptable solution, but that won't always be the optimal one.

Overfeed

Welcome to SO! What have you tried so far? Please share them. Also did you get any ideas from #5919798 ? – Dovekie

@JeruLuke hello and thank you! for the moment i'm using a "row-based" approach, that is using rectangles Nx1 size, that's simple to implement but not always optimized in terms of number of rectangles... – Overfeed

question looks familiar. did you delete the last one? it was closed for being a duplicate, IIRC -- this could be an "NP" problem. it requires approximative algorithms if you have a big problem and still want to get done soon. this computer science or math/geometry. programming is not the problem here. you should try asking on other stackexchanges like cs.stackexchange.com or math.stackexchange.com – Ringent

@ChristophRackwitz sorry it's my first time on SO, did i really post a wrong question? i see many questions like this here (i can see them also in the "Related" section here), can you please tell me why you consider mine to be different (and wrong)? – Overfeed

I think it's okay. you got an interesting answer below that should help you reach a solution and that's the goal. I suggested other stack exchanges because the experts for your specific problem may not hang out around here. – Ringent

Answer 1

Each connected colored region is a rectilinear polygon that can be considered independently, and so your problem amounts to solving the minimum rectangle covering for rectilinear polygons. This is a well-studied problem that finds applications in some fields, like VLSI.

For convex rectilinear polygons, there is an algorithm that finds the optimal solution in polynomial time, described in this 1984 thesis.

The non-convex case is NP-hard (reference), so an efficient optimal solution likely does not exist. But there are several algorithms which produce good empirical results. This 1990 publication describes three separate algorithms, each of which are guaranteed to use at most twice as many rectangles as the optimal solution. This 2016 publication describes an algorithm that uses the common IP + LP relaxation technique, which apparently produces better results in real-life problem instances, although lacking in theoretical guarantees. Unfortunately, both publications are behind paywalls, and I haven't been able to find free resources that describe the algorithms.

If you are just looking for something reasonable, and your problem instances are not pathological in nature, then the algorithms described in other answers are probably good enough.

Oblivious

very interesting literature, i'm sure going to take a deep look into it, thanks! – Overfeed

Answer 2

I don't have a proof but my feeling is a greedy approach should solve this problem:

1. Start on the upper left (or in whichever corner)
2. Expand rectangle 1px to the right as long as colors match
3. Expand rectangle 1px to the bottom as long as all colors in that row match
4. Line by line and column by column, find the next pixel that is not already part of a square (maybe keep track of visited pixels in a second array) and repeat 2 and 3.

You can switch lines and columns and go up and left or whatever instead and end up with different configurations, but from playing this through in my mind I think the number of rectangles should always be the same.

Drambuie

The technical term would be floodfill. Your approach is iterative floodfilling based on color. Good thought! – Dovekie

I don’t believe this will always use the minimum number of rectangles. Consider a 2x100 grid where all cells are white except for the top-right, bottom-right, and the cell one spot to the left of the bottom right, which are red. The optimal approach uses four rectangles. Your approach will use many more than this. – Rodriquez

No it won't, I guess? I assume you mean a height of 2 and width of 100. First rectangle would be over all white in the top row, second one just the top-right-red, third one all white in the second row, fourth one the two red in the bottom right. – Drambuie

@Drambuie i tried thinking about floodfill, but then i understood it is not enough as it doesn't divide colors into optimal rectangles: following your bullet points, you can see there is a problem, if i expand the row to its maximum i might obtain a long Nx1 row when the optimal solution would have been having a NxM area with a shorther width but a longer height. take the example picture: if i divide the red part "row by row" i get 6 rectangles, compared to the 5 ones you can see in the "divided" example. – Overfeed

@DrohGabuh but with the third step in my approach you would extend the rectangle in the second red line 1px further down, giving a 2x5 rectangle and 5 rectangles in total. 2nd step is to make the 1xN rectangle as wide as possible but 3rd step expands the same rectangle to its maximum height as well. My approach is similar to but differs from flood fill. – Drambuie

@Drambuie yes its true, but if i take max row width and only then worrying about height, you might end up in a situation with a Nx1 row only because the last pixel of the next row its not the same color... a better solution would have been taking a row of N-1 x M and then worrying about that last pixel. – Overfeed

@DrohGabuh True, rectangles would tend to be long and skinny. However, the total rectangle count is still optimal. If you want more nice-looking rectangles, alternate between expanding 1px to the right and 1px to the bottom. If you can no longer do one of the expansions, repeat the other one to maximum size. This basically grows a square and only at the end deviates to a rectangle. – Drambuie

@Drambuie actually the intent is to reduce the number of rectangles, not to make them pretty. giving that ill experiment more on your idea in order to find a proof that the number of rectangles will still be optimal as you claim. thank you for your tip!! – Overfeed

Then take my answer :) In you example it does not matter if you first take 1 x N and then M-1 x N-1 or first M x N-1 and then 1 x 1 for the last pixel. Gives the same number of rectangles. (notation: height x width) (only saw your edit now. glad i could help!) – Drambuie

@Drambuie you said you have no proof too but just a "feeling"... i think there need to be proof to mark as an answer, but i'll try to find it and if i do i will sure mark it! (ofc the algorithm should work for every example, not just mine) – Overfeed

@DrohGabuh Or you could mark it as accepted until you find a counter example ;) – Drambuie

example of how this algorithm can be forced into suboptimality: triangle pointing NW with diagonal going NE-SW. algorithm will slice single-pixel rows off the top instead of taking the large square out the middle and then the same recursively. -- the problem is non-convex in general. it has local maxima. -- still a better answer than the second one, which merely says to "find largest rectangle" (that was the essence of the question), remove, and iterate – Ringent

i found another simple example making this not optimal: imagine a colored reversed "T" shape, by starting top-left this algorithm produces 3 rectangles, but the optimal solution would have been 2. – Overfeed

I don't fully get @ChristophRackwitz's example without an image but I agree that the reversed T shape indeed represents a counterexample. I think you could improve on this (e.g. stop extending downwards if not all of the pixels one column to the right are a different color) to catch the T-case but in the end I agree these are all approximate solutions :) – Drambuie

Answer 3

The idea here is based on the following links: Link 1 and Link 2.

In both the cases, the largest possible rectangle is computed within a given polygon/shape. Check both the above links for details.

We can extend the idea above to the problem at hand.

Steps:

1. Filter the image by color (say red)
2. Find the largest possible rectangle in the red region. After doing so mask it.
3. Repeat to find the next biggest rectangle until all the portions in red have been covered.
4. Repeat the above for every unique color.

Overview:

Dovekie

"Find the largest possible rectangle" isn't a library function. you ought to elaborate on that step because it's the only non-trivial one. – Ringent

@ChristophRackwitz I have provided links for that and didn't want to repeat the same. Here I just wanted to show how that idea can be used. – Dovekie

@JeruLuke that's an interesting idea, i'm going to try this one. i guess i have to find a good method to find the largest rectangle as the ones you linked seem to be far more complex than what's needed here (they consider also diagonal lines which are not present here) – Overfeed

@JeruLuke working on this i noticed that also this procedure doesn't always guarantee an optimal solution in terms of number of rectangles. suppose a red "T" shape, if the vertical part is bigger than the horizontal part, that will be considered the biggest rectangle, cutting in half the horizontal part... that means 3 rectangles will be generated, but the optimal solution would be 2 – Overfeed