Finding largest inscribed rectangle in polygon

Question

I have a bunch of images with labeled polygons marked in red (255,0,0):

I want to extract the bounding box but inside the polygon as shown with the blue rectangle:

OpenCV cv.boundingRect gives me the outer bounding box but how to extract the inner bounding box?

Quadriplegia

do you have raster data or vector data? -- "largest inscribed rectangle in convex polygon" -- there was a similar question some weeks/months ago which allowed rotation. the solution was some iterative method. -- a distance transform might work, if you have raster data. if you have vector data, there are probably simpler methods. depending on how wild the quads can be, maybe not much simpler. – Retrogradation

do you only have convex polygons or also concave polygons? Here's a way to try this, which isn't optimal and might even fail in some cases, but seems to be working "ok" for many users: https://mcmap.net/q/452444/-how-do-i-crop-to-largest-interior-bounding-box-in-opencv by now there are additional newer answers, maybe better ones. – Evaporation

I have RGB images and the polygons are convex. – Quadriplegia

I was also thinking about extracting the 4 most outer points and create a rectangle out of it – Quadriplegia

You could use the largestinteriorrectangle package – Obituary

see github.com/OpenStitching/lir – Donyadoodad

Answer 1

This inscribed rectangle problem is a bit more complex than outer rectangle. A related general case is polygon inside polygon - the polygon containment problem is described in this 1983 paper. This algorithm determines whether a polygon with n points can fit another polygon with m points with a complexity of O(n^3 m^3(n+m)log(n+m)) complexity.

The restricted case of "Largest Inscribed Rectangles in Geometric Convex Sets" can be done much faster. Have a look at this 2019 paper (DeepAI Link) They consider the problem of finding inscribed boxes and axis-aligned inscribed boxes of maximum volume, inside a compact and solid convex set.

Here is another older easier to understand algorithm for convex polygons with good visualizations.

Here is a MATLAB implementation. but the code lacks comments and is a bit difficult to understand.

Here is a python implementation but a bit dated.

Dowland

Answer 2

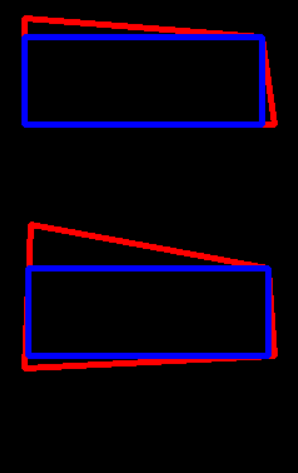
Suppose you have the two rectangles

import numpy as np

rect1 = np.array([[[20,15],[210,30],[220,100],[20,100]]], np.int32)
rect2 = np.array([[[25, 180], [215, 215], [220, 285], [20, 295]]], np.int32)

You can compute the largest inscribed polygon with the largestinteriorrectangle package. They come as [x, y, width, height].

import largestinteriorrectangle as lir

lir1 = lir.lir(rect1)  # array([20, 30, 191, 71])
lir2 = lir.lir(rect2)  # array([23, 215, 193, 71])

Let's plot this:

import cv2 as cv

img = np.zeros((380, 240, 3), dtype = "uint8")

cv.polylines(img, [rect1], True, (0,0,255), 3)
cv.polylines(img, [rect2], True, (0,0,255), 3)
    
cv.rectangle(img, lir.pt1(lir1), lir.pt2(lir1), (255,0,0), 3)
cv.rectangle(img, lir.pt1(lir2), lir.pt2(lir2), (255,0,0), 3)

cv.imshow('Shapes', img)
cv.waitKey(0)
cv.destroyAllWindows()

The package uses the algorithm of this paper

Note that the package uses numbas just in time compilation (JIT). So the very first time you import largestinteriorrectangle takes some time, but afterwards its blazingly fast

In your image, the blue rectangle don't touch the red polygon. So you would need to add 1 to x and y and substract 2 from width and height

Obituary

Answer 3

not a fast solution but this algorithm should give you the right biggest interior rectangle:

1. draw your contour as a mask with intensity values 1
2. compute the integral image of the mask https://en.wikipedia.org/wiki/Summed-area_table
3. for every pixel that has mask value > 0: for every pixel right/bottom to that pixel, test whether the whole rectangle is filled with white pixels, by reading 4 values from the integral image.

The integral image makes it more efficient than it should be, the algorithm itself is just brute-force.

int main()
{
    //std::vector<cv::Point> contour = { cv::Point(100,100), cv::Point(200,160), cv::Point(220, 230), cv::Point(90,270) };
    std::vector<cv::Point> contour = { cv::Point(100,100), cv::Point(150,200), cv::Point(200,160), cv::Point(220, 230), cv::Point(90,270) };
    //std::vector<cv::Point> contour = { cv::Point(100,100), cv::Point(200,100), cv::Point(200, 300), cv::Point(100,300) };

    cv::Mat img = cv::Mat::zeros(512, 512, CV_8UC3);
    cv::Mat mask = cv::Mat::zeros(img.size(), CV_8UC1);

    std::vector<std::vector<cv::Point> > contours = { contour };
    cv::drawContours(mask, contours, 0, cv::Scalar::all(1), -1); // mask values to 1 to make area == sum of pixels
    cv::drawContours(img, contours, 0, cv::Scalar(0, 0, 255), 1);

    cv::Mat integral;
    mask = mask;
    cv::integral(mask, integral, CV_32S);

    cv::Rect best;

    //cv::Mat legal = mask.clone();
    for (int y = 0; y < mask.rows; ++y)
    {
        std::cout << y << std::endl;
        for (int x = 0; x < mask.cols; ++x)
        {
            if (mask.at<uchar>(y, x) == 0) continue;
            cv::Point i1 = cv::Point(x, y);
            int val1 = integral.at<int>(i1);
            for (int y2 = y + 1; y2 < integral.rows; ++y2)
                for (int x2 = x + 1; x2 < integral.cols; ++x2)
                {
                    
                    cv::Point i2 = cv::Point(x2, y);
                    cv::Point i3 = cv::Point(x, y2);
                    cv::Point i4 = cv::Point(x2, y2);
                    if (mask.at<uchar>(i4) == 0) continue;
                    int val2 = integral.at<int>(i2);
                    int val3 = integral.at<int>(i3);
                    int val4 = integral.at<int>(i4);

                    int area = val1 + val4 - val2 - val3;
                    if (area != (x2 - x) * (y2 - y))
                    {
                        //std::cout << i1 << " to " << i4 << " = w:" << (x2 - x) << " h:" << (y2 - y) << std::endl;
                        //std::cout << area << " vs. " << (x2 - x) * (y2 - y) << std::endl;
                        //legal.at<uchar>(y, x) = 0;
                        //std::cin.get();
                    }
                    else
                    {
                        if (area > best.area()) best = cv::Rect(i1, i4);
                    }
                }
        }
        
    }

    cv::rectangle(img, best, cv::Scalar(255, 0, 0), 1);

    cv::imshow("img", img);
    cv::imshow("mask", mask>0);
    cv::waitKey(0);
}

Evaporation

Answer 4

Was trying lir for compute the interior rectangle but don't fit properly on wide of contour, I don't know why.
In the other hands Micka code do the job very well, but is to slow in violet is the original contour, and blue is the fitted rectangle.
Finally using lir create some black image and draw the contour inside

grid =np.zeros(binary_image.shape, dtype = "uint8")
cv2.fillPoly(grid, pts =[contoura], color=(255,255,255))<BR>

and get the result I was looking for (using lir)

Kevakevan