Let's have a look at the source code:
In the filter_update function pykalman checks, if the current observation is masked or not.
def filter_update(...)
# Make a masked observation if necessary
if observation is None:
n_dim_obs = observation_covariance.shape[0]
observation = np.ma.array(np.zeros(n_dim_obs))
observation.mask = True
else:
observation = np.ma.asarray(observation)
It does not impact the prediction step. But the correction step have two options. It happens in the _filter_correct function.
def _filter_correct(...)
if not np.any(np.ma.getmask(observation)):
# the normal Kalman Filter math
else:
n_dim_state = predicted_state_covariance.shape[0]
n_dim_obs = observation_matrix.shape[0]
kalman_gain = np.zeros((n_dim_state, n_dim_obs))
# !!!! the corrected state takes the result of the prediction !!!!
corrected_state_mean = predicted_state_mean
corrected_state_covariance = predicted_state_covariance
So as you can see this is exactly the theoretical approach.
Here is a short example and working data to play with.
Assume you have a gps receiver and you want to track yourself while walking. The receiver has a good accuracy. For simplification assume you go straight forward only.
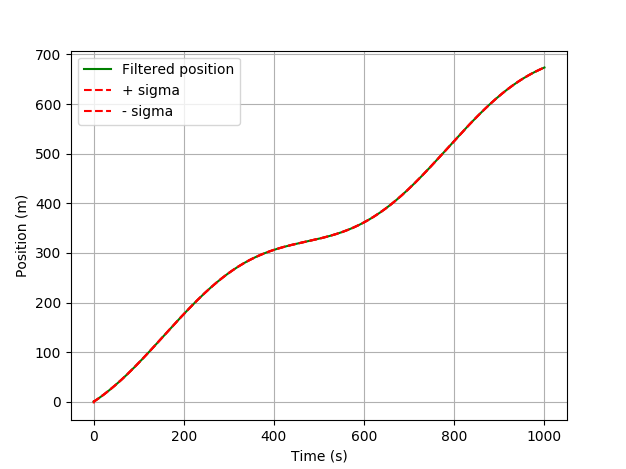
![pykalman estimation of the position using a gps receiver without masked observations]()
Nothing interesting happens. The filter estimates your position very well because of a good gps signal. What happens if you have no signal for a while?
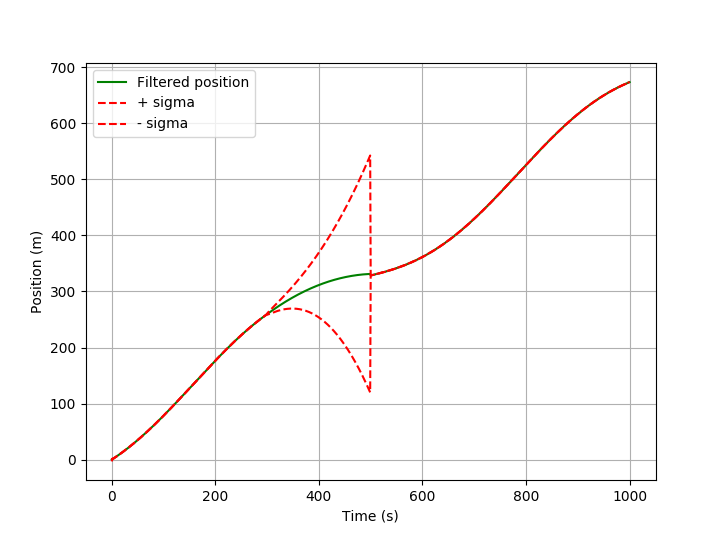
![pykalman estimation using masked observations]()
The filter can only predict based on the existing state and the knowledge about the system dynamics (see matrix Q). With each prediction step the uncertainty grows. The 1-Sigma range around the estimated position gets bigger. As soon as a new observation is there again, the state is corrected.
Here is the code and the data:
from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
from numpy import ma
# enable or disable missing observations
use_mask = 1
# reading data (quick and dirty)
Time=[]
X=[]
for line in open('data/dataset_01.csv'):
f1, f2 = line.split(';')
Time.append(float(f1))
X.append(float(f2))
if (use_mask):
X = ma.asarray(X)
X[300:500] = ma.masked
# Filter Configuration
# time step
dt = Time[2] - Time[1]
# transition_matrix
F = [[1, dt, 0.5*dt*dt],
[0, 1, dt],
[0, 0, 1]]
# observation_matrix
H = [1, 0, 0]
# transition_covariance
Q = [[ 1, 0, 0],
[ 0, 1e-4, 0],
[ 0, 0, 1e-6]]
# observation_covariance
R = [0.04] # max error = 0.6m
# initial_state_mean
X0 = [0,
0,
0]
# initial_state_covariance
P0 = [[ 10, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]
n_timesteps = len(Time)
n_dim_state = 3
filtered_state_means = np.zeros((n_timesteps, n_dim_state))
filtered_state_covariances = np.zeros((n_timesteps, n_dim_state, n_dim_state))
# Kalman-Filter initialization
kf = KalmanFilter(transition_matrices = F,
observation_matrices = H,
transition_covariance = Q,
observation_covariance = R,
initial_state_mean = X0,
initial_state_covariance = P0)
# iterative estimation for each new measurement
for t in range(n_timesteps):
if t == 0:
filtered_state_means[t] = X0
filtered_state_covariances[t] = P0
else:
filtered_state_means[t], filtered_state_covariances[t] = (
kf.filter_update(
filtered_state_means[t-1],
filtered_state_covariances[t-1],
observation = X[t])
)
position_sigma = np.sqrt(filtered_state_covariances[:, 0, 0]);
# plot of the resulted trajectory
plt.plot(Time, filtered_state_means[:, 0], "g-", label="Filtered position", markersize=1)
plt.plot(Time, filtered_state_means[:, 0] + position_sigma, "r--", label="+ sigma", markersize=1)
plt.plot(Time, filtered_state_means[:, 0] - position_sigma, "r--", label="- sigma", markersize=1)
plt.grid()
plt.legend(loc="upper left")
plt.xlabel("Time (s)")
plt.ylabel("Position (m)")
plt.show()
UPDATE
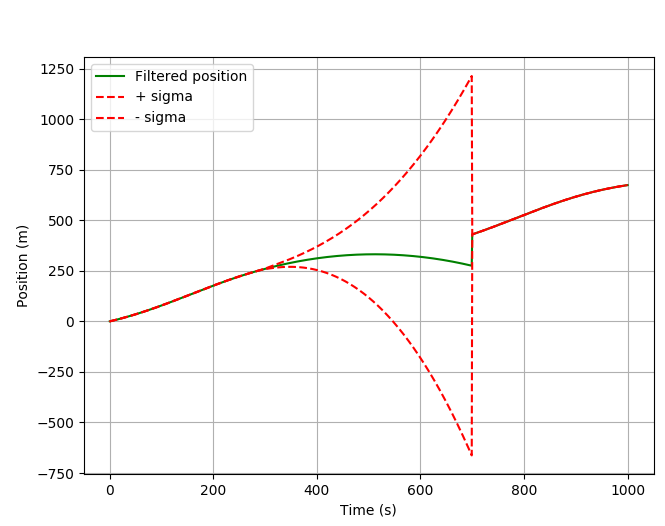
It looks even more interesting if you mask a longer period (300:700).
![filter position without gps signal]()
As you can see the position goes back. It happens because of the transition matrix F, which binds the prediction for position, velocity and acceleration.
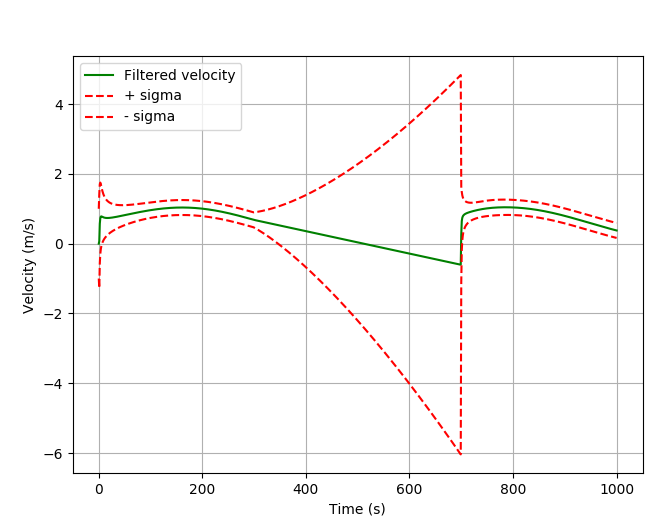
If you have a look at the velocity state, it explains the decreasing position.
![velocity estimation using pykalman and lost gps signal]()
At the time point 300 s the acceleration freezes. The velocity goes down with a constant slope and crosses the 0 value. After this time point the position has to go back.
To plot the velocity use the following code:
velocity_sigma = np.sqrt(filtered_state_covariances[:, 1, 1]);
# plot of the estimated velocity
plt.plot(Time, filtered_state_means[:, 1], "g-", label="Filtered velocity", markersize=1)
plt.plot(Time, filtered_state_means[:, 1] + velocity_sigma, "r--", label="+ sigma", markersize=1)
plt.plot(Time, filtered_state_means[:, 1] - velocity_sigma, "r--", label="- sigma", markersize=1)
plt.grid()
plt.legend(loc="upper left")
plt.xlabel("Time (s)")
plt.ylabel("Velocity (m/s)")
plt.show()