Way to contour outer edge of selected grid region in Python

Question

I have the following code:

import numpy as np
import matplotlib.pyplot as plt

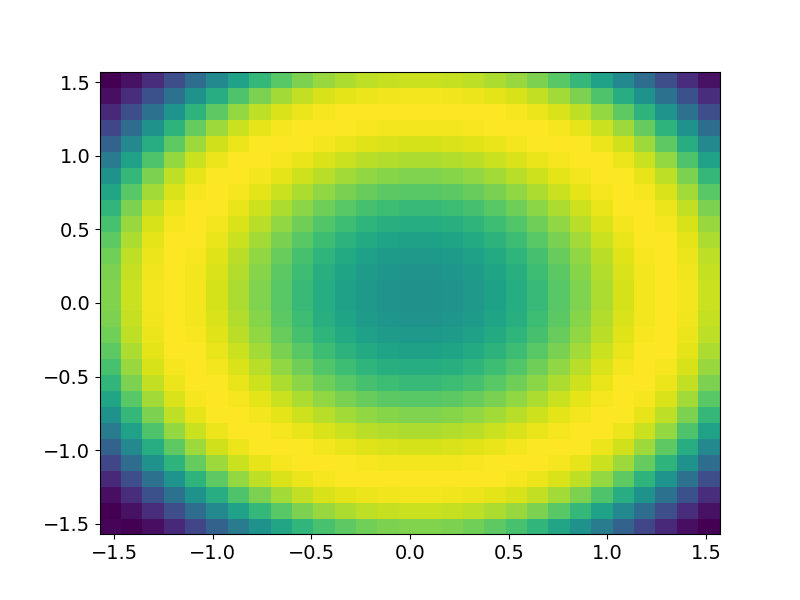
x = np.linspace(-np.pi/2, np.pi/2, 30)
y = np.linspace(-np.pi/2, np.pi/2, 30)
x,y = np.meshgrid(x,y)

z = np.sin(x**2+y**2)[:-1,:-1]

fig,ax = plt.subplots()
ax.pcolormesh(x,y,z)

Which gives this image:

Now lets say I want to highlight the edge certain grid boxes:

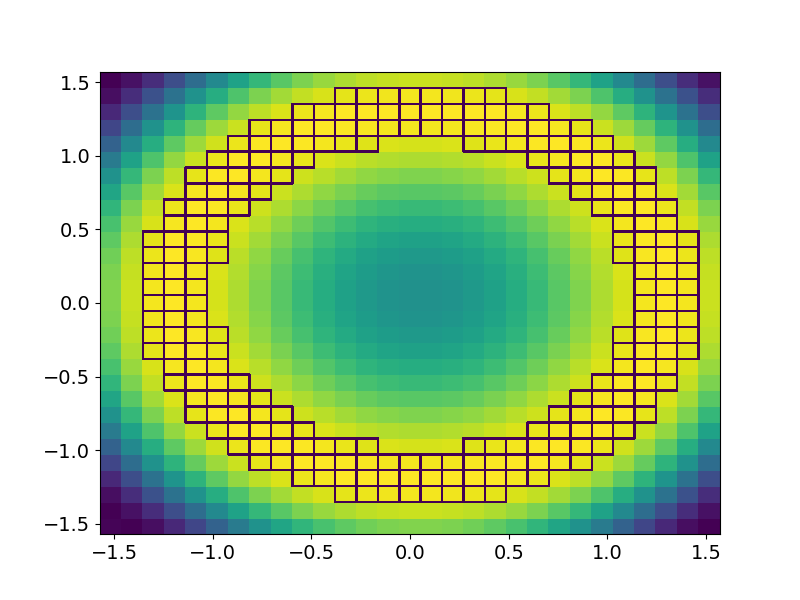
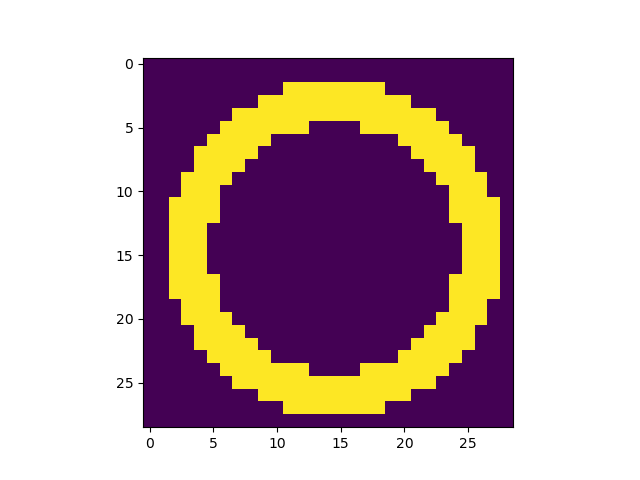
highlight = (z > 0.9)

I could use the contour function, but this would result in a "smoothed" contour. I just want to highlight the edge of a region, following the edge of the grid boxes.

The closest I've come is adding something like this:

highlight = np.ma.masked_less(highlight, 1)

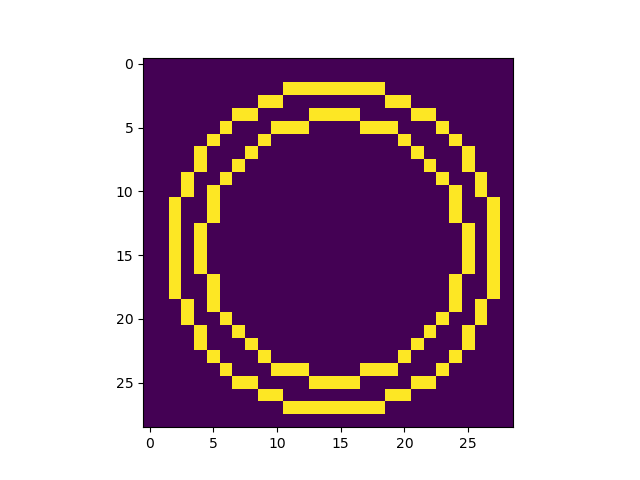
ax.pcolormesh(x, y, highlight, facecolor = 'None', edgecolors = 'w')

Which gives this plot:

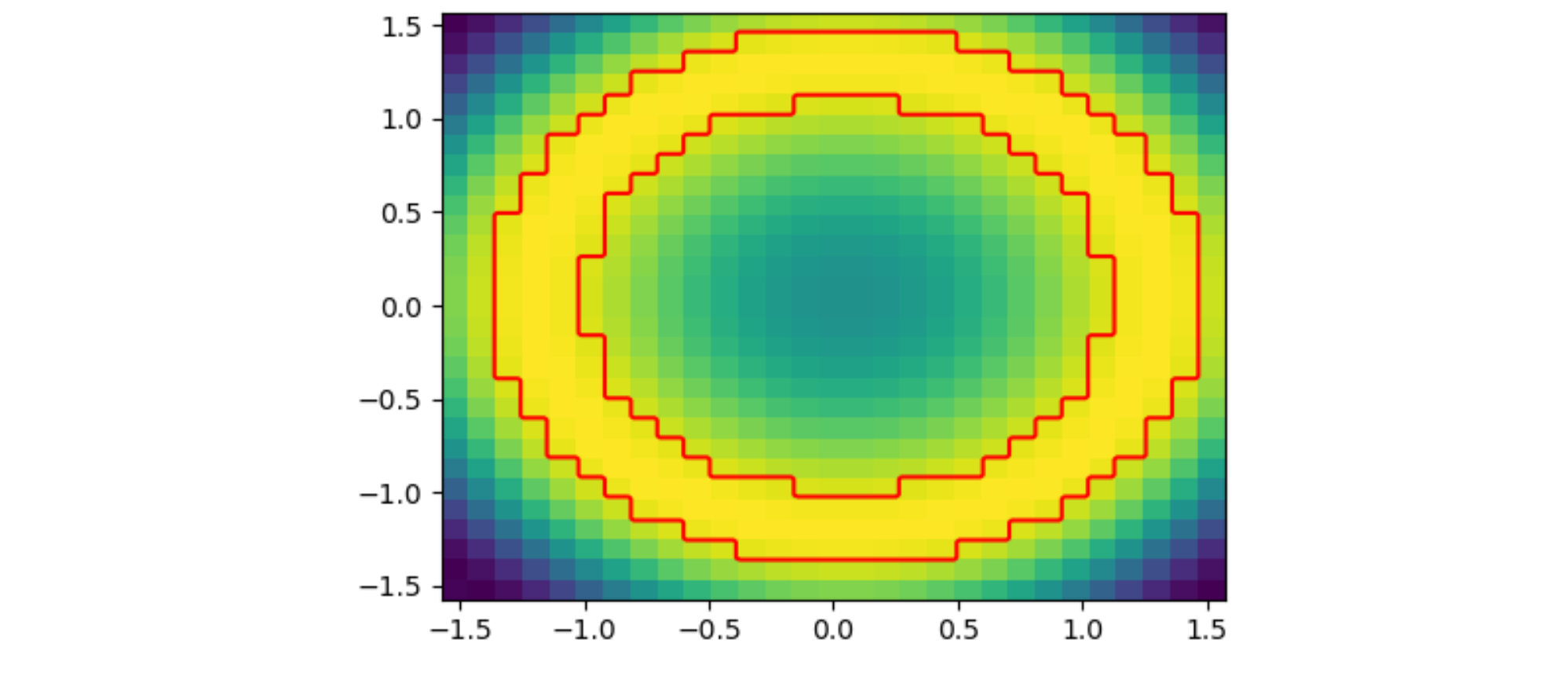
Which is close, but what I really want is for only the outer and inner edges of that "donut" to be highlighted.

So essentially I am looking for some hybrid of the contour and pcolormesh functions - something that follows the contour of some value, but follows grid bins in "steps" rather than connecting point-to-point. Does that make sense?

Side note: In the pcolormesh arguments, I have edgecolors = 'w', but the edges still come out to be blue. Whats going on there?

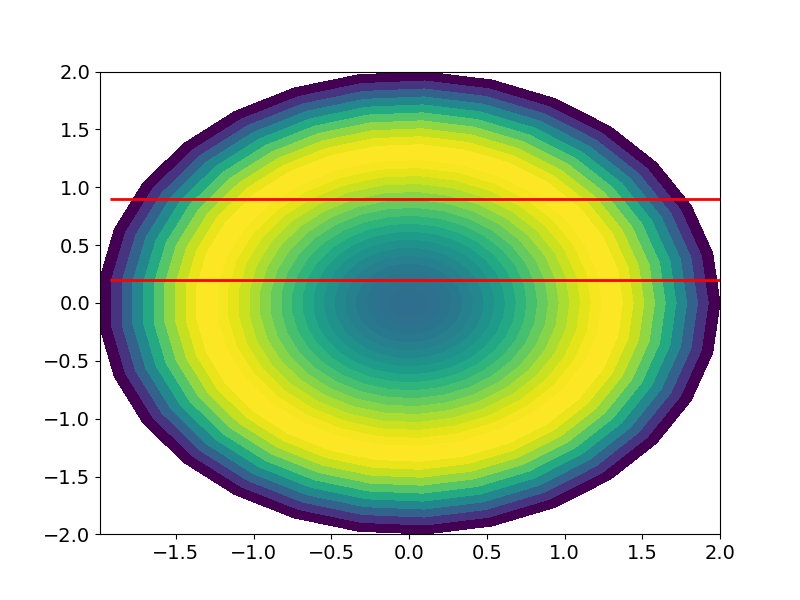
EDIT: JohanC's initial answer using add_iso_line() works for the question as posed. However, the actual data I'm using is a very irregular x,y grid, which cannot be converted to 1D (as is required for add_iso_line().

I am using data which has been converted from polar coordinates (rho, phi) to cartesian (x,y). The 2D solution posed by JohanC does not appear to work for the following case:

import numpy as np
import matplotlib.pyplot as plt
from scipy import ndimage

def pol2cart(rho, phi):
    x = rho * np.cos(phi)
    y = rho * np.sin(phi)
    return(x, y)

phi = np.linspace(0,2*np.pi,30)
rho = np.linspace(0,2,30)

pp, rr = np.meshgrid(phi,rho)

xx,yy = pol2cart(rr, pp)

z = np.sin(xx**2 + yy**2)

scale = 5
zz = ndimage.zoom(z, scale, order=0)

fig,ax = plt.subplots()
ax.pcolormesh(xx,yy,z[:-1, :-1])

xlim = ax.get_xlim()
ylim = ax.get_ylim()
xmin, xmax = xx.min(), xx.max()
ymin, ymax = yy.min(), yy.max()
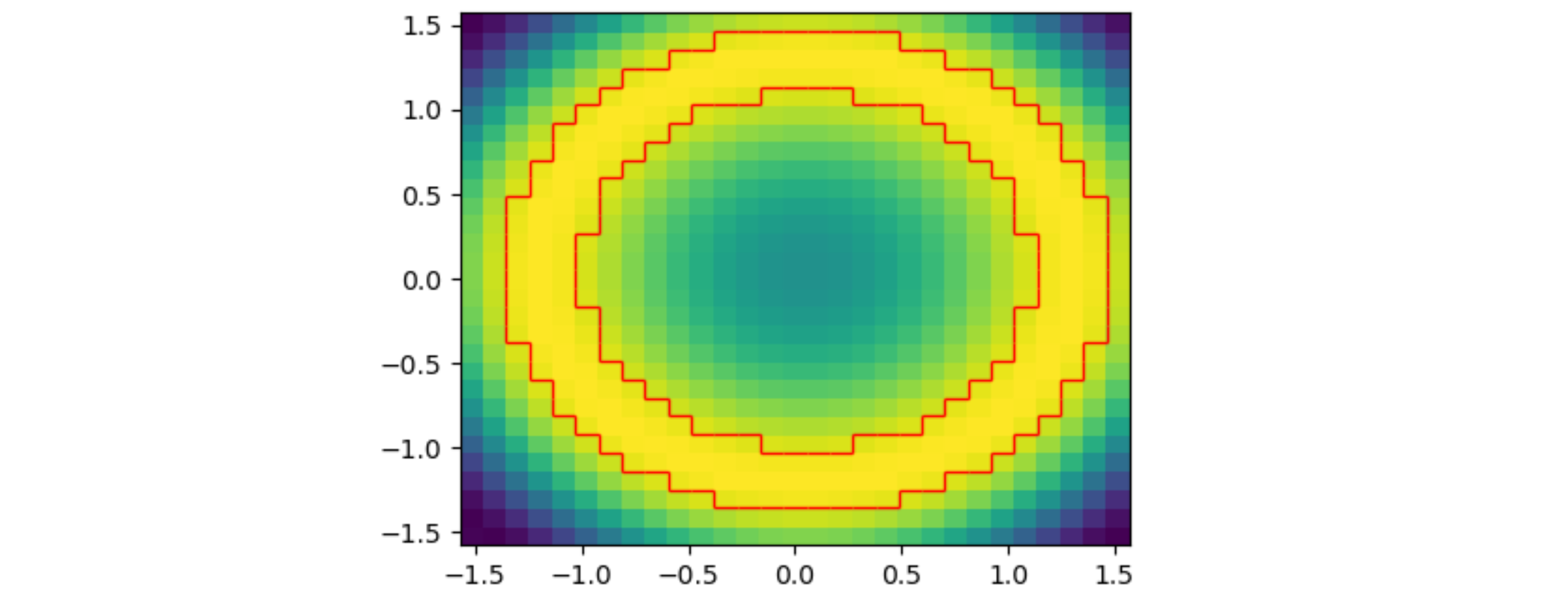
ax.contour(np.linspace(xmin,xmax, zz.shape[1]) + (xmax-xmin)/z.shape[1]/2,
           np.linspace(ymin,ymax, zz.shape[0]) + (ymax-ymin)/z.shape[0]/2,
           np.where(zz < 0.9, 0, 1), levels=[0.5], colors='red')
ax.set_xlim(*xlim)
ax.set_ylim(*ylim)

Comprise

Yes, it is clear and very useful question – Micrometeorite

z[z>0.9] = 0 or z[z>0.9] = 1 to change the values so they are different. Note that pyplot automatically is asigning a color map. You may want to use a grayscale color map. Or you may want to just use cv2.imshow() to see it in grayscale. Then you can convert to 3 channels and make the emphasis red z1=cv2.merge([z,z,z]) and then z1[z>0.9]=(255,255,255) – Hypallage

Answer 1

This post shows a way to draw such lines. As it is not straightforward to adapt to the current pcolormesh, the following code demonstrates a possible adaption. Note that the 2d versions of x and y have been renamed, as the 1d versions are needed for the line segments.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

x = np.linspace(-np.pi / 2, np.pi / 2, 30)
y = np.linspace(-np.pi / 2, np.pi / 2, 30)
xx, yy = np.meshgrid(x, y)

z = np.sin(xx ** 2 + yy ** 2)[:-1, :-1]

fig, ax = plt.subplots()
ax.pcolormesh(x, y, z)

def add_iso_line(ax, value, color):
    v = np.diff(z > value, axis=1)
    h = np.diff(z > value, axis=0)

    l = np.argwhere(v.T)
    vlines = np.array(list(zip(np.stack((x[l[:, 0] + 1], y[l[:, 1]])).T,
                               np.stack((x[l[:, 0] + 1], y[l[:, 1] + 1])).T)))
    l = np.argwhere(h.T)
    hlines = np.array(list(zip(np.stack((x[l[:, 0]], y[l[:, 1] + 1])).T,
                               np.stack((x[l[:, 0] + 1], y[l[:, 1] + 1])).T)))
    lines = np.vstack((vlines, hlines))
    ax.add_collection(LineCollection(lines, lw=1, colors=color))

add_iso_line(ax, 0.9, 'r')
plt.show()

Here is an adaption of the second answer, which can work with only 2d arrays:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
from scipy import ndimage

x = np.linspace(-np.pi / 2, np.pi / 2, 30)
y = np.linspace(-np.pi / 2, np.pi / 2, 30)
x, y = np.meshgrid(x, y)

z = np.sin(x ** 2 + y ** 2)

scale = 5
zz = ndimage.zoom(z, scale, order=0)

fig, ax = plt.subplots()
ax.pcolormesh(x, y,  z[:-1, :-1] )
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xmin, xmax = x.min(), x.max()
ymin, ymax = y.min(), y.max()
ax.contour(np.linspace(xmin,xmax, zz.shape[1]) + (xmax-xmin)/z.shape[1]/2,
           np.linspace(ymin,ymax, zz.shape[0]) + (ymax-ymin)/z.shape[0]/2,
           np.where(zz < 0.9, 0, 1), levels=[0.5], colors='red')
ax.set_xlim(*xlim)
ax.set_ylim(*ylim)
plt.show()

Pivotal

Ok, so this answers the question as posed. However, I guess I simplified it too much. In the dataset I'm actually working with, x and y are not a on a regular grid - I can't change them into 1-D. Should I make a new question? – Comprise

You probably can extract the 1d versions from the 2d versions. Something like x1d = x[0,:] and y1d = y[:,0]. Feel free to extend your current question (or add a new one). – Pivotal

The proposed 2D solution does not work for my case. I've updated the original question with anew example. – Comprise

Answer 2

I'll try to refactor add_iso_line method in order to make it more clear an open for optimisations. So, at first, there comes a must-do part:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

x = np.linspace(-np.pi/2, np.pi/2, 30)
y = np.linspace(-np.pi/2, np.pi/2, 30)
x, y = np.meshgrid(x,y)
z = np.sin(x**2+y**2)[:-1,:-1]

fig, ax = plt.subplots()
ax.pcolormesh(x,y,z)
xlim, ylim = ax.get_xlim(), ax.get_ylim()
highlight = (z > 0.9)

Now highlight is a binary array that looks like this: After that we can extract indexes of True cells, look for False neighbourhoods and identify positions of 'red' lines. I'm not comfortable enough with doing it in a vectorised manner (like here in add_iso_line method) so just using simple loop:

lines = []
cells = zip(*np.where(highlight))
for x, y in cells:
    if x == 0 or highlight[x - 1, y] == 0: lines.append(([x, y], [x, y + 1]))
    if x == highlight.shape[0] or highlight[x + 1, y] == 0: lines.append(([x + 1, y], [x + 1, y + 1]))
    if y == 0 or highlight[x, y - 1] == 0: lines.append(([x, y], [x + 1, y]))
    if y == highlight.shape[1] or highlight[x, y + 1] == 0: lines.append(([x, y + 1], [x + 1, y + 1]))

And, finally, I resize and center coordinates of lines in order to fit with pcolormesh:

lines = (np.array(lines) / highlight.shape - [0.5, 0.5]) * [xlim[1] - xlim[0], ylim[1] - ylim[0]]
ax.add_collection(LineCollection(lines, colors='r'))
plt.show()

In conclusion, this is very similar to JohanC solution and, in general, slower. Fortunately, we can reduce amount of cells significantly, extracting contours only using python-opencv package:

import cv2
highlight = highlight.astype(np.uint8)
contours, hierarchy = cv2.findContours(highlight, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cells = np.vstack(contours).squeeze()

This is an illustration of cells being checked:

Micrometeorite