Javascript code for finding min distance from a point to polygon (as defined by html area)

Question

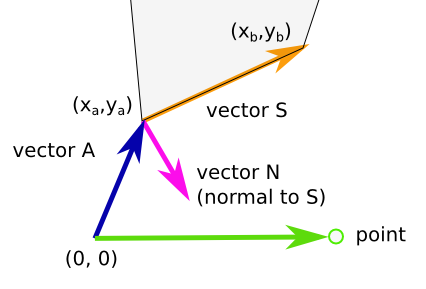
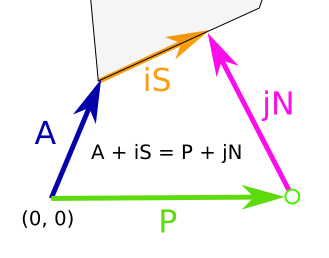
I have an image map with multiple areas defined, all as polygons

I would like to calculate the distance from a point on the image (typically given by the user clicking on the image) to the closes point on the outer edge of a given area.

For my case one can make the assumption that none of the edges of the polygon intersect, thus making the task a bit easyer

Detecting if the point is inside, on or outside the area/polygon is also interesting, eg by having a negative distance if the point is inside the polygon, 0 if its on the edge.

But this is not that important for me, as it easy to detect this given that the point is given by the user clicking on the image.

---

The generic solution for this problem is given here - but i wonder if anyone already have a implementation in javascript for solving this with image maps and areas

I would like to do something like:

var distance = calculateDistancePointToArea( xCoord, yCoord, areaId );

And it would be an extra bonus if this worked for all the shapes possible for an area: rect, circle and poly

Deus

Answer 1

I wrote a function for generic coordinates, and if you need, you may convert it to work with your HTML poly.

A very simple solution: solve an equasion for each pair of poly vertices.

An algorithm for one segment of the polygon (gray in the picture) with points a and b:

• vector A is just point a coordinates
• vector S(egment) = b - a
• vector N is normal to S (-ys, xs)
• vector P is coordinates of point

You want to check the length of normal from point to Segment and make sure the target point is inside Segment.

Here's the equasion you want to solve:

In the solution, i must be between 0 and 1. If it is, then the distance is |iN| and the point is P + iN, otherwise it's the closest between vertices (a & b). Then you can find the closest point among those for each edge.

Here's a Javascript code that searches for closest distance, but it should be easy to modify for closest point:

function vlen(vector) {
  return Math.sqrt(vector[0]*vector[0] + vector[1] * vector[1]);
}

function vsub(v1, v2) {
  return [v1[0] - v2[0], v1[1] - v2[1]];
}

function vscale(vector, factor) {
  return [vector[0] * factor, vector[1] * factor];
}

function vnorm(v) {
  return [-v[1], v[0]];
}

function distance_to_poly(point, poly) {
  var dists = $.map(poly, function(p1, i) {
    var prev = (i == 0 ? poly.length : i) - 1,
        p2 = poly[prev],
        line = vsub(p2, p1);

    if (vlen(line) == 0)
      return vlen(vsub(point, p1));

    var norm = vnorm(line),
        x1 = point[0],
        x2 = norm[0],
        x3 = p1[0],
        x4 = line[0],
        y1 = point[1],
        y2 = norm[1],
        y3 = p1[1],
        y4 = line[1],

        j = (x3 - x1 - x2 * y3 / y2 + x2 * y1 / y2) / (x2 * y4 / y2 - x4),
        i;

      if (j < 0 || j > 1)
        return Math.min(
          vlen(vsub(point, p1)),
          vlen(vsub(point, p2)));

      i = (y3 + j * y4 - y1) / y2;

      return vlen(vscale(norm, i));
  });

  return Math.min.apply(null, dists);
}

Risinger

Answer 2

here's the function to calculate distance between two coordinates in javascript.

function(calculateDistancePointToArea(x2, y2, areaId))
{
    var el1 = document.getElementById(areaId);
    var off1 = getOffset(el1);
    // center
    var x1 = off1.left;
    var y1 = off1.top;
    // distance
    var length = Math.sqrt(((x2-x1) * (x2-x1)) + ((y2-y1) * (y2-y1)));       
}

function getOffset( el ) {
    var _x = 0;
    var _y = 0;
    var _w = el.offsetWidth|0;
    var _h = el.offsetHeight|0;
    while( el && !isNaN( el.offsetLeft ) && !isNaN( el.offsetTop ) ) {
        _x += el.offsetLeft - el.scrollLeft;
        _y += el.offsetTop - el.scrollTop;
        el = el.offsetParent;
    }
    return {
        top: _y,
        left: _x,
        width: _w,
        height: _h
    };
}

Hope it gives you an idea and helps.

Homemade