Matlab: patch area between two curves which depend on the curves values

Question

I'm trying to fill an area between two curves with respect to a function which depends on the values of the curves.

Here is the code of what I've managed to do so far

    i=50;
cc = @(xx,x,y) 1./(1+(exp(-xx)/(exp(-x)-exp(-y))));
n_vec = 2:0.1:10;
x_vec = linspace(2,10,length(n_vec));
y_vec = abs(sin(n_vec));
N=[n_vec,fliplr(n_vec)];  
X=[x_vec,fliplr(y_vec)];
figure(1)
subplot(2,1,1)
hold on
plot(n_vec,x_vec,n_vec,y_vec)
hp = patch(N,X,'b')
plot([n_vec(i) n_vec(i)],[x_vec(i),y_vec(i)],'linewidth',5)
xlabel('n'); ylabel('x')
subplot(2,1,2)

xx = linspace(y_vec(i),x_vec(i),100);
plot(xx,cc(xx,y_vec(i),x_vec(i)))
xlabel('x'); ylabel('c(x)')

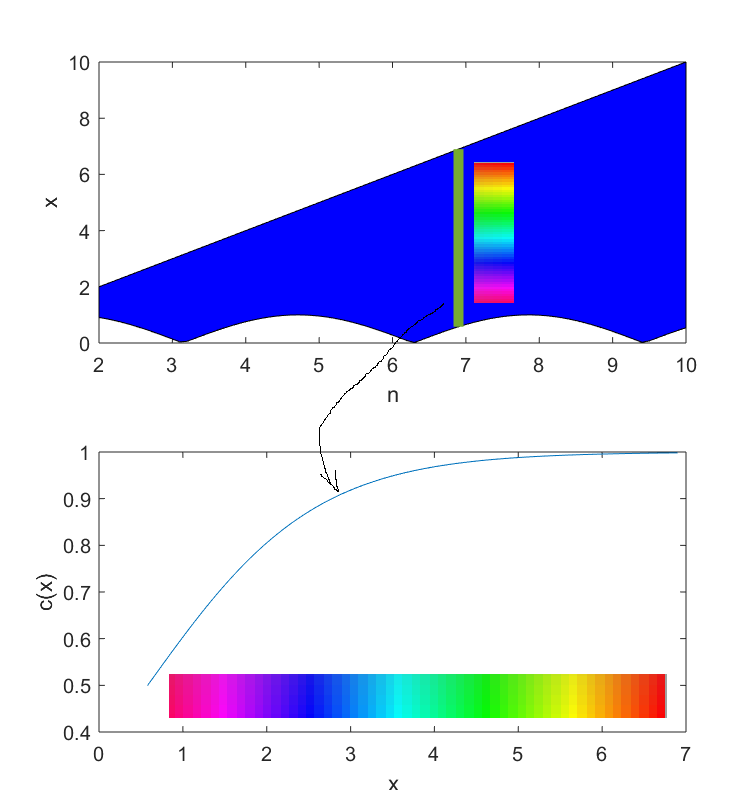
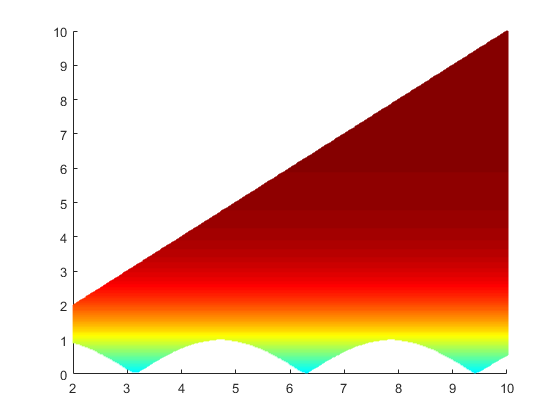
This code produces the following graph

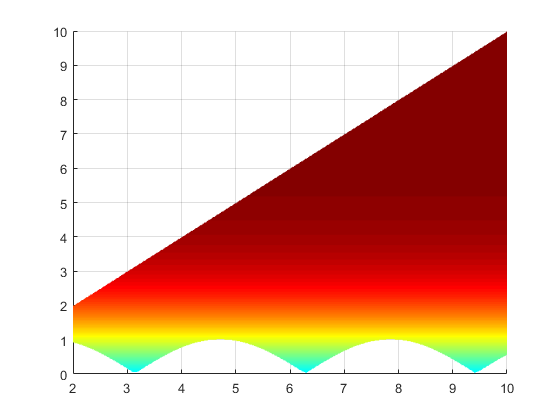
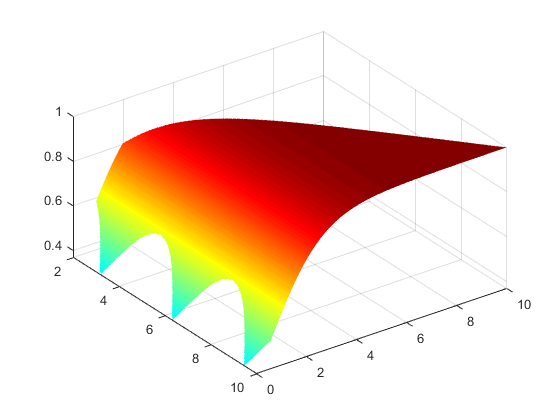
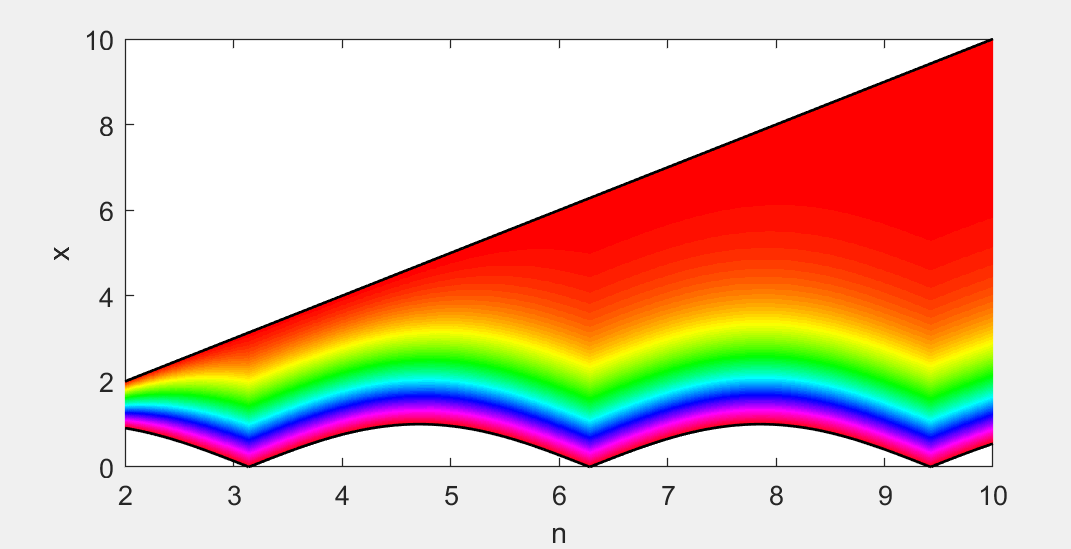
The color code which I've added represent the color coding that each line (along the y axis at a point on the x axis) from the area between the two curves should be.

Overall, the entire area should be filled with a gradient color which depends on the values of the curves.

I've assisted the following previous questions but could not resolve a solution

MATLAB fill area between lines

Patch circle by a color gradient

Filling between two curves, according to a colormap given by a function MATLAB

NOTE: there is no importance to the functional form of the curves, I would prefer an answer which refers to two general arrays which consist the curves.

Folia

Answer 1

The surf plot method

1. The same as the scatter plot method, i.e. generate a point grid.

y = [x_vec(:); y_vec(:)];
resolution = [500,500];
px = linspace(min(n_vec), max(n_vec), resolution(1));
py = linspace(min(y), max(y), resolution(2));
[px, py] = meshgrid(px, py);

2. Generate a logical array indicating whether the points are inside the polygon, but no need to extract the points:

in = inpolygon(px, py, N, X);

3. Generate Z. The value of Z indicates the color to use for the surface plot. Hence, it is generated using the your function cc.

pz = 1./(1+(exp(-py_)/(exp(-y_vec(i))-exp(-x_vec(i)))));
pz = repmat(pz',1,resolution(2));

4. Set Z values for points outside the area of interest to NaN so MATLAB won't plot them.

pz(~in) = nan;

5. Generate a bounded colourmap (delete if you want to use full colour range)

% generate colormap
c = jet(100);
[s,l] = bounds(pz,'all');
s = round(s*100);
l = round(l*100);
if s ~= 0
    c(1:s,:) = [];
end
if l ~= 100
    c(l:100,:) = [];
end

6. Finally, plot.

figure;
colormap(jet)
surf(px,py,pz,'edgecolor','none');
view(2) % x-y view

Feel free to turn the image arround to see how it looks like in the Z-dimention - beautiful :)

---

Full code to test:

i=50;
cc = @(xx,x,y) 1./(1+(exp(-xx)/(exp(-x)-exp(-y))));
n_vec = 2:0.1:10;
x_vec = linspace(2,10,length(n_vec));
y_vec = abs(sin(n_vec));

% generate grid
y = [x_vec(:); y_vec(:)];
resolution = [500,500];
px_ = linspace(min(n_vec), max(n_vec), resolution(1));
py_ = linspace(min(y), max(y), resolution(2));
[px, py] = meshgrid(px_, py_);

% extract points
in = inpolygon(px, py, N, X);

% generate z
pz = 1./(1+(exp(-py_)/(exp(-y_vec(i))-exp(-x_vec(i)))));
pz = repmat(pz',1,resolution(2));
pz(~in) = nan;

% generate colormap
c = jet(100);
[s,l] = bounds(pz,'all');
s = round(s*100);
l = round(l*100);
if s ~= 0
    c(1:s,:) = [];
end
if l ~= 100
    c(l:100,:) = [];
end

% plot
figure;
colormap(c)
surf(px,py,pz,'edgecolor','none');
view(2)

Shrift

Answer 2

You can use imagesc and meshgrids. See comments in the code to understand what's going on.

Downsample your data

% your initial upper and lower boundaries
n_vec_long = linspace(2,10,1000000);

f_ub_vec_long = linspace(2, 10, length(n_vec_long));
f_lb_vec_long = abs(sin(n_vec_long));

% downsample
n_vec = linspace(n_vec_long(1), n_vec_long(end), 1000); % for example, only 1000 points

% get upper and lower boundary values for n_vec
f_ub_vec = interp1(n_vec_long, f_ub_vec_long, n_vec); 
f_lb_vec = interp1(n_vec_long, f_lb_vec_long, n_vec); 

% x_vec for the color function
x_vec = 0:0.01:10;

Plot the data

% create a 2D matrix with N and X position
[N, X] = meshgrid(n_vec, x_vec);

% evaluate the upper and lower boundary functions at n_vec
% can be any function at n you want (not tested for crossing boundaries though...)
f_ub_vec = linspace(2, 10, length(n_vec));
f_lb_vec = abs(sin(n_vec));

% make these row vectors into matrices, to create a boolean mask
F_UB = repmat(f_ub_vec, [size(N, 1) 1]);
F_LB = repmat(f_lb_vec, [size(N, 1) 1]);

% create a mask based on the upper and lower boundary functions
mask = true(size(N));
mask(X > F_UB | X < F_LB) = false;

% create data matrix
Z = NaN(size(N));

% create function that evaluates the color profile for each defined value 
% in the vectors with the lower and upper bounds
zc = @(X, ub, lb) 1 ./ (1 + (exp(-X) ./ (exp(-ub) - exp(-lb))));
CData = zc(X, f_lb_vec, f_ub_vec); % create the c(x) at all X

% put the CData in Z, but only between the lower and upper bound.
Z(mask) = CData(mask);

% normalize Z along 1st dim
Z = normalize(Z, 1, 'range'); % get all values between 0 and 1 for colorbar

% draw a figure!
figure(1); clf;
ax = axes;                          % create some axes
sc = imagesc(ax, n_vec, x_vec, Z);  % plot the data
ax.YDir = 'normal' % set the YDir to normal again, imagesc reverses it by default;

xlabel('n')
ylabel('x')

This already looks kinda like what you want, but let's get rid of the blue area outside the boundaries. This can be done by creating an 'alpha mask', i.e. set the alpha value for all pixels outside the previously defined mask to 0:

figure(2); clf;
ax = axes;                          % create some axes
hold on;
sc = imagesc(ax, n_vec, x_vec, Z);  % plot the data
ax.YDir = 'normal' % set the YDir to normal again, imagesc reverses it by default;

% set a colormap 
colormap(flip(hsv(100)))

% set alpha for points outside mask
Calpha = ones(size(N));
Calpha(~mask) = 0;
sc.AlphaData = Calpha;

% plot the other lines
plot(n_vec, f_ub_vec, 'k', n_vec, f_lb_vec, 'k' ,'linewidth', 1)

% set axis limits
xlim([min(n_vec), max(n_vec)])
ylim([min(x_vec), max(x_vec)])

Exophthalmos

thanks for the answer, but this does not help me much. first, the code can not be applied on a large data set. second, and the most important of all, the color gradient should be only between the region between the two curves. meaning that the distance between the two curves defines how sharp is the gradient. In your result it is the same for all values of n – Folia

@Folia I see, it only is using the lower boundary at the moment. Can you show in your question what kind of data set you want to use this for (dimensions, code to generate sample data...). – Exophthalmos

@Folia see the update, the color value follows the curve. If this is still not what you want, could you illustrate a bit more clear what you want to achieve? Your colorbar in the plot of c(x) indicates that you want a linearly increasing colormap, while the curve itself isn't. – Exophthalmos

is it possible to upload MAT data files here, I can send a sample. – Folia

making the code won't make a different, think of applying it to vectors of length ~ 1000000. The mesh will be too much for the memory, maybe using the patch command is better? – Folia

@Folia Well, indeed applying this to vectors of that length is not going to work, but you also don't have that many pixels on your screen in one direction, so you would't be able to see the fine detail anyway. You can interpolate/downsample your data, I will add this to the answer. – Exophthalmos

I believe patch only allows linear interpolation between the color values at the edges, thus not fulfilling your c(x) color function requirement. – Exophthalmos

Answer 3

there is no importance to the functional form of the curves, I would prefer an answer which refers to two general arrays which consist the curves.

It is difficult to achieve this using patch.

However, you may use scatter plots to "fill" the area with coloured dots. Alternatively, and probably better, use surf plot and generate z coordinates using your cc function (See my seperate solution).

The scatter plot method

1. First, make a grid of points (resolution 500*500) inside the rectangular space bounding the two curves.

y = [x_vec(:); y_vec(:)];
resolution = [500,500];
px = linspace(min(n_vec), max(n_vec), resolution(1));
py = linspace(min(y), max(y), resolution(2));
[px, py] = meshgrid(px, py);

figure; 
scatter(px(:), py(:), 1, 'r');

The not-interesting figure of the point grid:

2. Next, extract the points inside the polygon defined by the two curves.

in = inpolygon(px, py, N, X);
px = px(in);
py = py(in);

hold on;
scatter(px, py, 1, 'k');

Black points are inside the area:

3. Finally, create color and plot the nice looking gradient colour figure.

% create color for the points
cid = 1./(1+(exp(-py)/(exp(-y_vec(i))-exp(-x_vec(i)))));
c = jet(101);
c = c(round(cid*100)+1,:); % +1 to avoid zero indexing

% plot
figure;
scatter(px,py,16,c,'filled','s'); % use size 16, filled square markers.

Note that you may need a fairly dense grid of points to make sure the white background won't show up. You may also change the point size to a bigger value (won't impact performance).

Of cause, you may use patch to replace scatter but you will need to work out the vertices and face ids, then you may patch each faces separately with patch('Faces',F,'Vertices',V). Using patch this way may impact performance.

---

Complete code to test:

i=50;
cc = @(xx,x,y) 1./(1+(exp(-xx)/(exp(-x)-exp(-y))));
n_vec = 2:0.1:10;
x_vec = linspace(2,10,length(n_vec));
y_vec = abs(sin(n_vec));

% generate point grid
y = [x_vec(:); y_vec(:)];
resolution = [500,500];
px_ = linspace(min(n_vec), max(n_vec), resolution(1));
py_ = linspace(min(y), max(y), resolution(2));
[px, py] = meshgrid(px_, py_);

% extract points
in = inpolygon(px, py, N, X);
px = px(in);
py = py(in);


% generate color
cid = 1./(1+(exp(-py)/(exp(-y_vec(i))-exp(-x_vec(i)))));
c = jet(101);
c = c(round(cid*100)+1,:); % +1 to avoid zero indexing

% plot
figure;
scatter(px,py,16,c,'filled','s');

Shrift