Frequencies when performing FFT with Eigen::FFT

Question

I'm currently trying to figure out how exactly to use Eigen's FFT algorithm. Let us a assume I have a function

std::complex<double> f(std::complex<double> const & t){
    return std::sin(t);
}

I then compute with this function

Eigen::VectorXcd time(1000);
Eigen::VectorXcd f_values(1000);
for(int u = 0; u < 1000; ++u){
    time(u) = u* 2. * M_PI / 1000;
    f_values(u) = f(time(u));
}

I'd now like to compute the Fourier transformation of f_values, so I do

Eigen::FFT<double> fft;
Eigen::VectorXcd f_freq(1000);
fft.fwd(f_freq, f_values);

Now I would like to plot this, but to do this I need the frequencies at which f_freq was evaluated, but I don't really know how to obtain these frequencies. So my question boils down to finding the Eigen::VectorXcd containing the frequencies to plot things like this 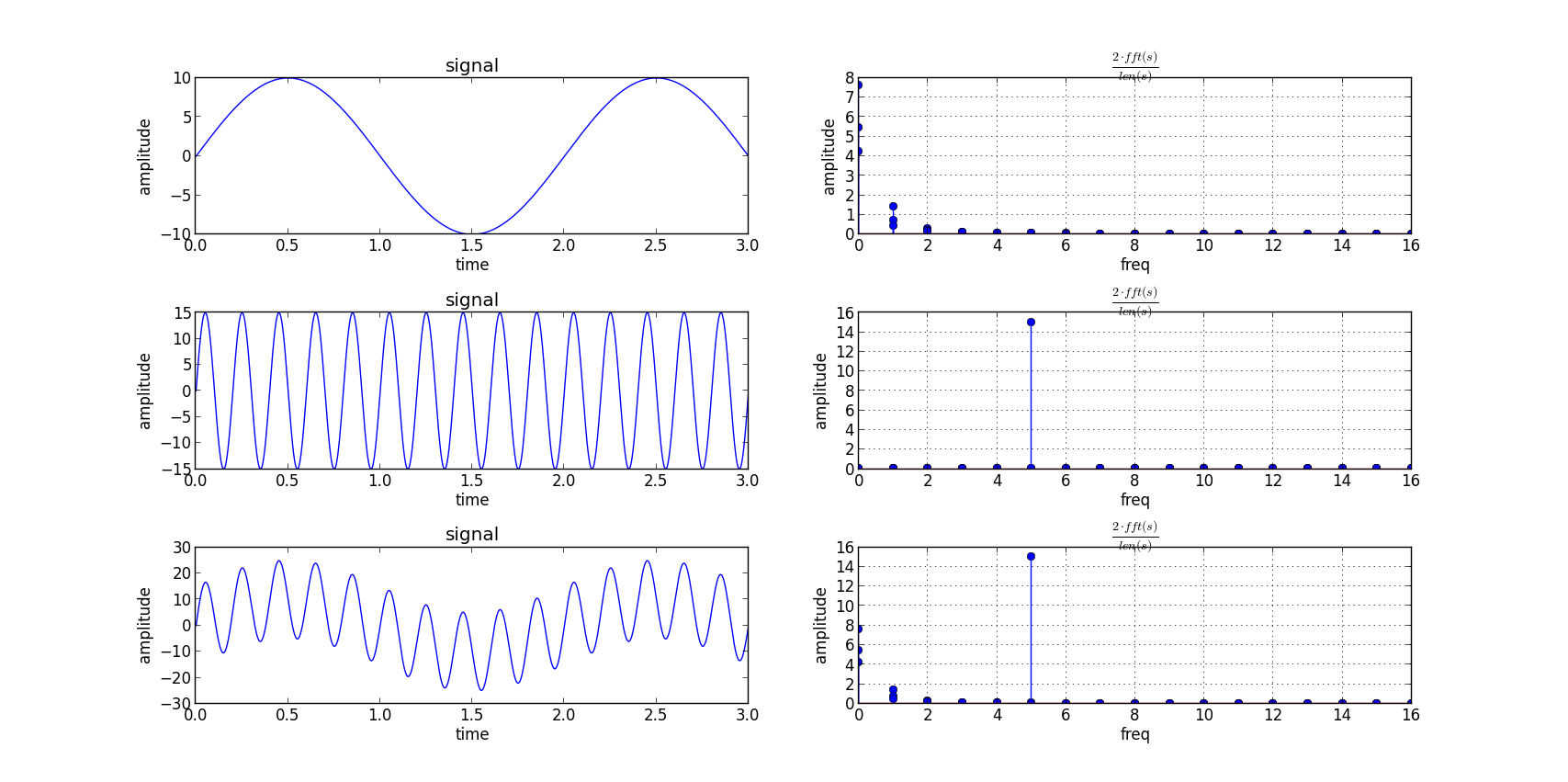(I'm sorry for using a picture as description, but I think its much clearer this way then if I tried to describe it with words... The amplitude from the plot should correspond to my f_freq and what I looking for is the values of freq in the picture...).

Here are the above code snippets put into a single file:

#include <eigen3/Eigen/Dense>
#include <eigen3/unsupported/Eigen/FFT>
#include <complex>
#include <cmath>

std::complex<double> f(std::complex<double> const & t){
     return std::sin(t);
}

int main(){
    Eigen::VectorXcd time(1000);
    Eigen::VectorXcd f_values(1000);
    for(int u = 0; u < 1000; ++u){
        time(u) = u* 2. * M_PI / 1000;
        f_values(u) = f(time(u));
    }

    Eigen::FFT<double> fft;
    Eigen::VectorXcd f_freq(1000);
    fft.fwd(f_freq, f_values);
    //freq = ....
}

---

I implemented one of the suggested answers as follows:

#include <eigen3/Eigen/Dense>
#include <eigen3/unsupported/Eigen/FFT>
#include <complex>
#include <cmath>
#include <iostream>
#include <fstream>

std::complex<double> f(std::complex<double> const & t){
     return std::sin(1.*t);
}

int main(){
    std::ofstream freq_out("frequencies.txt");
    std::ofstream f_freq_out("f_freq.txt");

    unsigned const N = 1000.;
    Eigen::VectorXcd time(N);
    Eigen::VectorXcd f_values(N);
    for(int u = 0; u < N; ++u){
        time(u) = u* 2. * M_PI / double(N);
        f_values(u) = f(time(u));
    }

    Eigen::FFT<double> fft;
    Eigen::VectorXcd f_freq(N);
    Eigen::VectorXd freq(N);
    fft.fwd(f_freq, f_values);

    double const Ts = 2. * M_PI/double(N);
    double const Fs = 1./Ts;

    for(int u = 0; u < N; ++u){
        freq(u) = Fs * u / double(N);
    }

    freq_out << freq; 
    f_freq_out << f_freq.cwiseAbs();
}

which results in the following plot 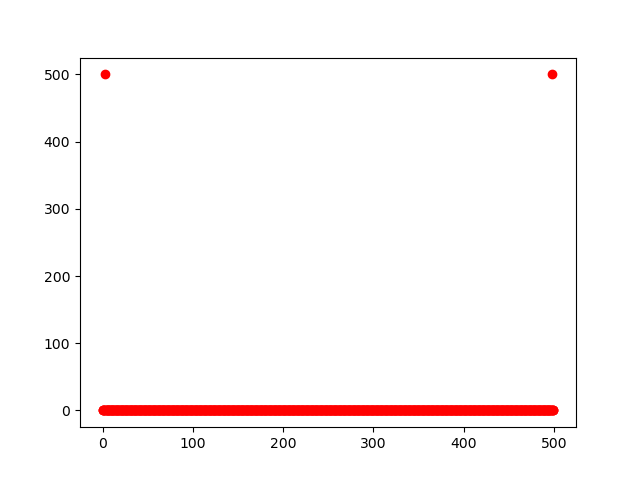This seems a bit off.. The scaling certainly makes not much sense, but also the fact that there are two values that spike makes me a bit skeptical..

Siegel

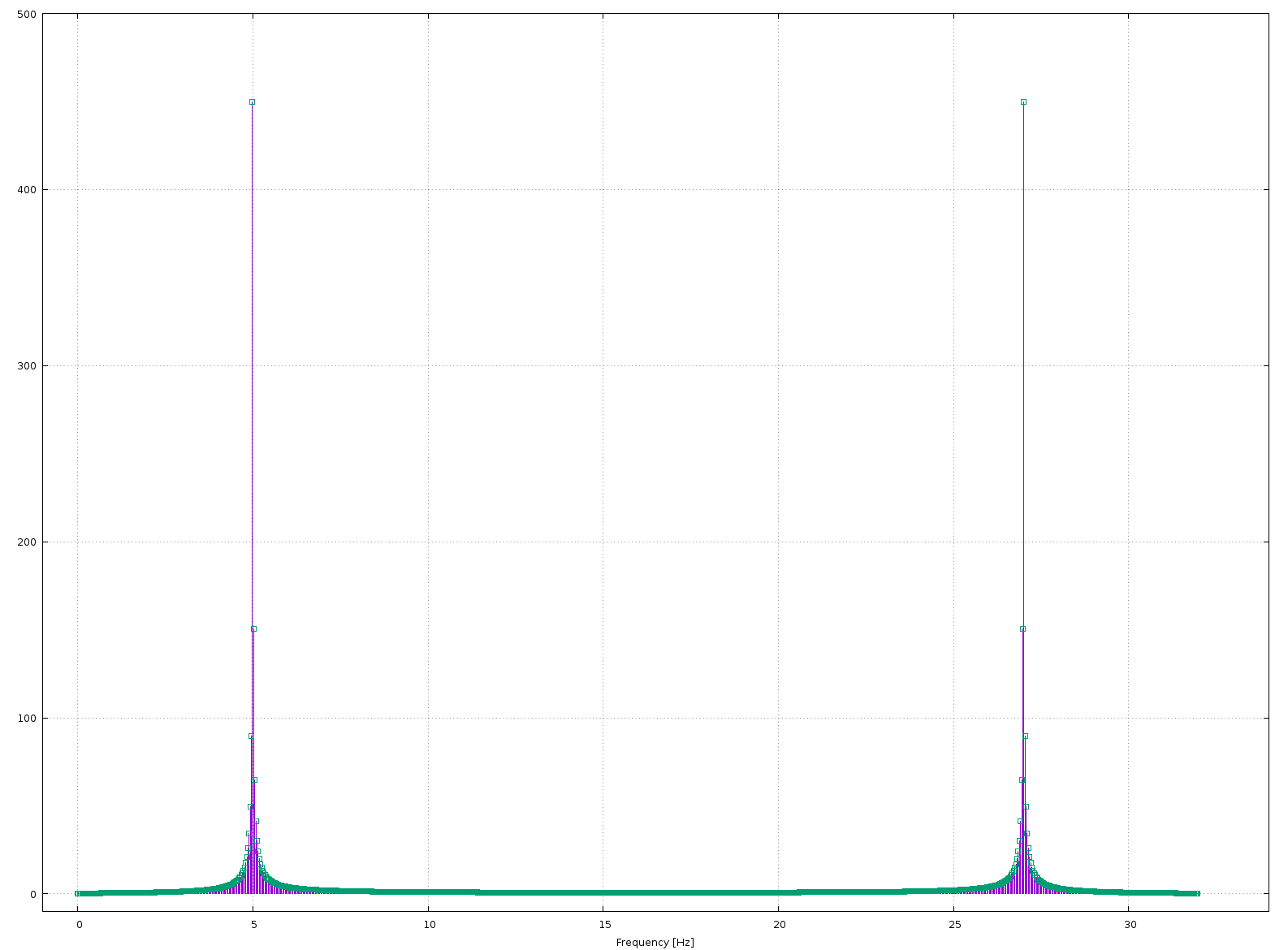
should be something like k * SampleRate/N where N is the number of points and -N/2 <=k < N/2. One has to check whether N is even/odd. Also depending on implementation the frequencies can be stored -fmax to fmax or 0 to fmax then -fmax to 0, wich means data needs to be reorganized before plotting. I am aware that this is a C++ question, but you might have a look at the documentation of pythons numpy.fft and the implementation of numpy.fft.fftfreq – Kyla

@Kyla Thanks for the comment. I'm actually coming from python and trying to reproduce the results in C++.. I'm having some trouble understanding what in the above context SampleRate exactly would be.. Can you maybe explain that? – Siegel

Does this help? https://mcmap.net/q/1777478/-eigen-fft-library – Glasper

Well, in general your FFT just knows the number of points of your signal. The answer is, hence, in units of the total interval. If you want to map this to real values you need to know the time between two points. This is often expresses in the form of "number of points per second", which is the sampling rate. The inverse is the time between two points and this is what is used in the implementation in numpy. – Kyla

@JerryJeremiah Not really, it shows how to perform the FFT correctly, but not how to obtain the frequencies either. – Siegel

@Sito: take into account that your sine is very low frequency compared to Ts. Maybe try another Ts to get the spikes more towards the center... Ts = 10/(2*pi) seems reasonable to me. As you have it now, the spike should be in the first bin: it seems ok to me. – Keratoid

@Sito: There are two spikes because Eigen returns a double-spectrum (symmetrical if the signal was real). – Keratoid

Answer 1

From your computation of time(u) I would say your sampling period Ts is 2*pi/1000 [s] which leads to Fs = 1/Ts = 1000/(2*pi) [Hz]. The analog frequency f0 of the sine you compute would be

1*t = 2*pi*f0*t [radians]
f0 = 1/(2*pi) [Hz]

Note that Fs >> f0.

On the digital domain, frequency always spans 2*pi [radians] (it could be [-pi,pi) or [0,2*pi), BUT Eigen return the latter). So you need to divide the range [0,2*pi) in N bins consistently. For example, if index is k, the associated normalized frequency is f=2*pi*k/N [radians].

To know which analog frequency f corresponds to each normalized frequency bin, compute f = (fs*k/N) [Hz], where fs is the sampling frequency.

About the scaling and the full-spectrum feature of Eigen FFT doc:

1) Scaling: Other libraries (FFTW,IMKL,KISSFFT) do not perform scaling, so there is a constant gain incurred after the forward&inverse transforms , so IFFT(FFT(x)) = Kx; this is done to avoid a vector-by-value multiply. The downside is that algorithms that worked correctly in Matlab/octave don't behave the same way once implemented in C++. How Eigen/FFT differs: invertible scaling is performed so IFFT( FFT(x) ) = x.

2) Real FFT half-spectrum: Other libraries use only half the frequency spectrum (plus one extra sample for the Nyquist bin) for a real FFT, the other half is the conjugate-symmetric of the first half. This saves them a copy and some memory. The downside is the caller needs to have special logic for the number of bins in complex vs real. How Eigen/FFT differs: The full spectrum is returned from the forward transform. This facilitates generic template programming by obviating separate specializations for real vs complex. On the inverse transform, only half the spectrum is actually used if the output type is real.

So, you should expect a gain, just make the test ifft(fft(x)) == x (tested as "error power" << "signal power"). You can divide by N to get a normalized version.

On the other hand, the two spikes you see is because of point 2. The plots you post above are only one side of the transform, the other side is symmetric if the signal is real. You can drop the high half of the output.

---

This code:

#include <eigen/Eigen/Dense>
#include <eigen/unsupported/Eigen/FFT>
#include <complex>
#include <cmath>
#include <iostream>
#include <fstream>

unsigned const N = 1000;  //
double const Fs  = 32;    // [Hz]
double const Ts  = 1./Fs; // [s] 
const double f0  = 5;     // [Hz]
std::complex<double> f(std::complex<double> const & t){
    return std::sin(2*M_PI*f0*t);
}

int main(){
    std::ofstream xrec("xrec.txt");
    Eigen::VectorXcd time(N);
    Eigen::VectorXcd f_values(N);
    Eigen::VectorXd freq(N);
    for(int u = 0; u < N; ++u){
        time(u) = u * Ts;
        f_values(u) = f(time(u));
        freq(u) = Fs * u / double(N);
    }

    Eigen::FFT<double> fft;
    Eigen::VectorXcd f_freq(N);
    fft.fwd(f_freq, f_values);

    for(int u = 0; u < N; ++u){
        xrec << freq(u) << " " << std::abs(f_freq(u)) << "\n"; 
    }
}

generates xrec.txt. Then, you can use this gnuplot script to generate a figure:

set key off
set grid
set output "figure.png"
set xlabel "Frequency [Hz]"
plot [-1:34] [-10:500] "xrec.txt" with impulses, "xrec.txt" with points pt 4

In the figure you can see two spikes at 5 and 27 Hz, as expected from this code. I changed the values to better see what is happening, just try any other ones.

In the style of the plots you show, the x-axis ranges [0,16) instead of [0,32) as in this plot, but, since your signal is real, the spectrum is symmetric and you can drop half of it .

Keratoid

I edited my question with an implementation of you suggested computation and plotted the result.. This seems quite odd, there are two spikes and the scaling of this seems a bit weird compared to the picture I'm trying to reproduce... – Siegel

Answer 2

Usually the libraries compute the DFT with the formula:

X[k] = sum_n(x[n] * exp(-2*pi * i * k * n/N)

where

• X - is the fourier domain array. The values represent the amplitude of the corresponding sine/cosine function.
• k - is the index in the fourier domain, which also uniquely define the frequency
• i - it's just the mathematical i - the complex number ( 0+1i )
• N - is the size of your array

so, at index k your frequency has length of 1/k of your whole signal input. In particular:

• X[0] is your average value
• X[1] corresponds to the sine/cosine function that fits exactly once over your whole domain
• X[2] corresponds to the sine/cosine function that fits twice over your domain ... and so on...

At indices k>N/2 the frequency is so high, that it actually corresponds to lower frequencies due to aliasing.

Here is an example for N=8:

I didn't check particularly with Eigen, but I don't think it is any different.

Anamorphosis

Isn't the FastFourierTransformation something different than the DiscretFourierTransformation? Does you anwer make sense in both contexts? B.c. I'm pretty sure the algo used in my example is the FFT and not the DFT.. – Siegel

Discrete Fourier Transform is a mathematical operation. It explains the relation between output and input but does not say how to compute it efficiently. Fast Fourier Transform is an algorithm to perform that operation. And since both input and output are digitized, we are talking about discrete and not continous FT. – Anamorphosis

First of all, thanks for the answer! Unfortunately this is not really what I'm looking for. What I need/want is an working example with Eigen's FFT algorithm and not a theoretical description. In any case, thank you for the time you invested to write this. – Siegel

I think the answer is there? freq = k where k is the column index in your f_freq matrix. – Anamorphosis