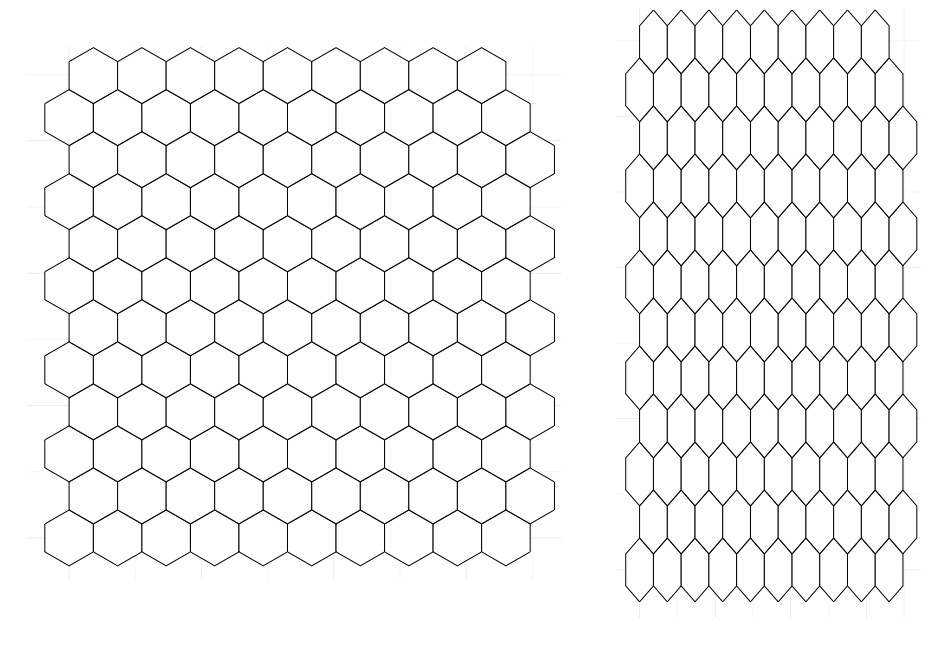
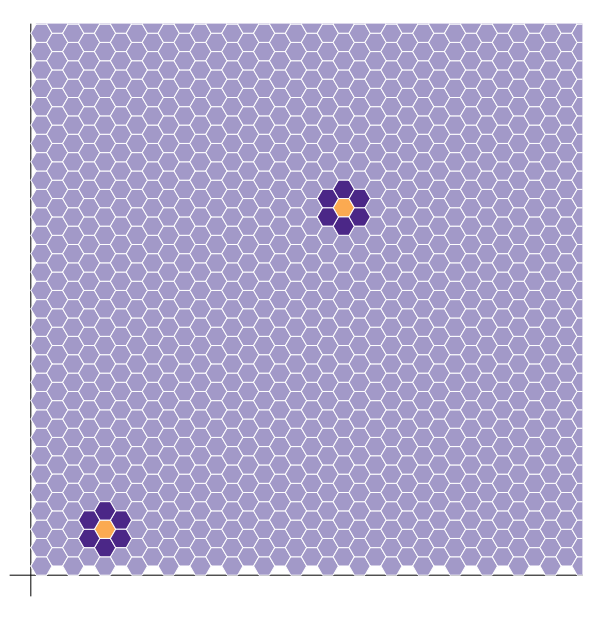
scale = 1
![enter image description here]()
scale = 2
![enter image description here]()
I wrote a hexagon() function that is a base graphics::polygon() approach. Just had to figure out a little bit of the geometry of hexagons and map it to an indexing that made sense. This is what I came up with:
The index_i = 1, index_j=1 hexagon is the lower left hexagon. It has its leftmost vertex at cartesian coordinate (0,opp). It will be flush on the y=0 line (x-axis).
The index_i = 2, index_j=1 hexagon will be adjacent to the right from the index_i = 1, index_j=1 hexagon (lower left). It'll be slightly elevated.
The index_i=1, index_j=2 will be right on top of the index_i = 1, index_j=1 hexagon (lower left).
In this way incrementing index_i references hexagons to the right (think of index_i as the x-coordinate position) and incrementing index_j references hexagons above (think of index_j as the y-coordinate position).
scale makes them bigger or smaller
pass colors to each hexagon with fill_color
Use a double for-loop to tessellate
library(RColorBrewer)
mypalette<-brewer.pal(5,"PuOr")[c(-1,-3)]
lwd.in<-1
hexagon<-function(index_i=1, index_j=1, scale=1, fill_color=sample(rev(mypalette)[2],1)){
opp=tan(pi/3)*scale;
adj=1*scale;
side_length <- sqrt(adj^2+opp^2)
vertex_a <- c( 0 , opp)
vertex_b <- c(adj , 2*opp)
vertex_c <- c(adj+side_length , 2*opp)
vertex_d <- c(adj+adj+side_length, opp)
vertex_e <- c( adj+side_length , 0)
vertex_f <- c(adj , 0)
cpoint <- c(adj+0.5*side_length,opp)
if( index_i %% 2 == 1){
odds_up_to_index_i <- seq(1,index_i,by=2)
key <- data.frame( i = seq(from=0, by=3, length.out = length(odds_up_to_index_i)),
index_i = odds_up_to_index_i)
i <- key$i[key$index_i == index_i]
j <- 2*(index_j - 1)
return_hex <-
polygon(x = c(vertex_a[1],vertex_b[1],vertex_c[1],vertex_d[1],vertex_e[1],vertex_f[1]) + cpoint[1]*i,
y = c(vertex_a[2],vertex_b[2],vertex_c[2],vertex_d[2],vertex_e[2],vertex_f[2]) + cpoint[2]*j,
col=fill_color,
lwd=lwd.in,
border=sample(c("white","black")[1],1)
)
}
if( index_i %% 2 == 0){
i <- index_i - 1
j <- 2*(index_j - 1)
return_hex <-
polygon(x = c(vertex_a[1],vertex_b[1],vertex_c[1],vertex_d[1],vertex_e[1],vertex_f[1]) + (cpoint[1]+0.5*side_length)*(i),
y = c(vertex_a[2],vertex_b[2],vertex_c[2],vertex_d[2],vertex_e[2],vertex_f[2]) + cpoint[2]*(j+1),
col=fill_color,
lwd=lwd.in,
border=sample(c("white","black")[1],1)
)
}
}
par(pty="s", mai=c(0,0,0,0)+0.1)
plot(NA,NA,xlim=c(0,200),ylim=c(0,200), axes = FALSE, xlab="", ylab="") ## if you adjust `opp` and `adj` from (7,4)
#box()
abline(v=0)
abline(h=0)
for(i in 1:100){
for(j in 1:100){
hexagon(index_i = i, index_j = j)
}
}
hexagon(index_i = 1, index_j = 1)
hexagon(index_i = 1, index_j = 2)
hexagon(index_i = 1, index_j = 3)
hexagon(index_i = 1, index_j = 4)
hexagon(index_i = 1, index_j = 5)
hexagon(index_i = 2, index_j = 1)
hexagon(index_i = 2, index_j = 2)
hexagon(index_i = 2, index_j = 3)
hexagon(index_i = 2, index_j = 4)
hexagon(index_i = 2, index_j = 5)
hexagon(index_i = 3, index_j = 1)
hexagon(index_i = 3, index_j = 2)
hexagon(index_i = 3, index_j = 3)
hexagon(index_i = 3, index_j = 4)
hexagon(index_i = 3, index_j = 5)
hexagon(index_i = 4, index_j = 1)
hexagon(index_i = 4, index_j = 2)
hexagon(index_i = 4, index_j = 3)
hexagon(index_i = 4, index_j = 4)
hexagon(index_i = 4, index_j = 5)
hexagon(index_i = 5, index_j = 1)
hexagon(index_i = 5, index_j = 5)
hexagon(index_i = 6, index_j = 1)
hexagon(index_i = 6, index_j = 4)
hexagon(index_i = 7, index_j = 2)
hexagon(index_i = 7, index_j = 3)
hexagon(index_i = 7, index_j = 4)
## Infected: color, white border
hexagon(index_i = 5, index_j = 3, fill_color=rev(mypalette)[3])
## Vaccinated: deeper color, black border (nah, just white)
hexagon(index_i = 5, index_j = 2, fill_color=rev(mypalette)[1])
hexagon(index_i = 6, index_j = 3, fill_color=rev(mypalette)[1])
hexagon(index_i = 6, index_j = 2, fill_color=rev(mypalette)[1])
hexagon(index_i = 5, index_j = 4, fill_color=rev(mypalette)[1])
hexagon(index_i = 4, index_j = 2, fill_color=rev(mypalette)[1])
hexagon(index_i = 4, index_j = 3, fill_color=rev(mypalette)[1])
## Infected: color, white border
hexagon(index_i = 20, index_j = 20, fill_color=rev(mypalette)[3])
## Vaccinated: deeper color, black border (nah, just white)
hexagon(index_i = 20, index_j = 19, fill_color=rev(mypalette)[1])
hexagon(index_i = 20, index_j = 21, fill_color=rev(mypalette)[1])
hexagon(index_i = 19, index_j = 20, fill_color=rev(mypalette)[1])
hexagon(index_i = 19, index_j = 21, fill_color=rev(mypalette)[1])
hexagon(index_i = 21, index_j = 20, fill_color=rev(mypalette)[1])
hexagon(index_i = 21, index_j = 21, fill_color=rev(mypalette)[1])
par(pty="s", mai=c(0,0,0,0)+0.1)
plot(NA,NA,xlim=c(0,200),ylim=c(0,200), axes = FALSE, xlab="", ylab="") ## if you adjust `opp` and `adj` from (7,4)
#box()
abline(v=0)
abline(h=0)
scale.in <- 2
for(i in 1:100){
for(j in 1:100){
hexagon(index_i = i, index_j = j, scale=scale.in)
}
}
hexagon(index_i = 1, index_j = 1, scale=scale.in)
hexagon(index_i = 1, index_j = 2, scale=scale.in)
hexagon(index_i = 1, index_j = 3, scale=scale.in)
hexagon(index_i = 1, index_j = 4, scale=scale.in)
hexagon(index_i = 1, index_j = 5, scale=scale.in)
hexagon(index_i = 2, index_j = 1, scale=scale.in)
hexagon(index_i = 2, index_j = 2, scale=scale.in)
hexagon(index_i = 2, index_j = 3, scale=scale.in)
hexagon(index_i = 2, index_j = 4, scale=scale.in)
hexagon(index_i = 2, index_j = 5, scale=scale.in)
hexagon(index_i = 3, index_j = 1, scale=scale.in)
hexagon(index_i = 3, index_j = 2, scale=scale.in)
hexagon(index_i = 3, index_j = 3, scale=scale.in)
hexagon(index_i = 3, index_j = 4, scale=scale.in)
hexagon(index_i = 3, index_j = 5, scale=scale.in)
hexagon(index_i = 4, index_j = 1, scale=scale.in)
hexagon(index_i = 4, index_j = 2, scale=scale.in)
hexagon(index_i = 4, index_j = 3, scale=scale.in)
hexagon(index_i = 4, index_j = 4, scale=scale.in)
hexagon(index_i = 4, index_j = 5, scale=scale.in)
hexagon(index_i = 5, index_j = 1, scale=scale.in)
hexagon(index_i = 5, index_j = 5, scale=scale.in)
hexagon(index_i = 6, index_j = 1, scale=scale.in)
hexagon(index_i = 6, index_j = 4, scale=scale.in)
hexagon(index_i = 7, index_j = 2, scale=scale.in)
hexagon(index_i = 7, index_j = 3, scale=scale.in)
hexagon(index_i = 7, index_j = 4, scale=scale.in)
## Infected: color, white border
hexagon(index_i = 5, index_j = 3, scale=scale.in, fill_color=rev(mypalette)[3])
## Vaccinated: deeper color, black border (nah, just white)
hexagon(index_i = 5, index_j = 2, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 6, index_j = 3, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 6, index_j = 2, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 5, index_j = 4, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 4, index_j = 2, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 4, index_j = 3, scale=scale.in, fill_color=rev(mypalette)[1])
## Infected: color, white border
hexagon(index_i = 20, index_j = 20, scale=scale.in, fill_color=rev(mypalette)[3])
## Vaccinated: deeper color, black border (nah, just white)
hexagon(index_i = 20, index_j = 19, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 20, index_j = 21, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 19, index_j = 20, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 19, index_j = 21, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 21, index_j = 20, scale=scale.in, fill_color=rev(mypalette)[1])
hexagon(index_i = 21, index_j = 21, scale=scale.in, fill_color=rev(mypalette)[1])