After playing around with some ideas, I came up with another solution, more accurate and probably faster, if done correctly, than that of my previous answer. It is however quite complicated and requires quite a bit of maths, although not very complex maths. Moreover, this is a work in progress: I am still investigating some areas. Nonetheless, from what I've tried, it does already produce very good results.
The problem
Definitions and goal
Throughout this answer, p[n] refers to the position of the nth point, v[n] to its velocity, a[n] to its acceleration, and j[n] to its jerk (the derivative of acceleration). The velocity of the nth point depends only on its position and that of the previous point. Similarly for acceleration and jerk, but with the points velocity and acceleration, respectively.
We have a start point and an end point, respectively p[0] and p[n], both with associated velocities v[0] and v[n]. The goal is to place n-1 points in between, with an arbitrary n, such that, along the X, Y, and Z axes, the absolute values of acceleration and jerk at any of these points (and at p[n]) are below some limits, respectively aMaxX, aMaxY, and aMaxZ for acceleration, and jMaxX, jMaxY, and jMaxZ for jerk.
What we want to find is the values of p[i] for all i ∈ [1; n-1]. Because p[i] = p[i-1] + v[i], this is the same as finding v[i]. By the same reasoning, with v[i] = v[i-1] + a[i] and a[i] = a[i-1] + j[i], it is also the same as finding a[i] or j[i].
a[0] and a[n+1] are assumed to be zero.
Observations and simplifications
Because the problem's constraints are independant of the dimension, we can solve for each of the three dimensions separately, as long as the number of points obtained in each case is the same. Therefore, I am only going to solve the one-dimensional version of the problem, using aMax and jMax, irrespective of the axis.
*[WIP]* Determine the worst case to solve first, then solve the other ones, knowing the number of points.
The actual positions of the two given points are irrelevant, what matters is the relative distance between them, which we can define as P = p[n] - p[0]. Let's also define the ranges R = [1; n] and R* = [1; n+1].
Because of the discrete nature of the problem, we can obtain the following equations. Note that ∑{i∈R}(x[i]) is the sum of all x[i] for i∈R.
Ⓐ ∑{i∈R}(v[i]) = P
Ⓑ ∑{i∈R}(a[i]) = v[n] - v[0]
Ⓧ ∑{i∈R*}(j[i]) = 0
Ⓧ comes from the assumption that a[0] = a[n+1] = 0.
From Ⓐ and v[i] = v[i-1] + a[i], i∈R, we can deduce:
Ⓒ ∑{i∈R}((n+1-i)*a[i]) = P - n*v[0]
By the same logic, from Ⓑ, Ⓒ, and a[i] = a[i-1] + j[i], i∈R, we can deduce:
Ⓨ ∑{i∈R}((n+1-i)*j[i]) = v[n] - v[0]
Ⓩ ∑{i∈R}(T[n+1-i]*j[i]) = P - n*v[0]
Here, T[n] is the nth triangular number, defined by T[n] = n*(n+1)/2.
The equations Ⓧ, Ⓨ, and Ⓩ are the relevant ones for the next parts.
The approach
In order to minimize n, we can start with a small value of n (1, 2?) and find a solution. Then, if max{i∈R}(abs(a[i])) > aMax or max{i∈R}(abs(j[i])) > jMax, we can increment n and repeat the process.
*[WIP]* Find a lower bound for n to avoid unnecessary calculations from small values of n. Or estimate the correct value of n and pinpoint it by testing solutions.
Finding a solution requires finding the values of j[i] for all i∈R*. I have yet to find an optimal form for j[i], but defining j*[i], r[i] and s[i] such that
j[i] = j*[i] + r[i]v[0] + s[i]v[n]
works quite well.
*[WIP]* Find a better form for j[i]
By doing that, we transform our n-1 unknowns (j[i], i∈R, note that j[n+1] = -∑{i∈R}(j[i])) into 3(n-1) easier to find unknowns. Here are a few things we can deduce right now from Ⓧ, Ⓨ, and Ⓩ.
∑{i∈R*}(r[i]) = 0
∑{i∈R*}(s[i]) = 0
∑{i∈R}((n+1-i)*r[i]) = -1
∑{i∈R}((n+1-i)*s[i]) = 1
∑{i∈R}(T(n+1-i)*r[i]) = -n
∑{i∈R}(T(n+1-i)*s[i]) = 0
As a reminder, here are Ⓧ, Ⓨ, and Ⓩ.
Ⓧ ∑{i∈R*}(j[i]) + j[n+1] = 0
Ⓨ ∑{i∈R}((n+1-i)*j[i]) = v[n] - v[0]
Ⓩ ∑{i∈R}(T[n+1-i]*j[i]) = P - n*v[0]
The goal now is to find adequate special cases to help us determine these unknowns.
The special cases
v[0] = v[n] = 0
By playing with values of jerk, I observed that taking all of j[i], i∈R* as part of a parabola yields excellent results for minimizing both jerk and acceleration. Although it isn't the best possible fit, I haven't found better yet.
The intuition behind values of jerk coming from a parabola is that, if the values of position are to follow a polynomial, then its degree must be at least 5, and can be 5. This is easier to understand if you think about the values of velocity following a 4th degree polynomial. The constraints that v[0] and v[n] are set, a[0] = a[n+1] = 0, and that its integral over [0; n] must equal P, this polynomial must have a degree of at least 4. This holds for both continuous and dicrete cases. Finally, it seems that taking the smallest degree leads to a smoother jerk as well as making it easier to calculate.
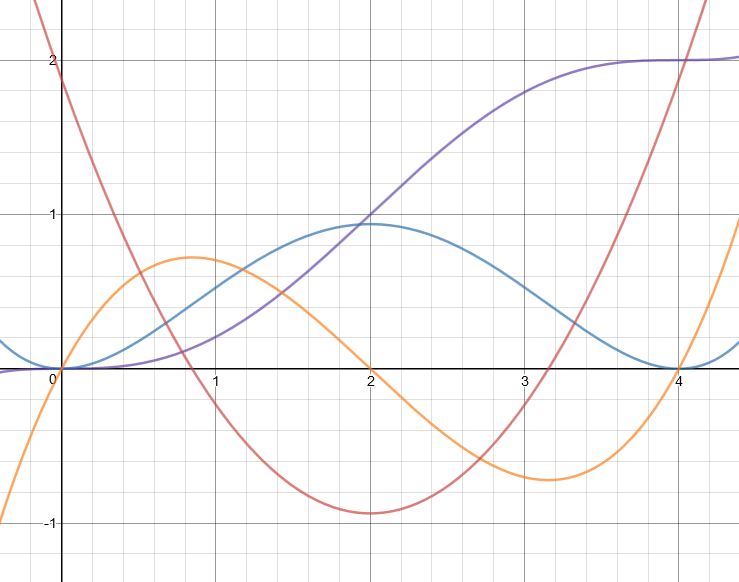
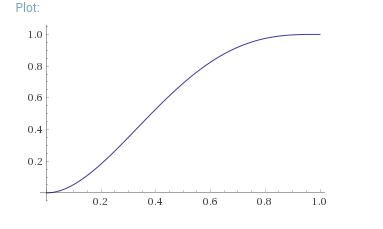
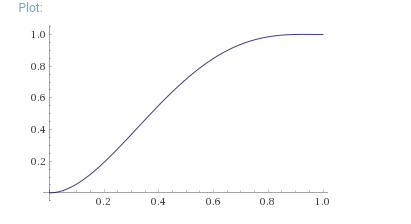
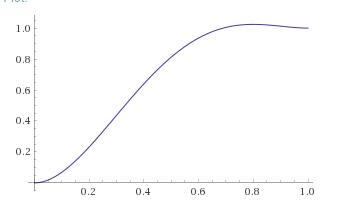
Here is an example of a continuous case where the position is in purple, the velocity in blue, the acceleration in yellow and the jerk in red.
![Example curves for position, velocity, acceleration, and jerk]()
In case you want to play with this, here is how to define the position curve in terms of n, p[0], p[n], v[0], and v[n] (the other ones are simply derivatives).
a = (-3(v[n]+v[0]) + 6(p[n]-p[0])) / n^5
b = (n(7v[n]+8v[0]) - 15(p[n]-p[0])) / n^4
c = (-n(4v[n]+6v[0]) + 10(p[n]-p[0])) / n^3
p[x] = ax^5 + bx^4 + cx^3 + v[0]x + p[0]
If v[0] = v[n] = 0, then j[i] = j*[i], i∈R*. That means that the values j*[i] follow a quadratic polynomial. So we want to find α, β, and γ such that Ⓟ holds.
Ⓟ j*[i] = αi^2 + βi + γ, i∈R*
From Ⓧ, Ⓨ, and Ⓩ follow these equations.
α*∑{i∈R*}(i^2) + β*∑{i∈R*}(i) + c*∑{i∈R*}(1) = 0
α*∑{i∈R}((n+1-i)*i^2) + β*∑{i∈R}((n+1-i)*i) + c*∑{i∈R}(n+1-i) = 0
α*∑{i∈R}(T(n+1-i)*i^2) + β*∑{i∈R}(T(n+1-i)*i) + c*∑{i∈R}(T(n+1-i)) = P
Solving this system gives α, β, and γ, which can be used with Ⓟ to calculate j*[i], i∈R*. Note that j*[i] = j*[n+2-i], so only the upper half of the calculations need to be done.
v[0] = v[n] = 1/n
If v[0] = v[n] = 1/n, then j[i] = 0, i∈R*. This means that Ⓠ holds.
Ⓠ r[i] + s[i] = -n*j[i], i∈R*
v[0] = 0, j[i∈L] = J, j[h] = 0, j[i∈U] = -J
L and U are respectively the lower and upper halves of R*, and h is the value in between, if n+1 is odd. In other words:
if n is odd:
L = [1; (n+1)/2]
U = [(n+3)/2; n+1]
if n is even:
L = [1; n/2]
h = n/2+1
U = [n/2+2; n]
This special case corresponds to the maximum overall acceleration between p[0] and p[n] while minimizing abs(j[i]), i∈R*. Here, Ⓩ gives us the following equation.
∑{i∈R}(T[n+1-i]*j[i]) = P
∑{i∈L}(T[n+1-i])*j[1] + ∑{i∈U}(T[n+1-i])*j[n+1] = P
j[1] = P / [ ∑{i∈L}(T[n+1-i]) - ∑{i∈U}(T[n+1-i]) ]
This gives j[1], and so every j[i], i∈R*. We can then calculate v[n] using Ⓨ.
Putting the pieces together
Each special case gives us, for some values of v[0], v[n] and P, a relation of the form
αj*[i] + βr[i] + γs[i] = δ.
By treating three special cases (assuming they are not similar, meaning the do not give the same relation), we have a system of three equations that, once solved, gives the values of j*[i], r[i] and s[i] for all i∈R*.
As a result, we can calculate, for each value of n, values of j[i] depending on v[0], v[n] and P. They can be precalculated, which means testing them for any value of n can be very fast. Thereby, we can very quicklyt find a good estimate for the fewest amount of points needed in the trajectory, as well as a good approximation of the best trajectory possible, as long as we have precalculated values up to a sufficiently large value of n.

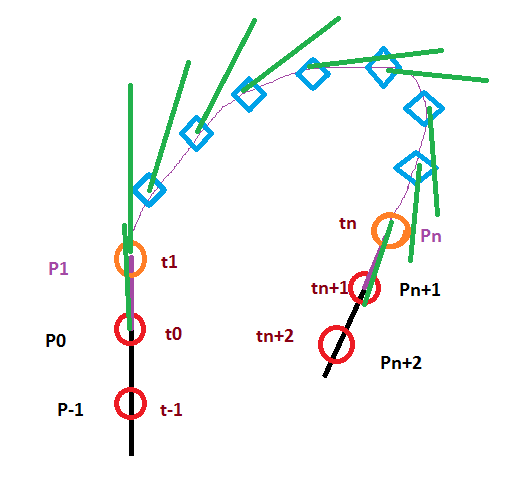

Pn? – FransenV0 = P0 - P-1orV0 = P1 - P0? Does the velocity at some point lead you to the next point, or from the previous one to the current one? – QuinlanP0andV0and you want to get toPfinalandVfinalin the minimum amount of time? – Landmeier