Cubic hermit spline interpolation python

Question

I would like to calculate a third-degree polynomial that is defined by its function values and derivatives at specified points.

https://en.wikipedia.org/wiki/Cubic_Hermite_spline

I know of scipy's interpolation methods. Specifically

splprep to interpolate a N-dimensional spline and splev to eveluate its derivatives.

Is there a python routine that takes function values f(x) and derivatives f'(x) corresponding to values x and calculates a spline representation that fits the given data.

To give an example:
I have two object positions in space defined by the coordinates x,y,z and I know the velocity x',y',z' of the object at these positions. Can I now interpolate the path that the object takes between the two points over time t. Taking all the given parameters into account.

Excitor

Answer 1

You can use BPoly.from_derivatives. The result is a polynomial in the Bernstein basis.

Longueur

Answer 2

Extending ev-br's answer, here some sample code that exemplifies the usage of BPoly.from_derivatives to interpolate between points in n dimensions with prescribed derivatives.

import numpy as np
from scipy import interpolate

def sampleCubicSplinesWithDerivative(points, tangents, resolution):
    '''
    Compute and sample the cubic splines for a set of input points with
    optional information about the tangent (direction AND magnitude). The 
    splines are parametrized along the traverse line (piecewise linear), with
    the resolution being the step size of the parametrization parameter.
    The resulting samples have NOT an equidistant spacing.

    Arguments:      points: a list of n-dimensional points
                    tangents: a list of tangents
                    resolution: parametrization step size
    Returns:        samples

    Notes: Lists points and tangents must have equal length. In case a tangent
           is not specified for a point, just pass None. For example:
                    points = [[0,0], [1,1], [2,0]]
                    tangents = [[1,1], None, [1,-1]]

    '''
    resolution = float(resolution)
    points = np.asarray(points)
    nPoints, dim = points.shape

    # Parametrization parameter s.
    dp = np.diff(points, axis=0)                 # difference between points
    dp = np.linalg.norm(dp, axis=1)              # distance between points
    d = np.cumsum(dp)                            # cumsum along the segments
    d = np.hstack([[0],d])                       # add distance from first point
    l = d[-1]                                    # length of point sequence
    nSamples = int(l/resolution)                 # number of samples
    s,r = np.linspace(0,l,nSamples,retstep=True) # sample parameter and step

    # Bring points and (optional) tangent information into correct format.
    assert(len(points) == len(tangents))
    data = np.empty([nPoints, dim], dtype=object)
    for i,p in enumerate(points):
        t = tangents[i]
        # Either tangent is None or has the same
        # number of dimensions as the point p.
        assert(t is None or len(t)==dim)
        fuse = list(zip(p,t) if t is not None else zip(p,))
        data[i,:] = fuse

    # Compute splines per dimension separately.
    samples = np.zeros([nSamples, dim])
    for i in range(dim):
        poly = interpolate.BPoly.from_derivatives(d, data[:,i])
        samples[:,i] = poly(s)
    return samples

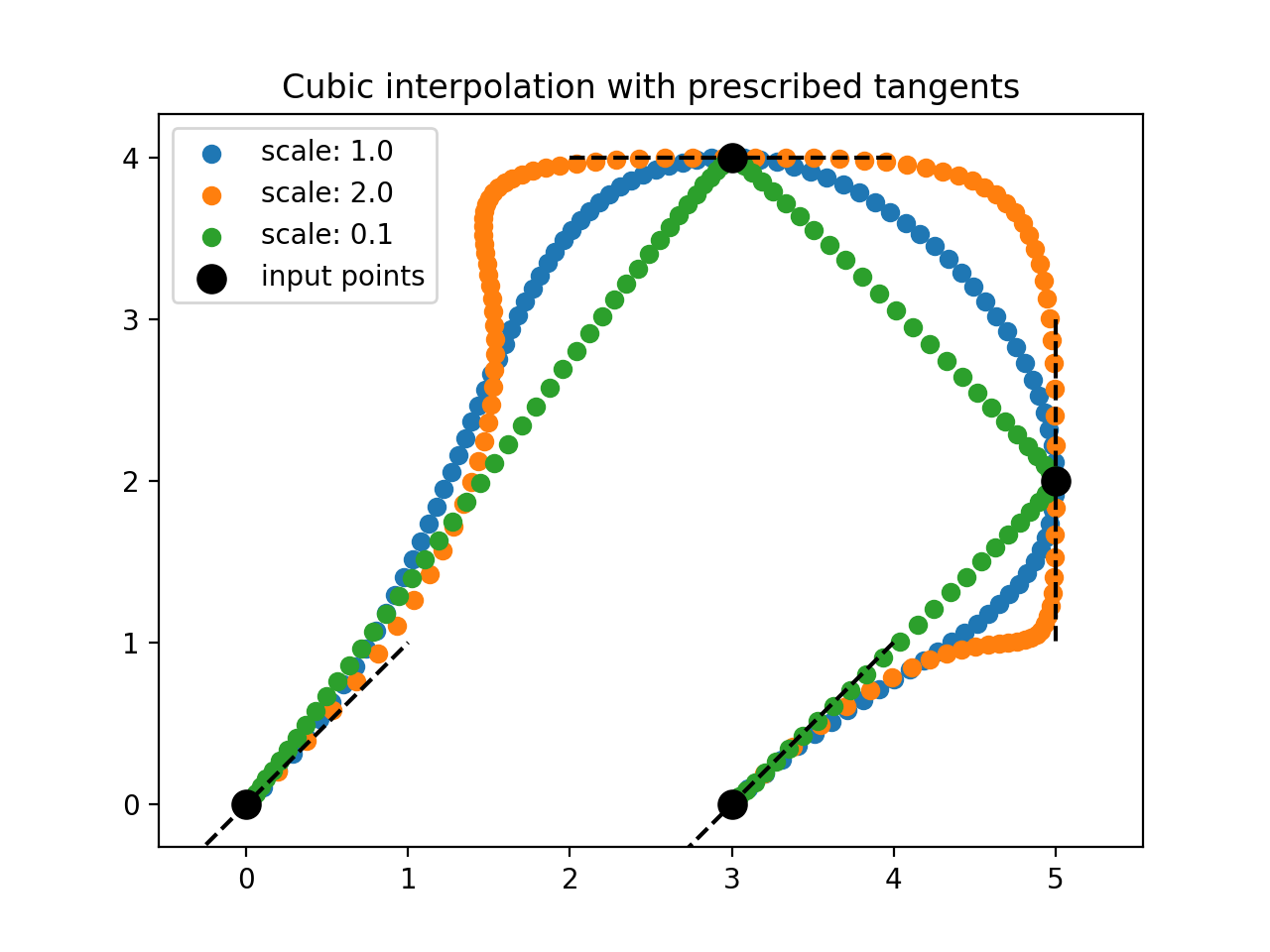
To demonstrate the use of this function, we specify the points and tangents. The example further demonstrates the effect if the "magnitude" of the tangents is changed.

# Input.
points = []
tangents = []
resolution = 0.2
points.append([0.,0.]); tangents.append([1,1])
points.append([3.,4.]); tangents.append([1,0])
points.append([5.,2.]); tangents.append([0,-1])
points.append([3.,0.]); tangents.append([-1,-1])
points = np.asarray(points)
tangents = np.asarray(tangents)

# Interpolate with different tangent lengths, but equal direction.
scale = 1.
tangents1 = np.dot(tangents, scale*np.eye(2))
samples1 = sampleCubicSplinesWithDerivative(points, tangents1, resolution)
scale = 2.
tangents2 = np.dot(tangents, scale*np.eye(2))
samples2 = sampleCubicSplinesWithDerivative(points, tangents2, resolution)
scale = 0.1
tangents3 = np.dot(tangents, scale*np.eye(2))
samples3 = sampleCubicSplinesWithDerivative(points, tangents3, resolution)

# Plot.
import matplotlib.pyplot as plt
plt.scatter(samples1[:,0], samples1[:,1], marker='o', label='samples1')
plt.scatter(samples2[:,0], samples2[:,1], marker='o', label='samples2')
plt.scatter(samples3[:,0], samples3[:,1], marker='o', label='samples3')
plt.scatter(points[:,0], points[:,1], s=100, c='k', label='input')
plt.axis('equal')
plt.title('Interpolation')
plt.legend()
plt.show()

This results in the following plot:

Three things to note:

• The following can also be applied for more than two dimensions.
• The spacing between the samples is not fixed. One simple way to achieve equidistant sampling is to interpolate linearly between the returned samples, as it has been discussed for instance in this post.
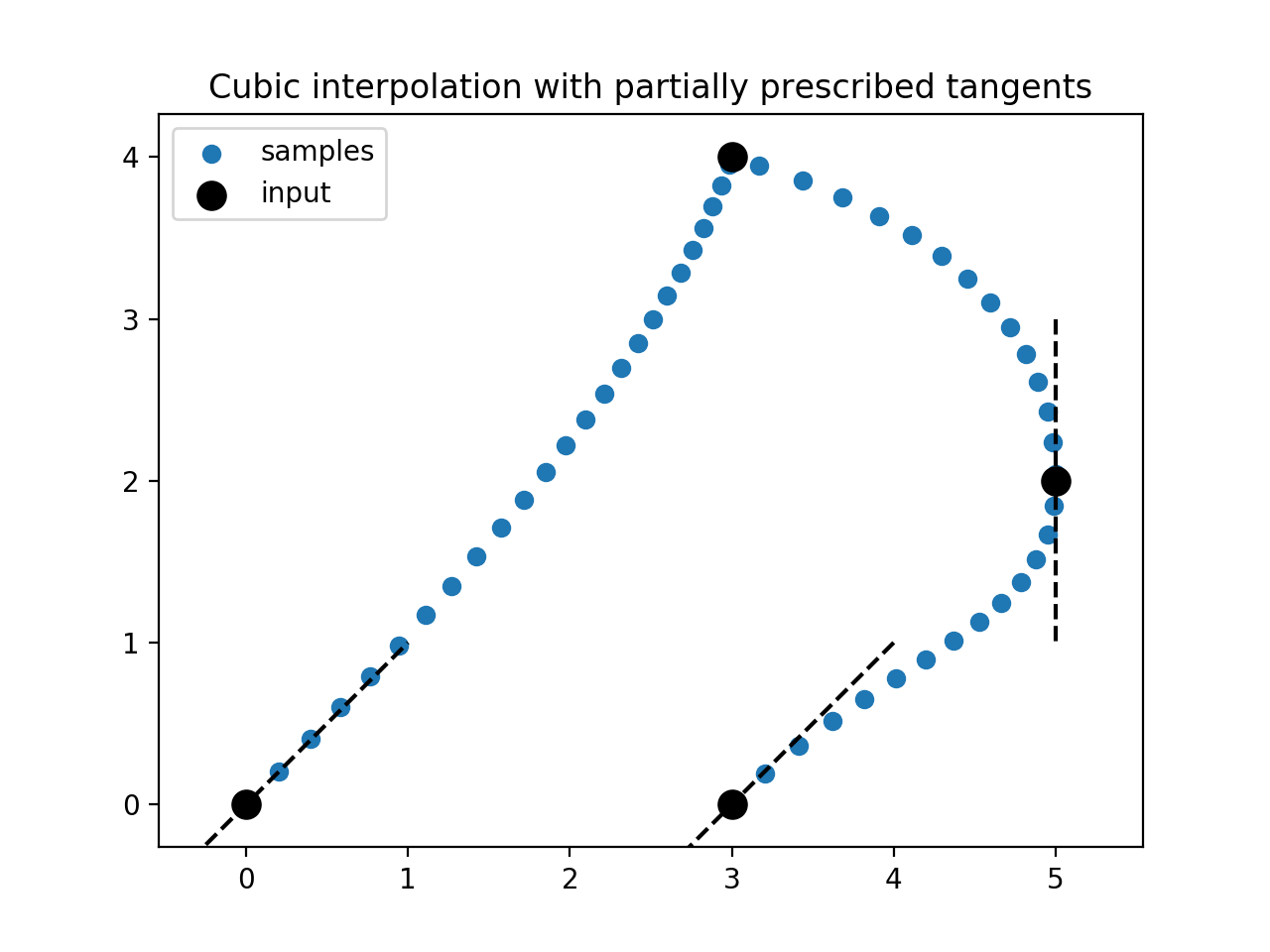
• The specification of the tangents is optional, however BPoly.from_derivatives does not ensure smooth transitions between the splines at this position. If for example tangents[1] in the above sample is set to None, sampleCubicSplinesWithDerivative(points, tangents, resolution), the result will look like this:

Beetlebrowed