How to generate equispaced interpolating values

Question

I have a list of (x,y) values that are not uniformly spaced. Here is the archive used in this question.

I am able to interpolate between the values but what I get are not equispaced interpolating points. Here's what I do:

x_data = [0.613,0.615,0.615,...]
y_data = [5.919,5.349,5.413,...]

# Interpolate values for x and y.
t = np.linspace(0, 1, len(x_data))
t2 = np.linspace(0, 1, 100)
# One-dimensional linear interpolation.
x2 = np.interp(t2, t, x_data)
y2 = np.interp(t2, t, y_data)

# Plot x,y data.
plt.scatter(x_data, y_data, marker='o', color='k', s=40, lw=0.)

# Plot interpolated points.
plt.scatter(x2, y2, marker='o', color='r', s=10, lw=0.5)

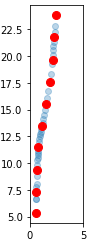
Which results in:

As can be seen, the red dots are closer together in sections of the graph where the original points distribution is denser.

I need a way to generate the interpolated points equispaced in x, y according to a given step value (say 0.1)

---

As askewchan correctly points out, when I mean "equispaced in x, y" I mean that two consecutive interpolated points in the curve should be distanced from each other (euclidean straight line distance) by the same value.

---

I tried unubtu's answer and it works well for smooth curves but seems to break for not so smooth ones:

This happens because the code calculates the point distance in an euclidean way instead of directly over the curve and I need the distance over the curve to be the same between points. Can this issue be worked around somehow?

Allium

Does "equispaced in x, y" mean equidistant along the curve's tangent? – Smithers

@Smithers sorry, I expressed myself ambiguously. I'll refactor the question to make this more clear. – Allium

In other words, you want dx = step / sqrt(1 + (y')**2) – Smithers

I'm not sure I follow you @askewchan, could you expand on your comment a bit? – Allium

You'll want to build your interpolation as a function y(x) and then call it on some array x which is not linearly spaced, but spaced with each step in x (dx) being your desired step (say ds) divided by the the sqrt of (1 + the slope squared). This is because the arclength of a segment of the curve has length ds = sqrt(1 + slope^2)*dx (from pythagorean theorem ds^2 = dx^2 + dy^2) – Smithers

"... should be distanced from each other ...", how do you measure the distance? Straight line or distance along the curve? – Falgout

@Falgout a straight line would be enough given that the points are not too far apart. I've added this to the question. – Allium

Answer 1

Let's first consider a simple case. Suppose your data looked like the blue line, below.

If you wanted to select equidistant points that were r distance apart, then there would be some critical value for r where the cusp at (1,2) is the first equidistant point.

If you wanted points that were greater than this critical distance apart, then the first equidistant point would jump from (1,2) to some place very different -- depicted by the intersection of the green arc with the blue line. The change is not gradual.

This toy case suggests that a tiny change in the parameter r can have a radical, discontinuous affect on the solution.

It also suggests that you must know the location of the ith equidistant point before you can determine the location of the (i+1)-th equidistant point.

So it appears an iterative solution is required:

import numpy as np
import matplotlib.pyplot as plt
import math

x, y = np.genfromtxt('data', unpack=True, skip_header=1)
# find lots of points on the piecewise linear curve defined by x and y
M = 1000
t = np.linspace(0, len(x), M)
x = np.interp(t, np.arange(len(x)), x)
y = np.interp(t, np.arange(len(y)), y)
tol = 1.5
i, idx = 0, [0]
while i < len(x):
    total_dist = 0
    for j in range(i+1, len(x)):
        total_dist += math.sqrt((x[j]-x[j-1])**2 + (y[j]-y[j-1])**2)
        if total_dist > tol:
            idx.append(j)
            break
    i = j+1

xn = x[idx]
yn = y[idx]
fig, ax = plt.subplots()
ax.plot(x, y, '-')
ax.scatter(xn, yn, s=50)
ax.set_aspect('equal')
plt.show()

Note: I set the aspect ratio to 'equal' to make it more apparent that the points are equidistant.

Parasite

This is a great answer, sorry I took so long to get back to you (got caught up with another issue) This code works great for reasonably smooth curves, but appears to fail for not so well behaved curves. Please see edited question. – Allium

@Gabriel: I've edited my answer. It's basically the same -- you just keep track of a running total of the distance as you hop between points. – Parasite

Thank you very much @unubtu, this answer is perfect now! – Allium

Answer 2

Convert your xy-data to a parametrized curve, i.e. calculate all all distances between the points and generate the coordinates on the curve by cumulative summing. Then interpolate the x- and y-coordinates independently with respect to the new coordinates.

import numpy as np
from matplotlib import pyplot as plt

data = '''0.615   5.349
    0.615   5.413
    0.617   6.674
    0.617   6.616
    0.63    7.418
    0.642   7.809
    0.648   8.04
    0.673   8.789
    0.695   9.45
    0.712   9.825
    0.734   10.265
    0.748   10.516
    0.764   10.782
    0.775   10.979
    0.783   11.1
    0.808   11.479
    0.849   11.951
    0.899   12.295
    0.951   12.537
    0.972   12.675
    1.038   12.937
    1.098   13.173
    1.162   13.464
    1.228   13.789
    1.294   14.126
    1.363   14.518
    1.441   14.969
    1.545   15.538
    1.64    16.071
    1.765   16.7
    1.904   17.484
    2.027   18.36
    2.123   19.235
    2.149   19.655
    2.172   20.096
    2.198   20.528
    2.221   20.945
    2.265   21.352
    2.312   21.76
    2.365   22.228
    2.401   22.836
    2.477   23.804'''

data = np.array([line.split() for line in data.split('\n')],dtype=float)

x,y = data.T
xd = np.diff(x)
yd = np.diff(y)
dist = np.sqrt(xd**2+yd**2)
u = np.cumsum(dist)
u = np.hstack([[0],u])

t = np.linspace(0,u.max(),10)
xn = np.interp(t, u, x)
yn = np.interp(t, u, y)

f = plt.figure()
ax = f.add_subplot(111)
ax.set_aspect('equal')
ax.plot(x,y,'o', alpha=0.3)
ax.plot(xn,yn,'ro', markersize=8)
ax.set_xlim(0,5)

Catalyze

In my case, it gives me ValueError: object too deep for desired array at this line - xn = numpy.interp(t, u, x) – Viridis

I just ran the code and it works fine. numpy is version 1.10.1 and scipy 0.15.1 – Catalyze

Thanks for this, this is exactly what I was also looking for. Any thoughts as to how one could adapt this to higher dimensional data (perhaps with scipy.interpolate.interpn)? I'd rather not loop over every dimension and do np.interp independently. – Cadaverous

Literally 10 minutes after this comment I found the solution :). Posted as an answer here – Cadaverous

Answer 3

The following script will interpolate points with a equal step of x_max - x_min / len(x) = 0.04438

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt

data = np.loadtxt('data.txt')
x = data[:,0]
y = data[:,1]

f = interp1d(x, y)
x_new = np.linspace(np.min(x), np.max(x), x.shape[0])
y_new = f(x_new)

plt.plot(x,y,'o', x_new, y_new, '*r')
plt.show()

Forrest

This solution generates points equispaced in x but not in y, thus not equispaced in the curve. Thank you anyway for the answer. – Allium

Answer 4

Expanding on the answer by @Christian K., here's how to do this for higher dimensional data with scipy.interpolate.interpn. Let's say we want to resample to 10 equally-spaced points:

import numpy as np
import scipy
# Assuming that 'data' is rows x dims (where dims is the dimensionality)
diffs = data[1:, :] - data[:-1, :]
dist = np.linalg.norm(diffs, axis=1)
u = np.cumsum(dist)
u = np.hstack([[0], u])
t = np.linspace(0, u[-1], 10)
resampled = scipy.interpolate.interpn((u,), pts, t)

Cadaverous

Answer 5

It IS possible to generate equidistant points along the curve. But there must be more definition of what you want for a real answer. Sorry, but the code I've written for this task is in MATLAB, but I can describe the general ideas. There are three possibilities.

First, are the points to be truly equidistant from the neighbors in terms of a simple Euclidean distance? To do so would involve finding the intersection at any point on the curve with a circle of a fixed radius. Then just step along the curve.

Next, if you intend distance to mean distance along the curve itself, if the curve is a piecewise linear one, the problem is again easy to do. Just step along the curve, since distance on a line segment is easy to measure.

Finally, if you intend for the curve to be a cubic spline, again this is not incredibly difficult, but is a bit more work. Here the trick is to:

• Compute the piecewise linear arclength from point to point along the curve. Call it t.
• Generate a pair of cubic splines, x(t), y(t).
• Differentiate x and y as functions of t. Since these are cubic segments, this is easy. The derivative functions will be piecewise quadratic.
• Use an ode solver to move along the curve, integrating the differential arclength function. In MATLAB, ODE45 worked nicely.

Thus, one integrates

sqrt((x')^2 + (y')^2)

Again, in MATLAB, ODE45 can be set to identify those locations where the function crosses certain specified points.

If your MATLAB skills are up to the task, you can look at the code in interparc for more explanation. It is reasonably well commented code.

Calv