OpenGL - Mouse coordinates to Space coordinates

Question

My goal is to place a sphere right at where the mouse is pointing (with Z-coord as 0).

I saw this question but I didn't yet understand the MVP matrices concept, so I researched a bit, and now I have two questions:

How to create a view matrix from the camera settings such as the lookup, eye and up vector?

I also read this tutorial about several camera types and this one for webgl.

I still can put it all together I don't know how to get the projection matrix also...

What steps should I do to implement all of this?

Bloodstream

Answer 1

In a rendering, each mesh of the scene usually is transformed by the model matrix, the view matrix and the projection matrix.

• Projection matrix:
  The projection matrix describes the mapping from 3D points of a scene, to 2D points of the viewport. The projection matrix transforms from view space to the clip space, and the coordinates in the clip space are transformed to the normalized device coordinates (NDC) in the range (-1, -1, -1) to (1, 1, 1) by dividing with the w component of the clip coordinates.

• View matrix:
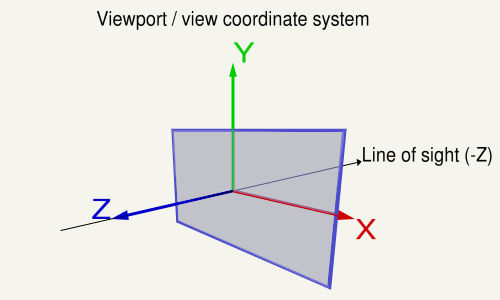
  The view matrix describes the direction and position from which the scene is looked at. The view matrix transforms from the world space to the view (eye) space. In the coordinate system on the viewport, the X-axis points to the left, the Y-axis up and the Z-axis out of the view (Note in a right hand system the Z-Axis is the cross product of the X-Axis and the Y-Axis).

• Model matrix:
  The model matrix defines the location, orientation and the relative size of an mesh in the scene. The model matrix transforms the vertex positions from of the mesh to the world space.

The model matrix looks like this:

( X-axis.x, X-axis.y, X-axis.z, 0 )
( Y-axis.x, Y-axis.y, Y-axis.z, 0 )
( Z-axis.x, Z-axis.y, Z-axis.z, 0 )
( trans.x,  trans.y,  trans.z,  1 ) 

View

On the viewport the X-axis points to the left, the Y-axis up and the Z-axis out of the view (Note in a right hand system the Z-Axis is the cross product of the X-Axis and the Y-Axis).

The code below defines a matrix that exactly encapsulates the steps necessary to calculate a look at the scene:

• Converting model coordinates into viewport coordinates.
• Rotation, to look in the direction of the view.
• Movement to the eye position

The following code does the same as gluLookAt or glm::lookAt does:

using TVec3  = std::array< float, 3 >;
using TVec4  = std::array< float, 4 >;
using TMat44 = std::array< TVec4, 4 >;

TVec3 Cross( TVec3 a, TVec3 b ) { return { a[1] * b[2] - a[2] * b[1], a[2] * b[0] - a[0] * b[2], a[0] * b[1] - a[1] * b[0] }; }
float Dot( TVec3 a, TVec3 b ) { return a[0]*b[0] + a[1]*b[1] + a[2]*b[2]; }
void Normalize( TVec3 & v )
{
    float len = sqrt( v[0] * v[0] + v[1] * v[1] + v[2] * v[2] );
    v[0] /= len; v[1] /= len; v[2] /= len;
}

TMat44 Camera::LookAt( const TVec3 &pos, const TVec3 &target, const TVec3 &up )
{ 
    TVec3 mz = { pos[0] - target[0], pos[1] - target[1], pos[2] - target[2] };
    Normalize( mz );
    TVec3 my = { up[0], up[1], up[2] };
    TVec3 mx = Cross( my, mz );
    Normalize( mx );
    my = Cross( mz, mx );

    TMat44 v{
        TVec4{ mx[0], my[0], mz[0], 0.0f },
        TVec4{ mx[1], my[1], mz[1], 0.0f },
        TVec4{ mx[2], my[2], mz[2], 0.0f },
        TVec4{ Dot(mx, pos), Dot(my, pos), -Dot(mz, pos), 1.0f }
    };

    return v;
}

Projection

The projection matrix describes the mapping from 3D points of a scene, to 2D points of the viewport. It transforms from eye space to the clip space, and the coordinates in the clip space are transformed to the normalized device coordinates (NDC) by dividing with the w component of the clip coordinates. The NDC are in range (-1,-1,-1) to (1,1,1).
Every geometry which is out of the NDC is clipped.

The objects between the near plane and the far plane of the camera frustum are mapped to the range (-1, 1) of the NDC.

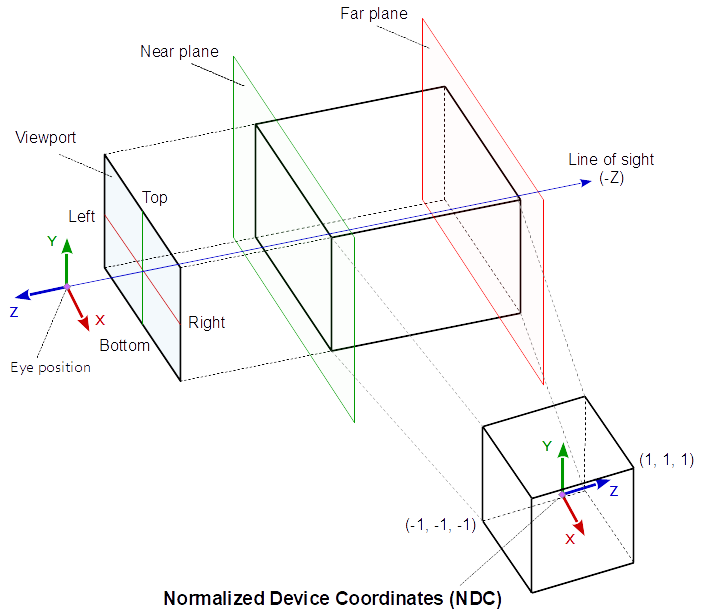
Orthographic Projection

At Orthographic Projection the coordinates in the eye space are linearly mapped to normalized device coordinates.

Orthographic Projection Matrix:

r = right, l = left, b = bottom, t = top, n = near, f = far 

2/(r-l)         0               0               0
0               2/(t-b)         0               0
0               0               -2/(f-n)        0
-(r+l)/(r-l)    -(t+b)/(t-b)    -(f+n)/(f-n)    1

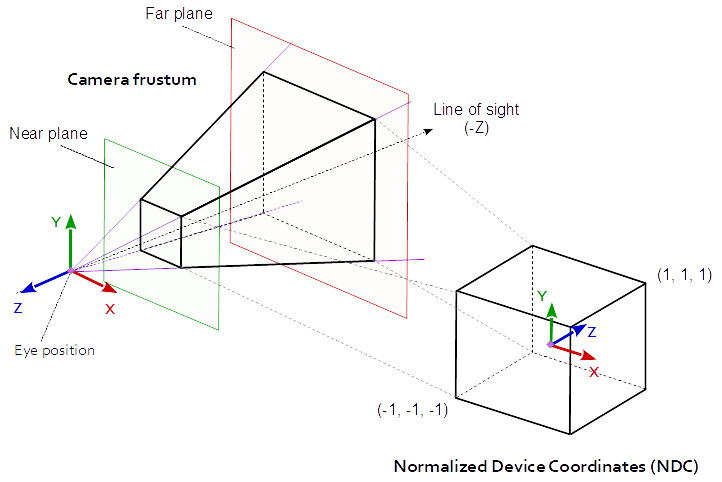
Perspective Projection

At Perspective Projection the projection matrix describes the mapping from 3D points in the world as they are seen from of a pinhole camera, to 2D points of the viewport.
The eye space coordinates in the camera frustum (a truncated pyramid) are mapped to a cube (the normalized device coordinates).

Perspective Projection Matrix:

r = right, l = left, b = bottom, t = top, n = near, f = far

2*n/(r-l)      0              0                0
0              2*n/(t-b)      0                0
(r+l)/(r-l)    (t+b)/(t-b)    -(f+n)/(f-n)    -1    
0              0              -2*f*n/(f-n)     0

where :

a = w / h
ta = tan( fov_y / 2 );

2 * n / (r-l) = 1 / (ta * a)
2 * n / (t-b) = 1 / ta

If the projection is symmetric, where the line of sight is in the center of the view port and the field of view is not displaced, then the matrix can be simplified:

1/(ta*a)  0     0              0
0         1/ta  0              0
0         0    -(f+n)/(f-n)   -1    
0         0    -2*f*n/(f-n)    0

The following function will calculate the same projection matrix as gluPerspective does:

#include <array>

const float cPI = 3.14159265f;
float ToRad( float deg ) { return deg * cPI / 180.0f; }

using TVec4  = std::array< float, 4 >;
using TMat44 = std::array< TVec4, 4 >;

TMat44 Perspective( float fov_y, float aspect )
{
    float fn = far + near
    float f_n = far - near;
    float r = aspect;
    float t = 1.0f / tan( ToRad( fov_y ) / 2.0f );

    return TMat44{ 
        TVec4{ t / r, 0.0f,  0.0f,                 0.0f },
        TVec4{ 0.0f,  t,     0.0f,                 0.0f },
        TVec4{ 0.0f,  0.0f, -fn / f_n,            -1.0f },
        TVec4{ 0.0f,  0.0f, -2.0f*far*near / f_n,  0.0f }
    };
}

3 Solutions to recover view space position in perspective projection

1. With field of view and aspect

Since the projection matrix is defined by the field of view and the aspect ratio it is possible to recover the viewport position with the field of view and the aspect ratio. Provided that it is a symmetrical perspective projection and the normalized device coordinates, the depth and the near and far plane are known.

Recover the Z distance in view space:

z_ndc = 2.0 * depth - 1.0;
z_eye = 2.0 * n * f / (f + n - z_ndc * (f - n));

Recover the view space position by the XY normalized device coordinates:

ndc_x, ndc_y = xy normalized device coordinates in range from (-1, -1) to (1, 1):

viewPos.x = z_eye * ndc_x * aspect * tanFov;
viewPos.y = z_eye * ndc_y * tanFov;
viewPos.z = -z_eye; 

2. With the projection matrix

The projection parameters, defined by the field of view and the aspect ratio are stored in the projection matrix. Therefore the viewport position can be recovered by the values from the projection matrix, from a symmetrical perspective projection.

Note the relation between projection matrix, field of view and aspect ratio:

prjMat[0][0] = 2*n/(r-l) = 1.0 / (tanFov * aspect);
prjMat[1][1] = 2*n/(t-b) = 1.0 / tanFov;

prjMat[2][2] = -(f+n)/(f-n)
prjMat[2][2] = -2*f*n/(f-n)

Recover the Z distance in view space:

A     = prj_mat[2][2];
B     = prj_mat[3][2];
z_ndc = 2.0 * depth - 1.0;
z_eye = B / (A + z_ndc);

Recover the view space position by the XY normalized device coordinates:

viewPos.x = z_eye * ndc_x / prjMat[0][0];
viewPos.y = z_eye * ndc_y / prjMat[1][1];
viewPos.z = -z_eye; 

3. With the inverse projection matrix

Of course the viewport position can be recovered by the inverse projection matrix.

mat4 inversePrjMat = inverse( prjMat );
vec4 viewPosH      = inversePrjMat * vec4(ndc_x, ndc_y, 2.0*depth - 1.0, 1.0)
vec3 viewPos       = viewPos.xyz / viewPos.w;

See further:

• How to render depth linearly in modern OpenGL with gl_FragCoord.z in fragment shader?
• Transform the modelMatrix
• Perspective projection and view matrix: Both depth buffer and triangle face orientation are reversed in OpenGL
• How to compute the size of the rectangle that is visible to the camera at a given coordinate?
• How to recover view space position given view space depth value and ndc xy
• Is it possble get which surface of cube will be click in OpenGL?

Brim

Thanks for the long answer, but I still can't understand how I will put the sphere in the coordinates I want from the mouse position – Bloodstream

Even though I haven't still implemented it, I mark your answer as accepted. I guess it was too much info to absorb but you have given me important knowledge. The "Mouse picking miss" video was really helpful and I was confused by two things. I didn't know how to get the necessary info to get the View and Projection matrix. Well, I was passing that info to gluLookAt and gluPerspective respectively. I feel kind of ashamed for not reading my old CS course code and forgetting what those two lines were doing. The OpenGL documentation about those functions explain it well too. – Bloodstream