Intersection area of a 3D Triangle and AABB

Question

I am looking to find the actual surface area of an intersection between a triangle and an AABB. Currently, I am using Tomas Akenine-Möller's AABB-Triangle intersection test, which works quite well - but I also need further information to improve the rendering quality of my realtime triangle-to-voxel engine I am developing.

The basic application of this will give me the ability to figure out which triangle from the original model takes up the most space in a given voxel. This allows me to associate the resulting voxels created from the model with the original triangle IDs, for not only color accuracy but persistance.

Sofar the approach I have thought of is take all intersection points of the triangle and the AABB, grouping them in pairs. Once you have all of the pairs, you can pretty easily find the third point associated with the pair that actually lies outside of the AABB. Then simply take the set of 3 vectors and construct triangles with them. Take the area of the full original triangle, and subtract the area of the constructed triangles. In the case that the triangle does not "primarily lie inside the AABB", you construct triangles that are inside the AABB and add them together, ignoring the overall area. I am not sure what to do yet if the triangle creates a non-triangular shape when intersecting the AABB. Here are some of the cases I came up with (there could be more) as 2D representations:

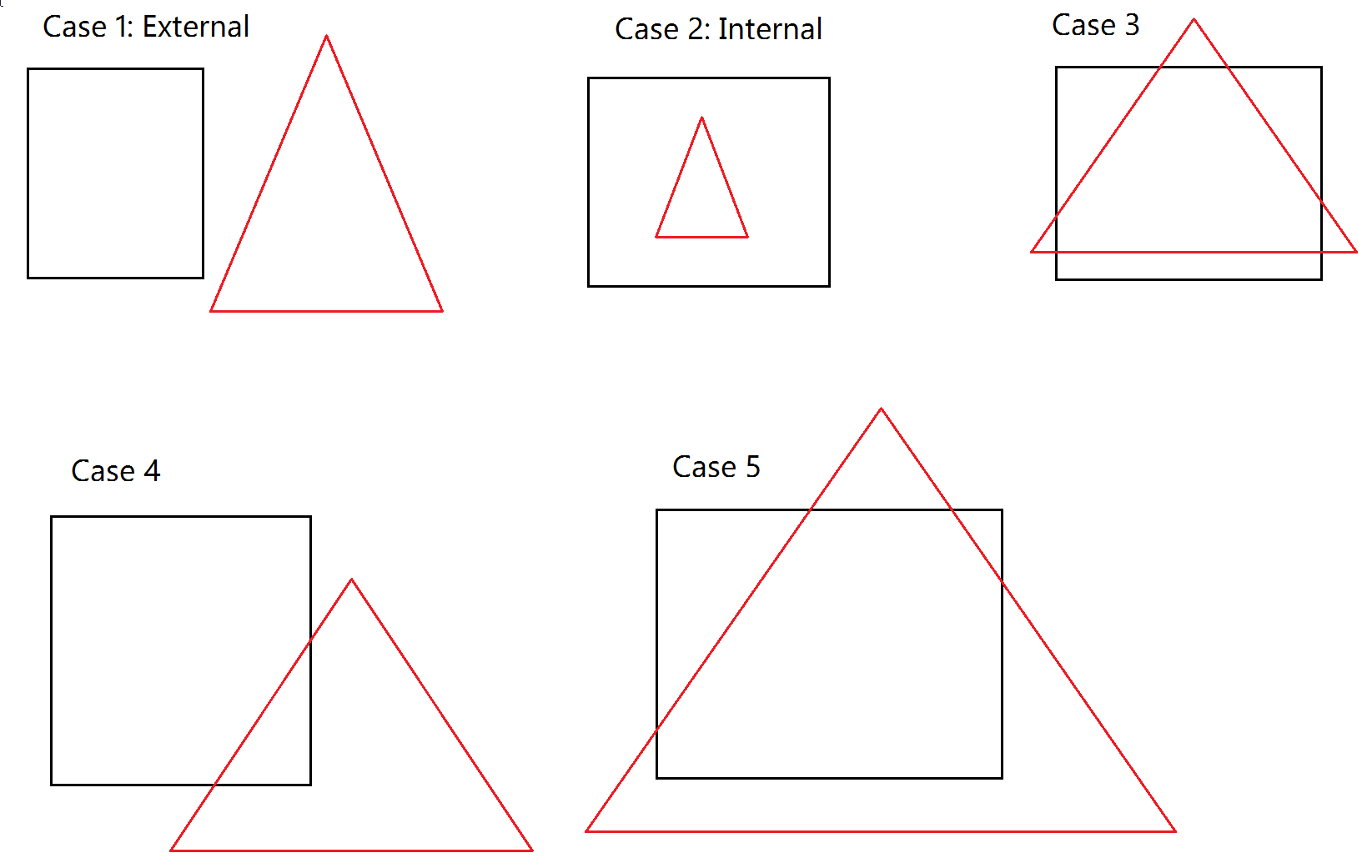
I really doubt the viability of my idea here, so I am open to any suggestions. If anyone might have a better solution given my particular problem that doesn't need the actual area, let me know.

Thanks.

Playoff

What is an "AABB"? – Kelci

where does Java get into it? What is the code you have so far to solve this issue? – Sevik

@RoryDaulton Axis-aligned bounding box (en.wikipedia.org/wiki/Bounding_volume). – Larine

Is the base/one side of your triangle axis-aligned? – Larine

Once you have determined the vertices of your shape, you can use the “Shoelace formula” to get the area. – Koenraad

@Sevik No code yet, but I'm not even sure how to solve Case 5 yet. – Playoff

@Sevik here is my Java implementation of the Tomas Akenine-Möller's AABB-Triangle intersection test: pastebin.com/tNRd7YTw – Playoff

So I know how to solve the fifth case, actually this solution would solve every possible case (but it's preferable not to use this solution because it's extremely slow): simply take the intersection points, decide which ones are interior, in the case that you have corners you simply add that point to the polygon you are constructing (instead of the intersection points), (...some steps...), and then you basically just produce a polygon of the internal area. Once you have the polygon, finding the area of it is easy. The problem with this solution, and my previously discussed solution: cost. – Playoff

Hi, have you figured out a proper way to process ? I would be very interested on how you did it ;) – Dejadeject

This ended up being a good resource for me fileadmin.cs.lth.se/cs/Personal/Tomas_Akenine-Moller/code/… @Dejadeject – Playoff