How to compute and plot a LOWESS curve in Python?

Question

How can I find and plot a LOWESS curve that looks like the following using Python?

I'm aware of the LOWESS implementation in statsmodels, but it doesn't seem to be able to give me 95% confidence interval lines that I can shade between. Seaborn has a method that calls the statsmodels implementation, but it can't plot the confidence intervals.

Other StackOverflow answers give code to draw a LOESS/LOWESS line, but none with a confidence interval. Can anyone assist with this? Is anyone aware of an existing implementation that would enable me to do this?

Thanks in advance.

Eburnation

Is this what you need? https://mcmap.net/q/399098/-how-can-i-plot-a-confidence-interval-in-python – Unblown

@ted930511 Thanks, but no; it looks like the previous comments were archived, but this question is about computing the appropriate confidence interval for a LOWESS curve. For searchers, the current answer is "use R if you want to compute LOWESS confidence intervals" or "implement them yourself from the original paper" if you must use Python. – Eburnation

As far as I know, you have to implement by yourself. Pls check this link – Unblown

Yup, looks like that blog post provides a usable implementation. I wish it had existed 3 years ago! If you leave an answer with that link and a short note on the contents of the blog, I'll mark it as the solution. – Eburnation

Answer 1

I found a link here is useful, and I put code below:

def lowess(x, y, f=1./3.):
    """
    Basic LOWESS smoother with uncertainty. 
    Note:
        - Not robust (so no iteration) and
             only normally distributed errors. 
        - No higher order polynomials d=1 
            so linear smoother.
    """
    # get some paras
    xwidth = f*(x.max()-x.min()) # effective width after reduction factor
    N = len(x) # number of obs
    # Don't assume the data is sorted
    order = np.argsort(x)
    # storage
    y_sm = np.zeros_like(y)
    y_stderr = np.zeros_like(y)
    # define the weigthing function -- clipping too!
    tricube = lambda d : np.clip((1- np.abs(d)**3)**3, 0, 1)
    # run the regression for each observation i
    for i in range(N):
        dist = np.abs((x[order][i]-x[order]))/xwidth
        w = tricube(dist)
        # form linear system with the weights
        A = np.stack([w, x[order]*w]).T
        b = w * y[order]
        ATA = A.T.dot(A)
        ATb = A.T.dot(b)
        # solve the syste
        sol = np.linalg.solve(ATA, ATb)
        # predict for the observation only
        yest = A[i].dot(sol)# equiv of A.dot(yest) just for k
        place = order[i]
        y_sm[place]=yest 
        sigma2 = (np.sum((A.dot(sol) -y [order])**2)/N )
        # Calculate the standard error
        y_stderr[place] = np.sqrt(sigma2 * 
                                A[i].dot(np.linalg.inv(ATA)
                                                    ).dot(A[i]))
    return y_sm, y_stderr


import numpy as np
import matplotlib.pyplot as plt


# make some data
x = 5*np.random.random(100)
y = np.sin(x) * 3*np.exp(-x) + np.random.normal(0, 0.2, 100)
order = np.argsort(x)

#run it
y_sm, y_std = lowess(x, y, f=1./5.)
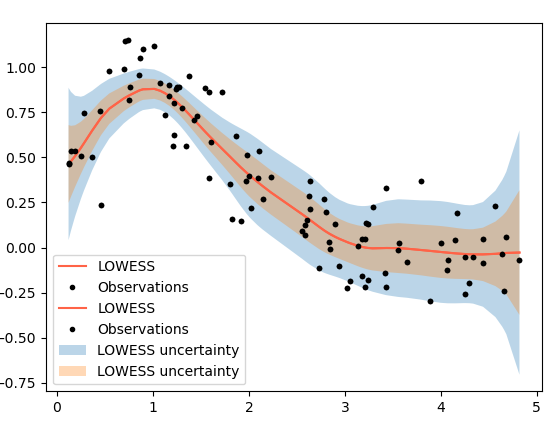
# plot it
plt.plot(x[order], y_sm[order], color='tomato', label='LOWESS')
plt.fill_between(x[order], y_sm[order] - 1.96*y_std[order],
                 y_sm[order] + 1.96*y_std[order], alpha=0.3, label='LOWESS uncertainty')
plt.plot(x, y, 'k.', label='Observations')
plt.legend(loc='best')
#run it
y_sm, y_std = lowess(x, y, f=1./5.)
# plot it
plt.plot(x[order], y_sm[order], color='tomato', label='LOWESS')
plt.fill_between(x[order], y_sm[order] - y_std[order],
                 y_sm[order] + y_std[order], alpha=0.3, label='LOWESS uncertainty')
plt.plot(x, y, 'k.', label='Observations')
plt.legend(loc='best')

Unblown