How can I plot a confidence interval in Python?

Question

I recently started to use Python, and I can't understand how to plot a confidence interval for a given datum (or set of data).

I already have a function that computes, given a set of measurements, a higher and lower bound depending on the confidence level that I pass to it, but how can I use those two values to plot a confidence interval?

Czerny

A good article about the topic of Confidence intervals in general, with some Python code: towardsdatascience.com/… – Kealey

Answer 1

There are several ways to accomplish what you asking for:

Using only matplotlib

from matplotlib import pyplot as plt
import numpy as np

#some example data
x = np.linspace(0.1, 9.9, 20)
y = 3.0 * x
#some confidence interval
ci = 1.96 * np.std(y)/np.sqrt(len(x))

fig, ax = plt.subplots()
ax.plot(x,y)
ax.fill_between(x, (y-ci), (y+ci), color='b', alpha=.1)

fill_between does what you are looking for. For more information on how to use this function, see: https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.fill_between.html

Output

Alternatively, go for seaborn, which supports this using lineplot or regplot, see: https://seaborn.pydata.org/generated/seaborn.lineplot.html

Plainspoken

Why do you divide by the mean? In ci = 1.96 * np.std(y)/np.mean(y). Shouldn't it by the square root of the sample size? According to Wikipedia: en.wikipedia.org/wiki/Confidence_interval#Basic_steps – Bruns

@CGFoX This is only a toy example. I agree, you would use the standard error. For illustration I used the mean which is not correct. The confidence interval for a linear regression is indeed even more intricate to calculate using the fitted parameters and a t-distribution for unknown SDs, which here is assumed to be normal hence 1.96 for 95 % confidence. – Plainspoken

Excellent solution! How can we add a label for the confidence interval to show in the legend? – Sinful

@Sinful You can supply a label string for the legend using label as argument when calling ax.fill_between . – Plainspoken

Answer 2

Let's assume that we have three categories and lower and upper bounds of confidence intervals of a certain estimator across these three categories:

data_dict = {}
data_dict['category'] = ['category 1','category 2','category 3']
data_dict['lower'] = [0.1,0.2,0.15]
data_dict['upper'] = [0.22,0.3,0.21]
dataset = pd.DataFrame(data_dict)

You can plot the confidence interval for each of these categories using the following code:

for lower,upper,y in zip(dataset['lower'],dataset['upper'],range(len(dataset))):
    plt.plot((lower,upper),(y,y),'ro-',color='orange')
plt.yticks(range(len(dataset)),list(dataset['category']))

Resulting with the following graph:

Snipe

Answer 3

import matplotlib.pyplot as plt
import statistics
from math import sqrt


def plot_confidence_interval(x, values, z=1.96, color='#2187bb', horizontal_line_width=0.25):
    mean = statistics.mean(values)
    stdev = statistics.stdev(values)
    confidence_interval = z * stdev / sqrt(len(values))

    left = x - horizontal_line_width / 2
    top = mean - confidence_interval
    right = x + horizontal_line_width / 2
    bottom = mean + confidence_interval
    plt.plot([x, x], [top, bottom], color=color)
    plt.plot([left, right], [top, top], color=color)
    plt.plot([left, right], [bottom, bottom], color=color)
    plt.plot(x, mean, 'o', color='#f44336')

    return mean, confidence_interval


plt.xticks([1, 2, 3, 4], ['FF', 'BF', 'FFD', 'BFD'])
plt.title('Confidence Interval')
plot_confidence_interval(1, [10, 11, 42, 45, 44])
plot_confidence_interval(2, [10, 21, 42, 45, 44])
plot_confidence_interval(3, [20, 2, 4, 45, 44])
plot_confidence_interval(4, [30, 31, 42, 45, 44])
plt.show()

• x: The x value of the input.
• values: An array containing the repeated values (usually measured values) of y corresponding to the value of x.
• z: The critical value of the z-distribution. Using 1.96 corresponds to the critical value of 95%.

Result:

Malathion

An explanation would be in order. E.g., what is the idea/gist? From the Help Center: "...always explain why the solution you're presenting is appropriate and how it works". Please respond by editing (changing) your answer, not here in comments (without "Edit:", "Update:", or similar - the answer should appear as if it was written today). – Dominion

Very good! You can also use hlines and vlines instead of plot – Rockoon

Answer 4

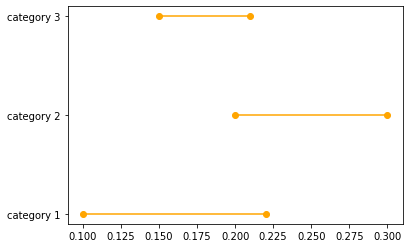
For a confidence interval across categories, building on what omer sagi suggested, let's say if we have a Pandas data frame with a column that contains categories (like category 1, category 2, and category 3) and another that has continuous data (like some kind of rating), here's a function using pd.groupby() and scipy.stats to plot difference in means across groups with confidence intervals:

import pandas as pd
import numpy as np
import scipy.stats as st

def plot_diff_in_means(data: pd.DataFrame, col1: str, col2: str):
    """
    Given data, plots difference in means with confidence intervals across groups
    col1: categorical data with groups
    col2: continuous data for the means
    """
    n = data.groupby(col1)[col2].count()
    # n contains a pd.Series with sample size for each category

    cat = list(data.groupby(col1, as_index=False)[col2].count()[col1])
    # 'cat' has the names of the categories, like 'category 1', 'category 2'

    mean = data.groupby(col1)[col2].agg('mean')
    # The average value of col2 across the categories

    std = data.groupby(col1)[col2].agg(np.std)
    se = std / np.sqrt(n)
    # Standard deviation and standard error

    lower = st.t.interval(alpha = 0.95, df=n-1, loc = mean, scale = se)[0]
    upper = st.t.interval(alpha = 0.95, df =n-1, loc = mean, scale = se)[1]
    # Calculates the upper and lower bounds using SciPy

    for upper, mean, lower, y in zip(upper, mean, lower, cat):
        plt.plot((lower, mean, upper), (y, y, y), 'b.-')
        # for 'b.-': 'b' means 'blue', '.' means dot, '-' means solid line
    plt.yticks(
        range(len(n)),
        list(data.groupby(col1, as_index = False)[col2].count()[col1])
        )

Given hypothetical data:

cat = ['a'] * 10 + ['b'] * 10 + ['c'] * 10
a = np.linspace(0.1, 5.0, 10)
b = np.linspace(0.5, 7.0, 10)
c = np.linspace(7.5, 20.0, 10)
rating = np.concatenate([a, b, c])

dat_dict = dict()
dat_dict['cat'] = cat
dat_dict['rating'] = rating
test_dat = pd.DataFrame(dat_dict)

which would look like this (but with more rows of course):

cat	rating
a	0.10000
a	0.64444
b	0.50000
b	0.12222
c	7.50000
c	8.88889

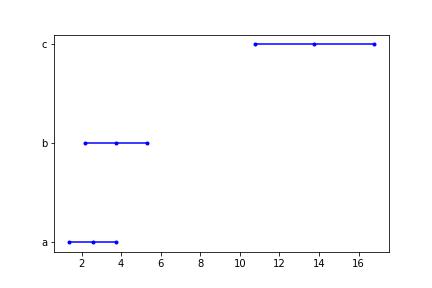
We can use the function to plot a difference in means with a confidence interval:

plot_diff_in_means(data = test_dat, col1 = 'cat', col2 = 'rating')

which gives us the following graph:

Copperas