Piecewise regression with a straight line and a horizontal line joining at a break point

Question

I want to do a piecewise linear regression with one break point, where the 2nd half of the regression line has slope = 0. There are examples of how to do a piecewise linear regression, such as here. The problem I'm having is I'm not clear how to fix the slope of half of the model to be 0.

I tried

lhs <- function(x) ifelse(x < k, k-x, 0)
rhs <- function(x) ifelse(x < k, 0, x-k)
fit <- lm(y ~ lhs(x) + rhs(x)) 

where k is the break point, but the segment on the right is not a flat / horizontal one.

I want to constrain the slope of the second segment at 0. I tried:

fit <- lm(y ~ x * (x < k) + x * (x > k))

but again, I'm not sure how to get the second half to have a zero slope.

Any help is greatly appreciated.

---

My own solution

I have a solution thanks to the comment below. Here's the code that I use to optimize and then plot the fit:

x <- c(1, 2, 3, 1, 2, 1, 6, 1, 2, 3, 2, 1, 4, 3, 1)
y <- c(0.041754212, 0.083491254, 0.193129615, 0.104249201, 0.17280516, 
0.154342335, 0.303370501, 0.025503008, 0.123934121, 0.191486527, 
0.183958737, 0.156707866, 0.31019215, 0.281890206, 0.25414608)

range_x <- max(x) - min(x)
intervals <- 1000
coef1 <- c()
coef2 <- c()
r2 <- c()

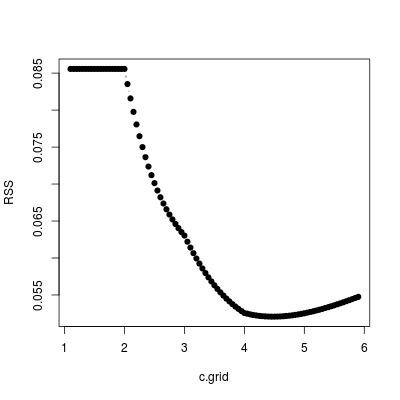
for (i in 1:intervals) {
  k <- min(x) + (i-1) * (range_x / intervals)     
  x2 = (x - k) * (x < k)
  fit <- lm(y ~ x2)
  coef1[i] <- summary(fit)$coef[1]
  coef2[i] <- summary(fit)$coef[2]
  r2[i] <- summary(fit)$r.squared
  }

best_r2 <- max(r2)   # get best r squared
pos <- which.max(r2)                                          
best_k <- min(x) + (pos - 1) * (range_x / intervals)

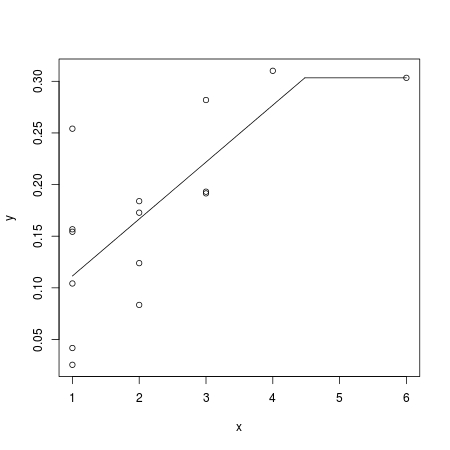
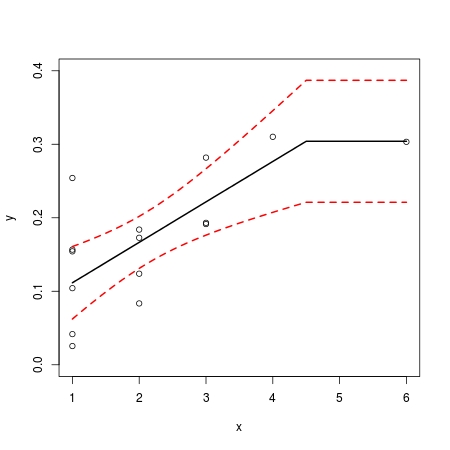
plot(x, y) 
curve(coef1[pos] - best_k * coef2[pos] + coef2[pos] * x,
      from=min(x), to=best_k, add = TRUE)
segments(best_k, coef1[pos], max(x), coef1[pos])

Accusatorial

What do your data look like? – Mopey

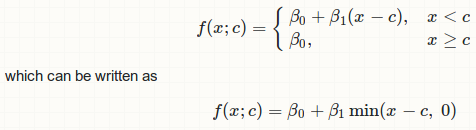
@Mopey x = c(1, 2, 3, 1, 2, 1, 6, 1, 2, 3, 2, 1, 4, 3, 1) y = c(0.041754212, 0.083491254, 0.193129615, 0.104249201, 0.17280516, 0.154342335, 0.303370501, 0.025503008, 0.123934121, 0.191486527, 0.183958737, 0.156707866, 0.31019215, 0.281890206, 0.025414608) I realize these data aren't great for the fit i'm describing but that's kind of the point... – Accusatorial

Answer 1

There is a very similar thread on Stack Overflow: Piecewise regression with a quadratic polynomial and a straight line joining smoothly at a break point. The only difference is that we now consider:

It turns out that functions est, choose.c and pred defined in my answer need not be changed at all; we only need to modify getX to return the design matrix for your piecewise regression:

getX <- function (x, c) cbind("beta0" = 1, "beta1" = pmin(x - c, 0))

Now, we follow the code in toy example to fit a model to your data:

x <- c(1, 2, 3, 1, 2, 1, 6, 1, 2, 3, 2, 1, 4, 3, 1)
y <- c(0.041754212, 0.083491254, 0.193129615, 0.104249201, 0.17280516, 
0.154342335, 0.303370501, 0.025503008, 0.123934121, 0.191486527, 
0.183958737, 0.156707866, 0.31019215, 0.281890206, 0.25414608)

x ranges from 1 to 6, so we consider

c.grid <- seq(1.1, 5.9, 0.05)
fit <- choose.c(x, y, c.grid)
fit$c
# 4.5

Finally we make prediction plot:

x.new <- seq(1, 6, by = 0.1)
p <- pred(fit, x.new)
plot(x, y, ylim = c(0, 0.4))
matlines(x.new, p[,-2], col = c(1,2,2), lty = c(1,2,2), lwd = 2)

We have rich information in the fitted model:

str(fit)
#List of 12
# $ coefficients : num [1:2] 0.304 0.055
# $ residuals    : num [1:15] -0.06981 -0.08307 -0.02844 -0.00731 0.00624 ...
# $ fitted.values: num [1:15] 0.112 0.167 0.222 0.112 0.167 ...
# $ R            : num [1:2, 1:2] -3.873 0.258 9.295 -4.37
# $ sig2         : num 0.00401
# $ coef.table   : num [1:2, 1:4] 0.3041 0.055 0.0384 0.0145 7.917 ...
#  ..- attr(*, "dimnames")=List of 2
#  .. ..$ : chr [1:2] "beta0" "beta1"
#  .. ..$ : chr [1:4] "Estimate" "Std. Error" "t value" "Pr(>|t|)"
# $ aic          : num -34.2
# $ bic          : num -39.5
# $ c            : num 4.5
# $ RSS          : num 0.0521
# $ r.squared    : num 0.526
# $ adj.r.squared: num 0.49

For example, we can inspect coefficients summary table:

fit$coef.table
#        Estimate Std. Error  t value     Pr(>|t|)
#beta0 0.30406634 0.03840657 7.917039 2.506043e-06
#beta1 0.05500095 0.01448188 3.797915 2.216095e-03

Exponible

Answer 2

Try making the variables outside the expression.

x2 = (x-k)*(x>k)
lm( y ~ x2)

Alternatively, you can use I()

lm(y~ I((x-k)*(x>k)))

I() takes whatever is inside literally and ignores other possible (mis)interpretations with whatever function it is inside of.

If you don't have a well-defined k, then you will have to optimize something like deviance over different values of k.

Viand

I'm confused about how this sets the slope of half of the line to 0? – Accusatorial

One half of the line will always be 0, because when(x<=k), (x>k) is FALSE, and FALSE * anynumber is 0. When x==k, it will be still zero because the function should be continuous. After that, (x-k) will increase at a constant rate. – Viand