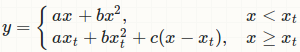This is an excellent exercise (maybe hard) to digest the theory and implementation of linear models. My answer will contain two parts:
- Part 1 (this one) introduces the parametrization I use and how this piecewise regression reduces to an ordinary least square problem. R functions including model estimation, break point selection and prediction are provided.
- Part 2 (the other one) demonstrates a toy, reproducible example on how to use those functions I have defined.
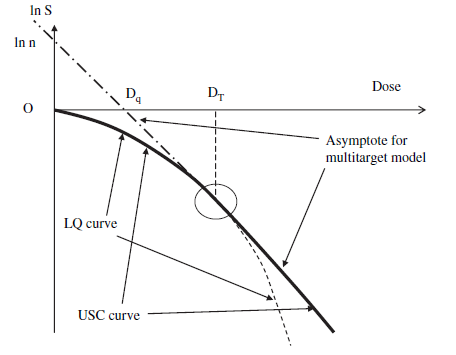
I have to use a different parametrization because the one you gave in your question is wrong! Your parametrization only ensures continuity of function value, but not the first derivative! That is why your fitted line is not tangent to the fitted quadratic polynomial at xt.
![Parametrization]()
## generate design matrix
getX <- function (x, c) {
x <- x - c
cbind("beta0" = 1, "beta1" = x, "beta2" = pmin(x, 0) ^ 2)
}
![Using AIC to select c]()
![Using RSS to select c]()
![grid search to find c]()
Function est below wraps up .lm.fit (for maximum efficiency) for estimation and inference of a model, at a given c:
## `x`, `y` give data points; `c` is known break point
est <- function (x, y, c) {
## model matrix
X <- getX(x, c)
p <- dim(X)[2L]
## solve least squares with QR factorization
fit <- .lm.fit(X, y)
## compute Pearson estimate of `sigma ^ 2`
r <- c(fit$residuals)
n <- length(r)
RSS <- c(crossprod(r))
sig2 <- RSS / (n - p)
## coefficients summary table
beta <- fit$coefficients
R <- "dimnames<-"(fit$qr[1:p, ], NULL)
Rinv <- backsolve(R, diag(p))
se <- sqrt(rowSums(Rinv ^ 2) * sig2)
tstat <- beta / se
pval <- 2 * pt(abs(tstat), n - p, lower.tail = FALSE)
tab <- matrix(c(beta, se, tstat, pval), nrow = p, ncol = 4L,
dimnames = list(dimnames(X)[[2L]],
c("Estimate", "Std. Error", "t value", "Pr(>|t|)")))
## 2 * negative log-likelihood
nega2logLik <- n * log(2 * pi * sig2) + (n - p)
## AIC / BIC
aic <- nega2logLik + 2 * (p + 1)
bic <- nega2logLik + log(n) * (p + 1)
## multiple R-squared and adjusted R-squared
TSS <- c(crossprod(y - sum(y) / n))
r.squared <- 1 - RSS / TSS
adj.r.squared <- 1 - sig2 * (n - 1) / TSS
## return
list(coefficients = beta, residuals = r, fitted.values = c(X %*% beta),
R = R, sig2 = sig2, coef.table = tab, aic = aic, bic = bic, c = c,
RSS = RSS, r.squared = r.squared, adj.r.squared = adj.r.squared)
}
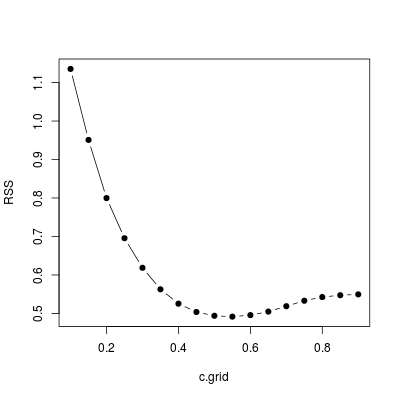
As you can see, it also returns various summary as if summary.lm has been called. Now let's write another wrapper function choose.c. It sketch RSS against c.grid and return the best model with selected c.
choose.c <- function (x, y, c.grid) {
if (is.unsorted(c.grid)) stop("'c.grid' in not increasing")
## model list
lst <- lapply(c.grid, est, x = x, y = y)
## RSS trace
RSS <- sapply(lst, "[[", "RSS")
## verbose
plot(c.grid, RSS, type = "b", pch = 19)
## find `c` / the model minimizing `RSS`
lst[[which.min(RSS)]]
}
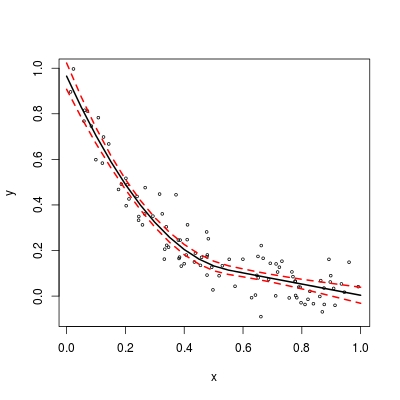
So far so good. To complete the story, we also want a predict routine.
pred <- function (model, x.new) {
## prediction matrix
X <- getX(x.new, model$c)
p <- dim(X)[2L]
## predicted mean
fit <- X %*% model$coefficients
## prediction standard error
Qt <- forwardsolve(t(model$R), t(X))
se <- sqrt(colSums(Qt ^ 2) * model$sig2)
## 95%-confidence interval
alpha <- qt(0.025, length(model$residuals) - p)
lwr <- fit + alpha * se
upr <- fit - alpha * se
## return
matrix(c(fit, se, lwr, upr), ncol = 4L,
dimnames = list(NULL, c("fit", "se", "lwr", "upr")))
}