How to generate random normal distribution without numpy? (Google interview)

Question

So I have a data science interview at Google, and I'm trying to prepare. One of the questions I see a lot (on Glassdoor) from people who have interviewed there before has been: "Write code to generate random normal distribution." While this is easy to do using numpy, I know sometimes Google asks the candidate to code without using any packages or libraries, so basically from scratch.

Any ideas?

Polyhydroxy

Does this answer your question? Converting a Uniform Distribution to a Normal Distribution – Interoceptor

You must check the normal distribution theory. Because you need calculated some variables, with the froms of theory. – Agamogenesis

random.gauss() ? – Irmgardirmina

Answer 1

According to the Central Limit Theorem a normalised summation of independent random variables will approach a normal distribution. The simplest demonstration of this is adding two dice together.

So maybe something like:

import random
import matplotlib.pyplot as plt

def pseudo_norm():
    """Generate a value between 1-100 in a normal distribution"""
    count = 10
    values =  sum([random.randint(1, 100) for x in range(count)])
    return round(values/count)
    
dist = [pseudo_norm() for x in range(10_000)]
n_bins = 100
fig, ax = plt.subplots()
ax.set_title('Pseudo-normal')
hist = ax.hist(dist, bins=n_bins)
plt.show()

Which generates something like:

Vivian

Answer 2

(Probably a bit late to the party but I had the same question and found a different solution which I personally prefer.)

You can use the Box-Muller Transform to generate two independent random real numbers z_0 and z_1 that follow a standard normal distribution (zero mean and unit variance) using two uniformly distributed numbers u_1 and u_2 .

Example

If you want to generate N random numbers that follow a normal distribution just like np.random.randn(n) does you can do something like the following:

import math
import random

rands = []
for i in range(N):
    u1 = random.uniform(0, 1)
    u2 = random.uniform(0, 1)
    
    z0 = math.sqrt(-2 * math.log(u1)) * math.cos(2 * math.pi * u2)
    rands.append(z0)
    # z1 can be discarded (or cached for a more efficient approach)
    # z1 = math.sqrt(-2 * math.log(u1)) * math.sin(2 * math.pi * u2)

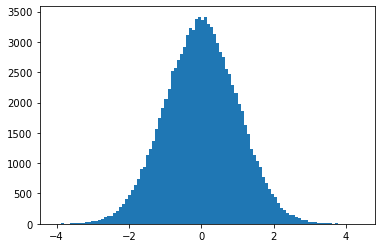
If you plot a histogram of rands you'll verify the numbers are indeed normally distributed. The following is the distribution of 100000 random numbers with 100 bins:

Levantine