How do you calculate the average of a set of circular data?

Question

I want to calculate the average of a set of circular data. For example, I might have several samples from the reading of a compass. The problem of course is how to deal with the wraparound. The same algorithm might be useful for a clockface.

The actual question is more complicated - what do statistics mean on a sphere or in an algebraic space which "wraps around", e.g. the additive group mod n. The answer may not be unique, e.g. the average of 359 degrees and 1 degree could be 0 degrees or 180, but statistically 0 looks better.

This is a real programming problem for me and I'm trying to make it not look like just a Math problem.

Theologue

By average angle, I assume your actually want mean bearing. An angle exists between two lines, a bearing is the direction of a single line. In this case, starblue has it right. – Forbis

@Nick Fortescue: can you update your question to be more specific: do you mean angles or a bearing? – Australian

I actually wanted something slightly more complicated (but is analogous to bearings) and was trying to simplify to make the question easier, and as usual made it more complicated. I found the answer I wanted at catless.ncl.ac.uk/Risks/7.44.html#subj4. I'll re-edit the qn. – Theologue

The Risks answer is basically what I'm proposing, except that it may run into trouble when the denominator is 0. – Roye

Interesting article on the meaning of angles: twistedoakstudios.com/blog/?p=938 – Roye

This is also the technique needed for calculating the average hue of pixels. (It is not the same thing to average pixels in RGB then convert to HSB/HSL afterwards!) – Depredation

@ShaneMacLaughlin that is not a meaningful distinction. the direction of a single line is always going to be relative to some axis (i.e., another line). – Collected

@dbliss, hugely important distinction. By definition, bearings share a common axis which is typically grid North, directions do not. A theodolite for example measures horizontal directions relative to an arbitrary axis, which changes to a new arbitrary axis each time you move the theodolite. Over three decades working in the land survey domain and I still regularly have to explain the difference to people between angles, whole circle bearings, quadrant bearings, and horizontal directions. – Forbis

@ShaneMacLaughlin you're very deep into jargon and distinctions that are "hugely important" only within your seemingly very narrow domain. the general term for the sort of data the questioner is asking about is "circular data," not bearings. circular data encompasses times on a clock, directions (as normally understood, not whatever you're talking about), colors, orientations, etc. – Collected

@dbliss, you just edited the question and replaced the term angles with circular data to make it better fit your own comment! Really???? To clarify, the original question was already edited by the OP to read 'to resolve all the confusion, when I refer to angles you can assume I mean bearings' If you honestly believe measurement of angles and bearings is a very narrow domain, can I assume you never studied trigonometry at school, don't have GPS on your phone, nor have ever used google earth.. – Forbis

To further clarify difference between bearings and angles in the context given of a clock face, If I look at the clock at midday, both hands have a bearing of 0 degrees. If I look at the clock 1 day later, they still have a bearing of 0 degrees, but the big hand has travelled 720 degrees in a clockwise direction. So mean bearing would equate to mean time of day, whereas mean angle would equate to mean amount of time spent. IMHO, crucial distinction in the context of the original question. – Forbis

Answer 1

Compute unit vectors from the angles and take the angle of their average.

Roye

That does not work if the vectors cancel each other out. Average could still be meaningful in this case, depending on its exact definition. – Glutenous

@David, the average direction of two bearings 180 degrees out is undefined. This doesn't make starblue's answer wrong, it's just an exceptional case, as occurs in many geomteric problems. – Forbis

I don't think there is a meaningful definition which takes into account circularity when the vectors cancel out. – Roye

@smacl: I agree, if angles represent directions. But if you think of complex numbers, for example, and define average as "what is the argument of c, such that cc == ab", where a and b have a modulus of 1, then the average of 0 and 180 is 90. – Glutenous

By the way this is also a great answer because it gives an obvious extension to weighted average if you trust some samples more than others. – Theologue

The average of 0,0,90 won't come 30! – Cockatoo

@starblue: atan( (sin(0)+sin(0)+sin(90)) / (cos(0)+cos(0)+cos(90)) ) = atan(1/2)= 26.56 deg – Cockatoo

It is disappointing to have the accepted answer falling into this usual trap. This method gives a reasonable answer only if the angles are fairly focused. However, if you have a wide spread of angles, this is useless. – Enrichetta

See also math.stackexchange.com/questions/14530/… – Roye

@PierreBdR: If I take two steps in direction 0deg and one in direction 90deg I will have moved in the direction 26.56 deg relative to where I started. In this sense 26.56 makes much more sense as the average direction of {0,0,90} deg than 30 deg. The algebraic average is just one of many possible averages (see en.wikipedia.org/wiki/Mean )-- and it seems quite irrelevant for the purpose of averaging directions (just as it does for many others). – Insistent

@DavidHanak: Why not -90? Either answer is correct, because 180 degrees is the same as -180 degrees. There is no real single-valued answer. – Melanymelaphyre

@Enrichetta The length of the mean vector denotes the concentration (mean-trustworthiness) of a given circular dataset. What is useless is trying to calculate the mean of a poorly-clustered dataset, not the formula. – Orbit

A python implementation is available in scipy: docs.scipy.org/doc/scipy/reference/generated/… – Damnify

Answer 2

This question is examined in detail in the book: "Statistics On Spheres", Geoffrey S. Watson, University of Arkansas Lecture Notes in the Mathematical Sciences, 1983 John Wiley & Sons, Inc. as mentioned at http://catless.ncl.ac.uk/Risks/7.44.html#subj4 by Bruce Karsh.

A good way to estimate an average angle, A, from a set of angle measurements a[i] 0<=i

                   sum_i_from_1_to_N sin(a[i])
a = arctangent ---------------------------
                   sum_i_from_1_to_N cos(a[i])

The method given by starblue is computationally equivalent, but his reasons are clearer and probably programmatically more efficient, and also work well in the zero case, so kudos to him.

The subject is now explored in more detail on Wikipedia, and with other uses, like fractional parts.

Theologue

which is also much the same as the algorithm I posted at the same time as you. You would need to use atan2 rather than a plain atan, though, since otherwise you can't tell which quadrant the answer is in. – Dzerzhinsk

You can still end up with some indeterminate answers. Like in the 0, 180 sample. So you still have to check for edge cases. Also, there is usually an atan2 function available which might be faster in your case. – Armrest

Answer 3

I see the problem - for example, if you have a 45' angle and a 315' angle, the "natural" average would be 180', but the value you want is actually 0'.

I think Starblue is onto something. Just calculate the (x, y) cartesian coordinates for each angle, and add those resulting vectors together. The angular offset of the final vector should be your required result.

x = y = 0
foreach angle {
    x += cos(angle)
    y += sin(angle)
}
average_angle = atan2(y, x)

I'm ignoring for now that a compass heading starts at north, and goes clockwise, whereas "normal" cartesian coordinates start with zero along the X axis, and then go anti-clockwise. The maths should work out the same way regardless.

Dzerzhinsk

Your maths library probably uses Radians for angles. Remember to convert. – Dicarlo

Maybe it's too late at night, but using this logic, I get an average angle of 341.8947... instead of 342 for angles of [ 320, 330, 340, 350, 10, ]. Anyone see my typo? – Clariceclarie

@AlexRobinson it's not a typo, it's because the final angle is simply the eventual angle obtained by taking a set of steps of each of those angles individually. – Dzerzhinsk

@AlexRobinson, to be more specific: cos(), sin() and atan2() give approximations (good ones, but still off by 1 or 2 ulps) so the more you average, the more errors you include. – Sangraal

Answer 4

FOR THE SPECIAL CASE OF TWO ANGLES:

The answer ( (a + b) mod 360 ) / 2 is WRONG. For angles 350 and 2, the closest point is 356, not 176.

The unit vector and trig solutions may be too expensive.

What I've got from a little tinkering is:

diff = ( ( a - b + 180 + 360 ) mod 360 ) - 180
angle = (360 + b + ( diff / 2 ) ) mod 360

• 0, 180 -> 90 (two answers for this: this equation takes the clockwise answer from a)
• 180, 0 -> 270 (see above)
• 180, 1 -> 90.5
• 1, 180 -> 90.5
• 20, 350 -> 5
• 350, 20 -> 5 (all following examples reverse properly too)
• 10, 20 -> 15
• 350, 2 -> 356
• 359, 0 -> 359.5
• 180, 180 -> 180

Psychosexual

This could further be optimized by the use of BAMS: #1049445 – Psychosexual

Not bad. The first line computes the relative angle of a with respect to b in the range [-180, 179], the second computes the middle angle from that. I'd use b + diff/2 instead of a - diff/2 for clarity. – Roye

Am I missing something? I DO get 295. – Psychosexual

Ah.. I get it. Matlab's mod operator wraps -10 to 350. I'll change the code. It's a simple additional 360. – Psychosexual

Another nice feature of this method is that it's easy to implement a weighted average of the two angles. In the second line, multiply diff by the weight of the first angle and replace the 2 in the denominator with the sum of the weights. angle = (360 + b + (WEIGHT[a] * diff / (WEIGHT[a] + WEIGHT[b]))) mod 360 – Trousseau

Answer 5

ackb is right that these vector based solutions cannot be considered true averages of angles, they are only an average of the unit vector counterparts. However, ackb's suggested solution does not appear to mathematically sound.

The following is a solution that is mathematically derived from the goal of minimising (angle[i] - avgAngle)^2 (where the difference is corrected if necessary), which makes it a true arithmetic mean of the angles.

First, we need to look at exactly which cases the difference between angles is different to the difference between their normal number counterparts. Consider angles x and y, if y >= x - 180 and y <= x + 180, then we can use the difference (x-y) directly. Otherwise, if the first condition is not met then we must use (y+360) in the calculation instead of y. Corresponding, if the second condition is not met then we must use (y-360) instead of y. Since the equation of the curve we are minimising only changes at the points where these inequalities change from true to false or vice versa, we can separate the full [0,360) range into a set of segments, separated by these points. Then, we only need to find the minimum of each of these segments, and then the minimum of each segment's minimum, which is the average.

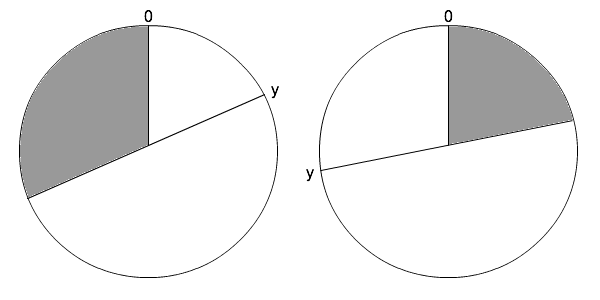
Here's an image demonstrating where the problems occur in calculating angle differences. If x lies in the gray area then there will be a problem.

To minimise a variable, depending on the curve, we can take the derivative of what we want to minimise and then we find the turning point (which is where the derivative = 0).

Here we will apply the idea of minimise the squared difference to derive the common arithmetic mean formula: sum(a[i])/n. The curve y = sum((a[i]-x)^2) can be minimised in this way:

y = sum((a[i]-x)^2)
= sum(a[i]^2 - 2*a[i]*x + x^2)
= sum(a[i]^2) - 2*x*sum(a[i]) + n*x^2

dy\dx = -2*sum(a[i]) + 2*n*x

for dy/dx = 0:
-2*sum(a[i]) + 2*n*x = 0
-> n*x = sum(a[i])
-> x = sum(a[i])/n

Now applying it to curves with our adjusted differences:

b = subset of a where the correct (angular) difference a[i]-x c = subset of a where the correct (angular) difference (a[i]-360)-x cn = size of c d = subset of a where the correct (angular) difference (a[i]+360)-x dn = size of d

y = sum((b[i]-x)^2) + sum(((c[i]-360)-b)^2) + sum(((d[i]+360)-c)^2)
= sum(b[i]^2 - 2*b[i]*x + x^2)
  + sum((c[i]-360)^2 - 2*(c[i]-360)*x + x^2)
  + sum((d[i]+360)^2 - 2*(d[i]+360)*x + x^2)
= sum(b[i]^2) - 2*x*sum(b[i])
  + sum((c[i]-360)^2) - 2*x*(sum(c[i]) - 360*cn)
  + sum((d[i]+360)^2) - 2*x*(sum(d[i]) + 360*dn)
  + n*x^2
= sum(b[i]^2) + sum((c[i]-360)^2) + sum((d[i]+360)^2)
  - 2*x*(sum(b[i]) + sum(c[i]) + sum(d[i]))
  - 2*x*(360*dn - 360*cn)
  + n*x^2
= sum(b[i]^2) + sum((c[i]-360)^2) + sum((d[i]+360)^2)
  - 2*x*sum(x[i])
  - 2*x*360*(dn - cn)
  + n*x^2

dy/dx = 2*n*x - 2*sum(x[i]) - 2*360*(dn - cn)

for dy/dx = 0:
2*n*x - 2*sum(x[i]) - 2*360*(dn - cn) = 0
n*x = sum(x[i]) + 360*(dn - cn)
x = (sum(x[i]) + 360*(dn - cn))/n

This alone is not quite enough to get the minimum, while it works for normal values, that has an unbounded set, so the result will definitely lie within set's range and is therefore valid. We need the minimum within a range (defined by the segment). If the minimum is less than our segment's lower bound then the minimum of that segment must be at the lower bound (because quadratic curves only have 1 turning point) and if the minimum is greater than our segment's upper bound then the segment's minimum is at the upper bound. After we have the minimum for each segment, we simply find the one that has the lowest value for what we're minimising (sum((b[i]-x)^2) + sum(((c[i]-360)-b)^2) + sum(((d[i]+360)-c)^2)).

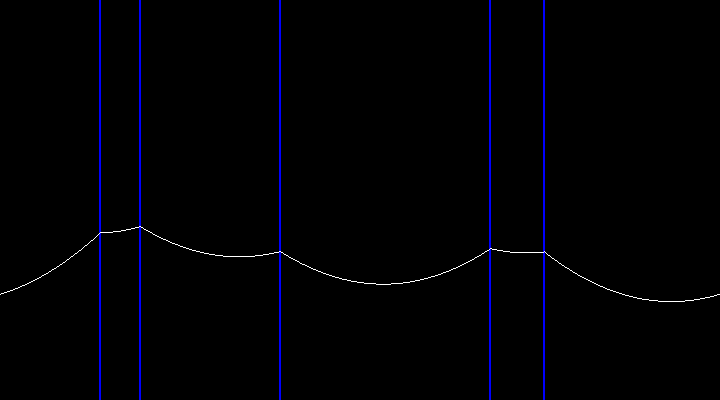
Here is an image to the curve, which shows how it changes at the points where x=(a[i]+180)%360. The data set is in question is {65,92,230,320,250}.

Here is an implementation of the algorithm in Java, including some optimisations, its complexity is O(nlogn). It can be reduced to O(n) if you replace the comparison based sort with a non comparison based sort, such as radix sort.

static double varnc(double _mean, int _n, double _sumX, double _sumSqrX)
{
    return _mean*(_n*_mean - 2*_sumX) + _sumSqrX;
}
//with lower correction
static double varlc(double _mean, int _n, double _sumX, double _sumSqrX, int _nc, double _sumC)
{
    return _mean*(_n*_mean - 2*_sumX) + _sumSqrX
            + 2*360*_sumC + _nc*(-2*360*_mean + 360*360);
}
//with upper correction
static double varuc(double _mean, int _n, double _sumX, double _sumSqrX, int _nc, double _sumC)
{
    return _mean*(_n*_mean - 2*_sumX) + _sumSqrX
            - 2*360*_sumC + _nc*(2*360*_mean + 360*360);
}

static double[] averageAngles(double[] _angles)
{
    double sumAngles;
    double sumSqrAngles;

    double[] lowerAngles;
    double[] upperAngles;

    {
        List<Double> lowerAngles_ = new LinkedList<Double>();
        List<Double> upperAngles_ = new LinkedList<Double>();

        sumAngles = 0;
        sumSqrAngles = 0;
        for(double angle : _angles)
        {
            sumAngles += angle;
            sumSqrAngles += angle*angle;
            if(angle < 180)
                lowerAngles_.add(angle);
            else if(angle > 180)
                upperAngles_.add(angle);
        }


        Collections.sort(lowerAngles_);
        Collections.sort(upperAngles_,Collections.reverseOrder());


        lowerAngles = new double[lowerAngles_.size()];
        Iterator<Double> lowerAnglesIter = lowerAngles_.iterator();
        for(int i = 0; i < lowerAngles_.size(); i++)
            lowerAngles[i] = lowerAnglesIter.next();

        upperAngles = new double[upperAngles_.size()];
        Iterator<Double> upperAnglesIter = upperAngles_.iterator();
        for(int i = 0; i < upperAngles_.size(); i++)
            upperAngles[i] = upperAnglesIter.next();
    }

    List<Double> averageAngles = new LinkedList<Double>();
    averageAngles.add(180d);
    double variance = varnc(180,_angles.length,sumAngles,sumSqrAngles);

    double lowerBound = 180;
    double sumLC = 0;
    for(int i = 0; i < lowerAngles.length; i++)
    {
        //get average for a segment based on minimum
        double testAverageAngle = (sumAngles + 360*i)/_angles.length;
        //minimum is outside segment range (therefore not directly relevant)
        //since it is greater than lowerAngles[i], the minimum for the segment
        //must lie on the boundary lowerAngles[i]
        if(testAverageAngle > lowerAngles[i]+180)
            testAverageAngle = lowerAngles[i];

        if(testAverageAngle > lowerBound)
        {
            double testVariance = varlc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,i,sumLC);

            if(testVariance < variance)
            {
                averageAngles.clear();
                averageAngles.add(testAverageAngle);
                variance = testVariance;
            }
            else if(testVariance == variance)
                averageAngles.add(testAverageAngle);
        }

        lowerBound = lowerAngles[i];
        sumLC += lowerAngles[i];
    }
    //Test last segment
    {
        //get average for a segment based on minimum
        double testAverageAngle = (sumAngles + 360*lowerAngles.length)/_angles.length;
        //minimum is inside segment range
        //we will test average 0 (360) later
        if(testAverageAngle < 360 && testAverageAngle > lowerBound)
        {
            double testVariance = varlc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,lowerAngles.length,sumLC);

            if(testVariance < variance)
            {
                averageAngles.clear();
                averageAngles.add(testAverageAngle);
                variance = testVariance;
            }
            else if(testVariance == variance)
                averageAngles.add(testAverageAngle);
        }
    }


    double upperBound = 180;
    double sumUC = 0;
    for(int i = 0; i < upperAngles.length; i++)
    {
        //get average for a segment based on minimum
        double testAverageAngle = (sumAngles - 360*i)/_angles.length;
        //minimum is outside segment range (therefore not directly relevant)
        //since it is greater than lowerAngles[i], the minimum for the segment
        //must lie on the boundary lowerAngles[i]
        if(testAverageAngle < upperAngles[i]-180)
            testAverageAngle = upperAngles[i];

        if(testAverageAngle < upperBound)
        {
            double testVariance = varuc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,i,sumUC);

            if(testVariance < variance)
            {
                averageAngles.clear();
                averageAngles.add(testAverageAngle);
                variance = testVariance;
            }
            else if(testVariance == variance)
                averageAngles.add(testAverageAngle);
        }

        upperBound = upperAngles[i];
        sumUC += upperBound;
    }
    //Test last segment
    {
        //get average for a segment based on minimum
        double testAverageAngle = (sumAngles - 360*upperAngles.length)/_angles.length;
        //minimum is inside segment range
        //we test average 0 (360) now           
        if(testAverageAngle < 0)
            testAverageAngle = 0;

        if(testAverageAngle < upperBound)
        {
            double testVariance = varuc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,upperAngles.length,sumUC);

            if(testVariance < variance)
            {
                averageAngles.clear();
                averageAngles.add(testAverageAngle);
                variance = testVariance;
            }
            else if(testVariance == variance)
                averageAngles.add(testAverageAngle);
        }
    }


    double[] averageAngles_ = new double[averageAngles.size()];
    Iterator<Double> averageAnglesIter = averageAngles.iterator();
    for(int i = 0; i < averageAngles_.length; i++)
        averageAngles_[i] = averageAnglesIter.next();


    return averageAngles_;
}

The arithmetic mean of a set of angles may not agree with your intuitive idea of what the average should be. For example, the arithmetic mean of the set {179,179,0,181,181} is 216 (and 144). The answer you immediately think of is probably 180, however it is well known that the arithmetic mean is heavily affected by edge values. You should also remember that angles are not vectors, as appealing as that may seem when dealing with angles sometimes.

This algorithm does of course also apply to all quantities that obey modular arithmetic (with minimal adjustment), such as the time of day.

I would also like to stress that even though this is a true average of angles, unlike the vector solutions, that does not necessarily mean it is the solution you should be using, the average of the corresponding unit vectors may well be the value you actually should to be using.

Friary

The Mitsuta method actually gives the starting angle + the average of the rotations from the starting angle. So to get a similar method, accounting for measurement error then you'd need to be looking at the rotations happening and estimate the error for those. I think you would need a distribution for the rotations in order to estimate an error for them. – Friary

Answer 6

I'd like to share an method I used with a microcontroller which did not have floating point or trigonometry capabilities. I still needed to "average" 10 raw bearing readings in order to smooth out variations.

1. Check whether the first bearing is the range 270-360 or 0-90 degrees (northern two quadrants)
2. If it is, rotate this and all subsequent readings by 180 degrees, keeping all values in the range 0 <= bearing < 360. Otherwise take the readings as they come.
3. Once 10 readings have been taken calculate the numerical average assuming that there has been no wraparound
4. If the 180 degree rotation had been in effect then rotate the calculated average by 180 degrees to get back to a "true" bearing.

It's not ideal; it can break. I got away with it in this case because the device only rotates very slowly. I'll put it out there in case anyone else finds themselves working under similar restrictions.

Kura

Answer 7

You have to define average more accurately. For the specific case of two angles, I can think of two different scenarios:

1. The "true" average, i.e. (a + b) / 2 % 360.
2. The angle that points "between" the two others while staying in the same semicircle, e.g. for 355 and 5, this would be 0, not 180. To do this, you need to check if the difference between the two angles is larger than 180 or not. If so, increment the smaller angle by 360 before using the above formula.

I don't see how the second alternative can be generalized for the case of more than two angles, though.

Glutenous

While the question refers to angles, it is better thought of as mean direction, and is a common navigation issue. – Forbis

Good points, David. For instance, what is the average of a 180º angle and a 540º angle? Is it 360º or 180º? – Polydactyl

@Baltimark, I guess it depends on what you are doing. If its navigation, probably the latter. If it's a fancy snowboarding jump, maybe the former ;) – Forbis

So the "true" average of 1 and 359 is (360 / 2) % 360 = 180?? I think not. – Evania

@Die in Sente: numerically speaking, definitely. For example, if angles represent turns, not directions, then the average of 359 and 1 is surely 180. It's all a matter of interpretation. – Glutenous

"True?" No, "arithmetic" is what you wanted to say. – Orbit

Answer 8

In python, with angles between [-180, 180)

def add_angles(a, b):
  return (a + b + 180) % 360 - 180

def average_angles(a, b):
  return add_angles(a, add_angles(-a, b)/2)

Details:

For the average of two angles there are two averages 180° apart, but we may want the closer average.

Visually, the average of the blue (b) and green (a) the yields the teal point:

Angles 'wrap around' (e.g. 355 + 10 = 5), but standard arithmetic will ignore this branch point. However if angle b is opposite to the branch point, then (b + g)/2 gives the closest average: the teal point.

For any two angles, we can rotate the problem so one of the angles is opposite to the branch point, perform standard averaging, then rotate back.

Tenement

Answer 9

Like all averages, the answer depends upon the choice of metric. For a given metric M, the average of some angles a_k in [-pi,pi] for k in [1,N] is that angle a_M which minimizes the sum of squared distances d^2_M(a_M,a_k). For a weighted mean, one simply includes in the sum the weights w_k (such that sum_k w_k = 1). That is,

a_M = arg min_x sum_k w_k d^2_M(x,a_k)

Two common choices of metric are the Frobenius and the Riemann metrics. For the Frobenius metric, a direct formula exists that corresponds to the usual notion of average bearing in circular statistics. See "Means and Averaging in the Group of Rotations", Maher Moakher, SIAM Journal on Matrix Analysis and Applications, Volume 24, Issue 1, 2002, for details.
http://link.aip.org/link/?SJMAEL/24/1/1

Here's a function for GNU Octave 3.2.4 that does the computation:

function ma=meanangleoct(a,w,hp,ntype)
%   ma=meanangleoct(a,w,hp,ntype) returns the average of angles a
%   given weights w and half-period hp using norm type ntype
%   Ref: "Means and Averaging in the Group of Rotations",
%   Maher Moakher, SIAM Journal on Matrix Analysis and Applications,
%   Volume 24, Issue 1, 2002.

if (nargin<1) | (nargin>4), help meanangleoct, return, end 
if isempty(a), error('no measurement angles'), end
la=length(a); sa=size(a); 
if prod(sa)~=la, error('a must be a vector'); end
if (nargin<4) || isempty(ntype), ntype='F'; end
if ~sum(ntype==['F' 'R']), error('ntype must be F or R'), end
if (nargin<3) || isempty(hp), hp=pi; end
if (nargin<2) || isempty(w), w=1/la+0*a; end
lw=length(w); sw=size(w); 
if prod(sw)~=lw, error('w must be a vector'); end
if lw~=la, error('length of w must equal length of a'), end
if sum(w)~=1, warning('resumming weights to unity'), w=w/sum(w); end

a=a(:);     % make column vector
w=w(:);     % make column vector
a=mod(a+hp,2*hp)-hp;    % reduce to central period
a=a/hp*pi;              % scale to half period pi
z=exp(i*a); % U(1) elements

% % NOTA BENE:
% % fminbnd can get hung up near the boundaries.
% % If that happens, shift the input angles a
% % forward by one half period, then shift the
% % resulting mean ma back by one half period.
% X=fminbnd(@meritfcn,-pi,pi,[],z,w,ntype);

% % seems to work better
x0=imag(log(sum(w.*z)));
X=fminbnd(@meritfcn,x0-pi,x0+pi,[],z,w,ntype);

% X=real(X);              % truncate some roundoff
X=mod(X+pi,2*pi)-pi;    % reduce to central period
ma=X*hp/pi;             % scale to half period hp

return
%%%%%%

function d2=meritfcn(x,z,w,ntype)
x=exp(i*x);
if ntype=='F'
    y=x-z;
else % ntype=='R'
    y=log(x'*z);
end
d2=y'*diag(w)*y;
return
%%%%%%

% %   test script
% % 
% % NOTA BENE: meanangleoct(a,[],[],'R') will equal mean(a) 
% % when all abs(a-b) < pi/2 for some value b
% % 
% na=3, a=sort(mod(randn(1,na)+1,2)-1)*pi;
% da=diff([a a(1)+2*pi]); [mda,ndx]=min(da);
% a=circshift(a,[0 2-ndx])    % so that diff(a(2:3)) is smallest
% A=exp(i*a), B1=expm(a(1)*[0 -1; 1 0]), 
% B2=expm(a(2)*[0 -1; 1 0]), B3=expm(a(3)*[0 -1; 1 0]),
% masimpl=[angle(mean(exp(i*a))) mean(a)]
% Bsum=B1+B2+B3; BmeanF=Bsum/sqrt(det(Bsum)); 
% % this expression for BmeanR should be correct for ordering of a above
% BmeanR=B1*(B1'*B2*(B2'*B3)^(1/2))^(2/3);
% mamtrx=real([[0 1]*logm(BmeanF)*[1 0]' [0 1]*logm(BmeanR)*[1 0]'])
% manorm=[meanangleoct(a,[],[],'F') meanangleoct(a,[],[],'R')]
% polar(a,1+0*a,'b*'), axis square, hold on
% polar(manorm(1),1,'rs'), polar(manorm(2),1,'gd'), hold off

%     Meanangleoct Version 1.0
%     Copyright (C) 2011 Alphawave Research, [email protected]
%     Released under GNU GPLv3 -- see file COPYING for more info.
%
%     Meanangle is free software: you can redistribute it and/or modify
%     it under the terms of the GNU General Public License as published by
%     the Free Software Foundation, either version 3 of the License, or (at
%     your option) any later version.
%
%     Meanangle is distributed in the hope that it will be useful, but
%     WITHOUT ANY WARRANTY; without even the implied warranty of
%     MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
%     General Public License for more details.
%
%     You should have received a copy of the GNU General Public License
%     along with this program.  If not, see `http://www.gnu.org/licenses/'.

Chinachinaberry

Answer 10

Here is the full solution: (the input is an array of bearing in degrees (0-360)

public static int getAvarageBearing(int[] arr)
{
    double sunSin = 0;
    double sunCos = 0;
    int counter = 0;

    for (double bearing : arr)
    {
        bearing *= Math.PI/180;

        sunSin += Math.sin(bearing);
        sunCos += Math.cos(bearing);
        counter++; 
    }

    int avBearing = INVALID_ANGLE_VALUE;
    if (counter > 0)
    {
        double bearingInRad = Math.atan2(sunSin/counter, sunCos/counter);
        avBearing = (int) (bearingInRad*180f/Math.PI);
        if (avBearing<0)
            avBearing += 360;
    }

    return avBearing;
}

Flash

This problem has baffled me for a while, your solution works (using Arduino, so a few changes to your code but nothing much), I am showing compass reading and taking readings every 50ms and storing into 16 x reading array, which I then use in your function above, issue of 0-360 wrap around solved! thanks :) – Oakley

Answer 11

In english:

1. Make a second data set with all angles shifted by 180.
2. Take the variance of both data sets.
3. Take the average of the data set with the smallest variance.
4. If this average is from the shifted set then shift the answer again by 180.

In python:

A #numpy NX1 array of angles

if np.var(A) < np.var((A-180)%360):
    average = np.average(A)

else:
    average = (np.average((A-180)%360)+180)%360

Belga

This is a great way to achieve the end result without trig functions, it's simple and easy to implement. – Usually

this works for any range of circular data; just shift by half the circular range; great answer! – Anderton

Answer 12

If anyone is looking for a JavaScript solution to this, I've translated the example given in the wikipedia page Mean of circular quantities (which was also referred to in Nick's answer) into JavaScript/NodeJS code, with help from the mathjs library.

If your angles are in degrees:

const maths = require('mathjs');

getAverageDegrees = (array) => {
    let arrayLength = array.length;

    let sinTotal = 0;
    let cosTotal = 0;

    for (let i = 0; i < arrayLength; i++) {
        sinTotal += maths.sin(array[i] * (maths.pi / 180));
        cosTotal += maths.cos(array[i] * (maths.pi / 180));
    }

    let averageDirection = maths.atan(sinTotal / cosTotal) * (180 / maths.pi);

    if (cosTotal < 0) {
        averageDirection += 180;
    } else if (sinTotal < 0) {
        averageDirection += 360;
    }

    return averageDirection;
}

This solution worked really well for me in order to find the average direction from a set of compass directions. I've tested this on a large range of directional data (0-360 degrees) and it seems very robust.

Alternatively, if your angles are in radians:

const maths = require('mathjs');
getAverageRadians = (array) => {
    let arrayLength = array.length;

    let sinTotal = 0;
    let cosTotal = 0;

    for (let i = 0; i < arrayLength; i++) {
        sinTotal += maths.sin(array[i]);
        cosTotal += maths.cos(array[i]);
    }

    let averageDirection = maths.atan(sinTotal / cosTotal);

    if (cosTotal < 0) {
        averageDirection += 180;
    } else if (sinTotal < 0) {
        averageDirection += 360;
    }

    return averageDirection;
}

Hopefully these solutions are helpful to someone facing a similar programming challenge to me.

Rammish

Answer 13

I would go the vector way using complex numbers. My example is in Python, which has built-in complex numbers:

import cmath # complex math

def average_angle(list_of_angles):

    # make a new list of vectors
    vectors= [cmath.rect(1, angle) # length 1 for each vector
        for angle in list_of_angles]

    vector_sum= sum(vectors)

    # no need to average, we don't care for the modulus
    return cmath.phase(vector_sum)

Note that Python does not need to build a temporary new list of vectors, all of the above can be done in one step; I just chose this way to approximate pseudo-code applicable to other languages too.

Viscus

Answer 14

Here's a complete C++ solution:

#include <vector>
#include <cmath>

double dAngleAvg(const vector<double>& angles) {
    auto avgSin = double{ 0.0 };
    auto avgCos = double{ 0.0 };
    static const auto conv      = double{ 0.01745329251994 }; // PI / 180
    static const auto i_conv    = double{ 57.2957795130823 }; // 180 / PI
    for (const auto& theta : angles) {
        avgSin += sin(theta*conv);
        avgCos += cos(theta*conv);
    }
    avgSin /= (double)angles.size();
    avgCos /= (double)angles.size();
    auto ret = double{ 90.0 - atan2(avgCos, avgSin) * i_conv };
    if (ret<0.0) ret += 360.0;
    return fmod(ret, 360.0);
}

It takes the angles in the form of a vector of doubles, and returns the average simply as a double. The angles must be in degrees, and of course the average is in degrees as well.

Charlot

avgCos is the average of the x components, and avgSin is the average of the y components. The parameters for the arctangent function are atan2( y, x ). So, shouldn't your code instead be: atan2( avgSin, avgCos ) ?? – Metaplasm

I got this algorithm from somewhere, I didn't come up with it myself, so I assume it's correct the way it is. Plus it gives correct results as well. – Charlot

Answer 15

Based on Alnitak's answer, I've written a Java method for calculating the average of multiple angles:

If your angles are in radians:

public static double averageAngleRadians(double... angles) {
    double x = 0;
    double y = 0;
    for (double a : angles) {
        x += Math.cos(a);
        y += Math.sin(a);
    }

    return Math.atan2(y, x);
}

If your angles are in degrees:

public static double averageAngleDegrees(double... angles) {
    double x = 0;
    double y = 0;
    for (double a : angles) {
        x += Math.cos(Math.toRadians(a));
        y += Math.sin(Math.toRadians(a));
    }

    return Math.toDegrees(Math.atan2(y, x));
}

Suppurative

Answer 16

Here's an idea: build the average iteratively by always calculating the average of the angles that are closest together, keeping a weight.

Another idea: find the largest gap between the given angles. Find the point that bisects it, and then pick the opposite point on the circle as the reference zero to calculate the average from.

Peltate

I don't recommend my answer, but instead starblue's highly ranked answer. The key observation there is to think of the center of the compass as the 0,0 point. – Peltate

Answer 17

Let's represent these angles with points on the circumference of the circle.

Can we assume that all these points fall on the same half of the circle? (Otherwise, there is no obvious way to define the "average angle". Think of two points on the diameter, e.g. 0 deg and 180 deg --- is the average 90 deg or 270 deg? What happens when we have 3 or more evenly spread out points?)

With this assumption, we pick an arbitrary point on that semicircle as the "origin", and measure the given set of angles with respect to this origin (call this the "relative angle"). Note that the relative angle has an absolute value strictly less than 180 deg. Finally, take the mean of these relative angles to get the desired average angle (relative to our origin of course).

Honan

Answer 18

There's no single "right answer". I recommend reading the book, K. V. Mardia and P. E. Jupp, "Directional Statistics", (Wiley, 1999), for a thorough analysis.

Unhappy

Answer 19

(Just want to share my viewpoint from Estimation Theory or Statistical Inference)

Nimble's trial is to get the MMSE^ estimate of a set of angles, but it's one of choices to find an "averaged" direction; one can also find an MMAE^ estimate, or some other estimate to be the "averaged" direction, and it depends on your metric quantifying error of direction; or more generally in estimation theory, the definition of cost function.

^ MMSE/MMAE corresponds to minimum mean squared/absolute error.

ackb said "The average angle phi_avg should have the property that sum_i|phi_avg-phi_i|^2 becomes minimal...they average something, but not angles"

---- you quantify errors in mean-squared sense and it's one of the mostly common way, however, not the only way. The answer favored by most people here (i.e., sum of the unit vectors and get the angle of the result) is actually one of the reasonable solutions. It is (can be proved) the ML estimator that serves as the "averaged" direction we want, if the directions of the vectors are modeled as von Mises distribution. This distribution is not fancy, and is just a periodically sampled distribution from a 2D Guassian. See Eqn. (2.179) in Bishop's book "Pattern Recognition and Machine Learning". Again, by no means it's the only best one to represent "average" direction, however, it is quite reasonable one that have both good theoretical justification and simple implementation.

Nimble said "ackb is right that these vector based solutions cannot be considered true averages of angles, they are only an average of the unit vector counterparts"

----this is not true. The "unit vector counterparts" reveals the information of the direction of a vector. The angle is a quantity without considering the length of the vector, and the unit vector is something with additional information that the length is 1. You can define your "unit" vector to be of length 2, it does not really matter.

Cameral

Answer 20

You can see a solution and a little explanation in the following link, for ANY programming language: https://rosettacode.org/wiki/Averages/Mean_angle

For instance, C++ solution:

#include<math.h>
#include<stdio.h>

double
meanAngle (double *angles, int size)
{
  double y_part = 0, x_part = 0;
  int i;

  for (i = 0; i < size; i++)
    {
      x_part += cos (angles[i] * M_PI / 180);
      y_part += sin (angles[i] * M_PI / 180);
    }

  return atan2 (y_part / size, x_part / size) * 180 / M_PI;
}

int
main ()
{
  double angleSet1[] = { 350, 10 };
  double angleSet2[] = { 90, 180, 270, 360};
  double angleSet3[] = { 10, 20, 30};

  printf ("\nMean Angle for 1st set : %lf degrees", meanAngle (angleSet1, 2));
  printf ("\nMean Angle for 2nd set : %lf degrees", meanAngle (angleSet2, 4));
  printf ("\nMean Angle for 3rd set : %lf degrees\n", meanAngle (angleSet3, 3));
  return 0;
}

Output:

Mean Angle for 1st set : -0.000000 degrees
Mean Angle for 2nd set : -90.000000 degrees
Mean Angle for 3rd set : 20.000000 degrees

Or Matlab solution:

function u = mean_angle(phi)
    u = angle(mean(exp(i*pi*phi/180)))*180/pi;
end

 mean_angle([350, 10])
ans = -2.7452e-14
 mean_angle([90, 180, 270, 360])
ans = -90
 mean_angle([10, 20, 30])
ans =  20.000

Vexed

Answer 21

Here is a completely arithmetic solution using moving averages and taking care to normalize values. It is fast and delivers correct answers if all angles are on one side of the circle (within 180° of each other).

It is mathimatically equivalent to adding the offset which shifts the values into the range (0, 180), calulating the mean and then subtracting the offset.

The comments describe what range a specific value can take on at any given time

// angles have to be in the range [0, 360) and within 180° of each other.
// n >= 1
// returns the circular average of the angles int the range [0, 360).
double meanAngle(double* angles, int n)
{
    double average = angles[0];
    for (int i = 1; i<n; i++)
    {
        // average: (0, 360)
        double diff = angles[i]-average;
        // diff: (-540, 540)

        if (diff < -180)
            diff += 360;
        else if (diff >= 180)
            diff -= 360;
        // diff: (-180, 180)

        average += diff/(i+1);
        // average: (-180, 540)

        if (average < 0)
            average += 360;
        else if (average >= 360)
            average -= 360;
        // average: (0, 360)
    }
    return average;
}

Temporize

Answer 22

Well I'm hugely late to the party but thought I'd add my 2 cents worth as I couldn't really find any definitive answer. In the end I implemented the following Java version of the Mitsuta method which, I hope, provides a simple and robust solution. Particularly as the Standard Deviation provides both a measure dispersion and, if sd == 90, indicates that the input angles result in an ambiguous mean.

EDIT: Actually I realised that my original implementation can be even further simplified, in fact worryingly simple considering all the conversation and trigonometry going on in the other answers.

/**
 * The Mitsuta method
 *
 * @param angles Angles from 0 - 360
 * @return double array containing
 * 0 - mean
 * 1 - sd: a measure of angular dispersion, in the range [0..360], similar to standard deviation.
 * Note if sd == 90 then the mean can also be its inverse, i.e. 360 == 0, 300 == 60.
 */
public static double[] getAngleStatsMitsuta(double... angles) {
    double sum = 0;
    double sumsq = 0;
    for (double angle : angles) {
        if (angle >= 180) {
            angle -= 360;
        }
        sum += angle;
        sumsq += angle * angle;
    }

    double mean = sum / angles.length;
    return new double[]{mean <= 0 ? 360 + mean: mean, Math.sqrt(sumsq / angles.length - (mean * mean))};
}

... and for all you (Java) geeks out there, you can use the above approach to get the mean angle in one line.

Arrays.stream(angles).map(angle -> angle<180 ? angle: (angle-360)).sum() / angles.length;

Area

I believe you missed something out of the Mitsuda method. Please take a look at the answer posted by Lior Kogan https://mcmap.net/q/138299/-averaging-angles-again – Affectation

Answer 23

Alnitak has the right solution. Nick Fortescue's solution is functionally the same.

For the special case of where

( sum(x_component) = 0.0 && sum(y_component) = 0.0 ) // e.g. 2 angles of 10. and 190. degrees ea.

use 0.0 degrees as the sum

Computationally you have to test for this case since atan2(0. , 0.) is undefined and will generate an error.

Sleight

on glibc 'atan2' is defined for (0, 0) - the result is 0 – Dzerzhinsk

Answer 24

The average angle phi_avg should have the property that sum_i|phi_avg-phi_i|^2 becomes minimal, where the difference has to be in [-Pi, Pi) (because it might be shorter to go the other way around!). This is easily achieved by normalizing all input values to [0, 2Pi), keeping a running average phi_run and choosing normalizing |phi_i-phi_run| to [-Pi,Pi) (by adding or subtractin 2Pi). Most suggestions above do something else that does not have that minimal property, i.e., they average something, but not angles.

Igraine

Answer 25

Python function:

from math import sin,cos,atan2,pi
import numpy as np
def meanangle(angles,weights=0,setting='degrees'):
    '''computes the mean angle'''
    if weights==0:
         weights=np.ones(len(angles))
    sumsin=0
    sumcos=0
    if setting=='degrees':
        angles=np.array(angles)*pi/180
    for i in range(len(angles)):
        sumsin+=weights[i]/sum(weights)*sin(angles[i])
        sumcos+=weights[i]/sum(weights)*cos(angles[i])
    average=atan2(sumsin,sumcos)
    if setting=='degrees':
        average=average*180/pi
    return average

Nun

Answer 26

You can use this function in Matlab:

function retVal=DegreeAngleMean(x) 

len=length(x);

sum1=0; 
sum2=0; 

count1=0;
count2=0; 

for i=1:len 
   if x(i)<180 
       sum1=sum1+x(i); 
       count1=count1+1; 
   else 
       sum2=sum2+x(i); 
       count2=count2+1; 
   end 
end 

if (count1>0) 
     k1=sum1/count1; 
end 

if (count2>0) 
     k2=sum2/count2; 
end 

if count1>0 && count2>0 
   if(k2-k1 >= 180) 
       retVal = ((sum1+sum2)-count2*360)/len; 
   else 
       retVal = (sum1+sum2)/len; 
   end 
elseif count1>0 
    retVal = k1; 
else 
    retVal = k2; 
end 

Microdont

The algorithm just appears to work, but in reality it might fail miserably in real world. Giving you angle values that are in the opposite direction of the given angles. – Cock

Answer 27

While starblue's answer gives the angle of the average unit vector, it is possible to extend the concept of the arithmetic mean to angles if you accept that there may be more than one answer in the range of 0 to 2*pi (or 0° to 360°). For example, the average of 0° and 180° may be either 90° or 270°.

The arithmetic mean has the property of being the single value with the minimum sum of squared distances to the input values. The distance along the unit circle between two unit vectors can be easily calculated as the inverse cosine of their dot product. If we choose a unit vector by minimizing the sum of the squared inverse cosine of the dot product of our vector and each input unit vector then we have an equivalent average. Again, keep in mind that there may be two or more minimums in exceptional cases.

This concept could be extended to any number of dimensions, since the distance along the unit sphere can be calculated in the exact same way as the distance along the unit circle--the inverse cosine of the dot product of two unit vectors.

For circles we could solve for this average in a number of ways, but I propose the following O(n^2) algorithm (angles are in radians, and I avoid calculating the unit vectors):

var bestAverage = -1
double minimumSquareDistance
for each a1 in input
    var sumA = 0;
    for each a2 in input
        var a = (a2 - a1) mod (2*pi) + a1
        sumA += a
    end for
    var averageHere = sumA / input.count
    var sumSqDistHere = 0
    for each a2 in input
        var dist = (a2 - averageHere + pi) mod (2*pi) - pi // keep within range of -pi to pi
        sumSqDistHere += dist * dist
    end for
    if (bestAverage < 0 OR sumSqDistHere < minimumSquareDistance) // for exceptional cases, sumSqDistHere may be equal to minimumSquareDistance at least once. In these cases we will only find one of the averages
        minimumSquareDistance = sumSqDistHere
        bestAverage = averageHere
    end if
end for
return bestAverage

If all the angles are within 180° of each other, then we could use a simpler O(n)+O(sort) algorithm (again using radians and avoiding use of unit vectors):

sort(input)
var largestGapEnd = input[0]
var largestGapSize = (input[0] - input[input.count-1]) mod (2*pi)
for (int i = 1; i < input.count; ++i)
    var gapSize = (input[i] - input[i - 1]) mod (2*pi)
    if (largestGapEnd < 0 OR gapSize > largestGapSize)
        largestGapSize = gapSize
        largestGapEnd = input[i]
    end if
end for
double sum = 0
for each angle in input
    var a2 = (angle - largestGapEnd) mod (2*pi) + largestGapEnd
    sum += a2
end for
return sum / input.count

To use degrees, simply replace pi with 180. If you plan to use more dimensions then you will most likely have to use an iterative method to solve for the average.

Shrub

Answer 28

The problem is extremely simple. 1. Make sure all angles are between -180 and 180 degrees. 2. a Add all non-negative angles, take their average, and COUNT how many 2. b.Add all negative angles, take their average and COUNT how many. 3. Take the difference of pos_average minus neg_average If difference is greater than 180 then change difference to 360 minus difference. Otherwise just change the sign of difference. Note that difference is always non-negative. The Average_Angle equals the pos_average plus difference times the "weight", negative count divided by the sum of negative and positive count

Gramarye

Answer 29

Here is some java code to average angles, I think it's reasonably robust.

public static double getAverageAngle(List<Double> angles)
{
    // r = right (0 to 180 degrees)

    // l = left (180 to 360 degrees)

    double rTotal = 0;
    double lTotal = 0;
    double rCtr = 0;
    double lCtr = 0;

    for (Double angle : angles)
    {
        double norm = normalize(angle);
        if (norm >= 180)
        {
            lTotal += norm;
            lCtr++;
        } else
        {
            rTotal += norm;
            rCtr++;
        }
    }

    double rAvg = rTotal / Math.max(rCtr, 1.0);
    double lAvg = lTotal / Math.max(lCtr, 1.0);

    if (rAvg > lAvg + 180)
    {
        lAvg += 360;
    }
    if (lAvg > rAvg + 180)
    {
        rAvg += 360;
    }

    double rPortion = rAvg * (rCtr / (rCtr + lCtr));
    double lPortion = lAvg * (lCtr / (lCtr + rCtr));
    return normalize(rPortion + lPortion);
}

public static double normalize(double angle)
{
    double result = angle;
    if (angle >= 360)
    {
        result = angle % 360;
    }
    if (angle < 0)
    {
        result = 360 + (angle % 360);
    }
    return result;
}

Collete

Answer 30

I solved the problem with the help of the answer from @David_Hanak. As he states:

The angle that points "between" the two others while staying in the same semicircle, e.g. for 355 and 5, this would be 0, not 180. To do this, you need to check if the difference between the two angles is larger than 180 or not. If so, increment the smaller angle by 360 before using the above formula.

So what I did was calculate the average of all the angles. And then all the angles that are less than this, increase them by 360. Then recalculate the average by adding them all and dividing them by their length.

        float angleY = 0f;
        int count = eulerAngles.Count;

        for (byte i = 0; i < count; i++)
            angleY += eulerAngles[i].y;

        float averageAngle = angleY / count;

        angleY = 0f;
        for (byte i = 0; i < count; i++)
        {
            float angle = eulerAngles[i].y;
            if (angle < averageAngle)
                angle += 360f;
            angleY += angle;
        }

        angleY = angleY / count;

Works perfectly.

Salisbury

Answer 31

I have a different method than @Starblue that gives "correct" answers to some of the angles given above. For example:

• angle_avg([350,10])=0
• angle_avg([-90,90,40])=13.333
• angle_avg([350,2])=356

It uses a sum over the differences between consecutive angles. The code (in Matlab):

function [avg] = angle_avg(angles)
last = angles(1);
sum = angles(1);
for i=2:length(angles)
    diff = mod(angles(i)-angles(i-1)+ 180,360)-180
    last = last + diff;
    sum = sum + last;
end
avg = mod(sum/length(angles), 360);
end

Ballentine

Your code returns different answers for [-90,90,40] and [90,-90,40]; I don't think a non-commutative average is a very useful one. – Jainism