Piecewise linear fit with n breakpoints

Question

I have used some code found in the question How to apply piecewise linear fit in Python?, to perform segmented linear approximation with a single breakpoint.

The code is as follows:

from scipy import optimize
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12, 13, 14, 15], dtype=float)
y = np.array([5, 7, 9, 11, 13, 15, 28.92, 42.81, 56.7, 70.59, 84.47, 98.36, 112.25, 126.14, 140.03])

def piecewise_linear(x, x0, y0, k1, k2):
    return np.piecewise(x, 
                       [x < x0], 
                       [lambda x:k1*x + y0-k1*x0, lambda x:k2*x + y0-k2*x0])

p , e = optimize.curve_fit(piecewise_linear, x, y)
xd = np.linspace(0, 15, 100)
plt.plot(x, y, "o")
plt.plot(xd, piecewise_linear(xd, *p))

I am trying to figure out how I can extend this to handle n breakpoints.

I tried the following code for the piecewise_linear() method to handle 2 breakpoints, but it does not alter the values of the breakpoints in any way.

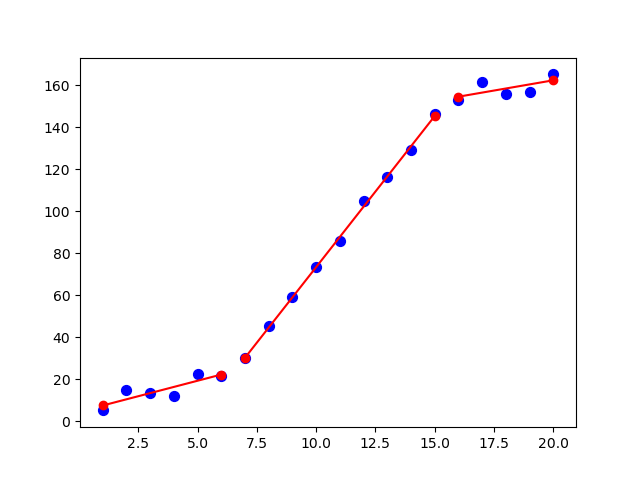
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20], dtype=float)
y = np.array([5, 7, 9, 11, 13, 15, 28.92, 42.81, 56.7, 70.59, 84.47, 98.36, 112.25, 126.14, 140.03, 150, 152, 154, 156, 158])

def piecewise_linear(x, x0, x1, a1, b1, a2, b2, a3, b3):
    return np.piecewise(x,
                       [x < x0, np.logical_and(x >= x0, x < x1), x >= x1 ], 
                       [lambda x:a1*x + b1, lambda x:a2*x+b2, lambda x: a3*x + b3])

p , e = optimize.curve_fit(piecewise_linear, x, y)
xd = np.linspace(0, 20, 100)
plt.plot(x, y, "o")
plt.plot(xd, piecewise_linear(xd, *p))

Any input would be greatly appreciated

Andromada

It does not work is a pretty much useless description. I also think you won't achieve that with curve_fit(), which gets more complex when there are multiple breakpoints (would need linear-constraints to handle b0 < b1; not supported; ignoring this and sorting before np.piecewise touches the last argument here). It's also a non-convex optimization problem and therefore all those optimizers available in scipy only achieve a local-minimum (if they achieve that at all). That being said, i also doubt the effectiveness of the one-breakpoint approach using curve-fit (as it's non-smooth). – Bose

I think that if I initially distribute the breakpoints uniformly across the x-axis then finding local-minimums will be sufficient to provide a decent non-optimal solution. Do you know of another optimization module which does support linear constraints? – Andromada

As i told you, it's not just about that. Ignoring smoothness and potential non-convexity, you can solve this problem with scipy's more general optimize functions, namely COBYLA and SQSLP (the only two supporting constraints). The only real approach i see would be mixed-integer convex-programming, but software is sparse (bonmin and couenne being two open-source solvers not that nice to use from python; pajarito @ julialang; but this approach in general needs some non-trivial formulation). – Bose

Answer 1

NumPy has a polyfit function which makes it very easy to find the best fit line through a set of points:

coefs = npoly.polyfit(xi, yi, 1)

So really the only difficulty is finding the breakpoints. For a given set of breakpoints it's trivial to find the best fit lines through the given data.

So instead of trying to find location of the breakpoints and the coefficients of the linear parts all at once, it suffices to minimize over a parameter space of breakpoints.

Since the breakpoints can be specified by their integer index values into the x array, the parameter space can be thought of as points on an integer grid of N dimensions, where N is the number of breakpoints.

optimize.curve_fit is not a good choice as the minimizer for this problem because the parameter space is integer-valued. If you were to use curve_fit, the algorithm would tweak the parameters to determine in which direction to move. If the tweak is less than 1 unit, the x-values of the breakpoints do not change, so the error does not change, so the algorithm gains no information about the correct direction in which to shift the parameters. Hence curve_fit tends to fail when the parameter space is essentially integer-valued.

A better, but not very fast, minimizer would be a brute-force grid search. If the number of breakpoints is small (and the parameter space of x-values is small) this might suffice. If the number of breakpoints is large and/or the parameter space is large, then perhaps set up a multi-stage coarse/fine (brute-force) grid search. Or, perhaps someone will suggest a smarter minimizer than brute-force...

---

import numpy as np
import numpy.polynomial.polynomial as npoly
from scipy import optimize
import matplotlib.pyplot as plt
np.random.seed(2017)

def f(breakpoints, x, y, fcache):
    breakpoints = tuple(map(int, sorted(breakpoints)))
    if breakpoints not in fcache:
        total_error = 0
        for f, xi, yi in find_best_piecewise_polynomial(breakpoints, x, y):
            total_error += ((f(xi) - yi)**2).sum()
        fcache[breakpoints] = total_error
    # print('{} --> {}'.format(breakpoints, fcache[breakpoints]))
    return fcache[breakpoints]

def find_best_piecewise_polynomial(breakpoints, x, y):
    breakpoints = tuple(map(int, sorted(breakpoints)))
    xs = np.split(x, breakpoints)
    ys = np.split(y, breakpoints)
    result = []
    for xi, yi in zip(xs, ys):
        if len(xi) < 2: continue
        coefs = npoly.polyfit(xi, yi, 1)
        f = npoly.Polynomial(coefs)
        result.append([f, xi, yi])
    return result

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 
              18, 19, 20], dtype=float)
y = np.array([5, 7, 9, 11, 13, 15, 28.92, 42.81, 56.7, 70.59, 84.47, 98.36, 112.25, 
              126.14, 140.03, 150, 152, 154, 156, 158])
# Add some noise to make it exciting :)
y += np.random.random(len(y))*10

num_breakpoints = 2
breakpoints = optimize.brute(
    f, [slice(1, len(x), 1)]*num_breakpoints, args=(x, y, {}), finish=None)

plt.scatter(x, y, c='blue', s=50)
for f, xi, yi in find_best_piecewise_polynomial(breakpoints, x, y):
    x_interval = np.array([xi.min(), xi.max()])
    print('y = {:35s}, if x in [{}, {}]'.format(str(f), *x_interval))
    plt.plot(x_interval, f(x_interval), 'ro-')


plt.show()

prints

y = poly([ 4.58801083  2.94476604])    , if x in [1.0, 6.0]
y = poly([-70.36472935  14.37305793])  , if x in [7.0, 15.0]
y = poly([ 123.24565235    1.94982153]), if x in [16.0, 20.0]

and plots

Litigious

Great answer... I tried everything I could with leastsq and minimize but the piecewise parameters x0 and x1 are just not optimized correctly – Phonics

Perfect. Thank you! – Andromada

How would one change this to allow for curve_fit to work (and assuming the data is not strictly integer-spaced)? – Bonnee

Also, what is fcache representing here? – Bonnee

@genjong: fcache is a memoizer. It is a dict which maps pairs of breakpoints to the corresponding total error. f can be called more than once with the same breakpoints. fcache makes f more efficient by simply returning the memoized total error instead of computing the same thing twice. You can see it in action by uncommenting the print statement in f. – Litigious

@genjong: To apply curve_fit, you would first need to define a function similar to f which maps continuous-valued breakpoints to a measure of total_error. Once you have such an f, applying curve_fit is in theory straight-forward, just like any other application of curve_fit. – Litigious

Note that successful use of curve_fit generally requires f to be reasonably smooth but also have enough variation to allow the gradient to point in the direction of the minimum. If you modify f to simply "snap" continuous-valued breakpoints to the nearest integer, then f will be locally flat, so the optimizer will not be able to find a minimum because the gradient will be zero in all directions. – Litigious