Tail Call Optimisation in R creates a new environment for every function call
Tail call optimisation (TCO) in R using Tailcall() allows recursive functions to avoid stack overflows by unwinding the call stack and starting from the global environment for each recursive call. However, unlike TCO in some other languages, R's implementation does not reuse the same stack frame or rewrite the recursion as a loop. It still calls the recursive function (and creates a new environment) the same number of times. This means that while Tailcall() prevents the stack overflow depth increasing every time, it may not significantly improve performance. In fact, the overhead associated with implementing Tailcall() means that it appears to be slower than a standard recursive function.
Benchmarking Tailcall()
Here's an R equivalent of the recursive sum functions in the JavaScript answer to What is tail recursion? that we can call thousands of times recursively.
# Without tail recursion
recsum <- function(x) {
if (x == 0) {
return(0)
} else {
force(x) # to make benchmark fair
return(x + recsum(x - 1))
}
}
# With tail recursion
tailrecsum <- function(x, running_total = 0) {
if (x == 0) {
return(running_total)
} else {
force(running_total) # you have to force evaluation to trigger tail recursion
Tailcall(tailrecsum, x - 1, running_total + x)
}
}
To increase maximum recursion depth for the benchmark, this is an R session started with R --max-ppsize=500000
options(expressions = 5e5) # max recursion depth option
bench::mark(recsum(4e3), tailrecsum(4e3), relative = TRUE)
# expression min median `itr/sec` mem_alloc `gc/sec` n_itr n_gc total_time
# <bch:expr> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <bch:tm>
# 1 recsum(4000) 1 1 2.11 NaN 1 469 27 427ms
# 2 tailrecsum(4000) 2.20 2.13 1 Inf 1.16 206 29 396ms
Even with a depth of 4001 (which is about the most that R will let recsum() do), the TCO version is still about twice as slow. What's going on? The key is on the Tailcall() help page:
[S]tack traces produced by traceback or sys.calls will only show the call specified by Tailcall or Exec, not the previous call whose stack entry has been replaced.
(Emphasis mine.)
The process is something like this:
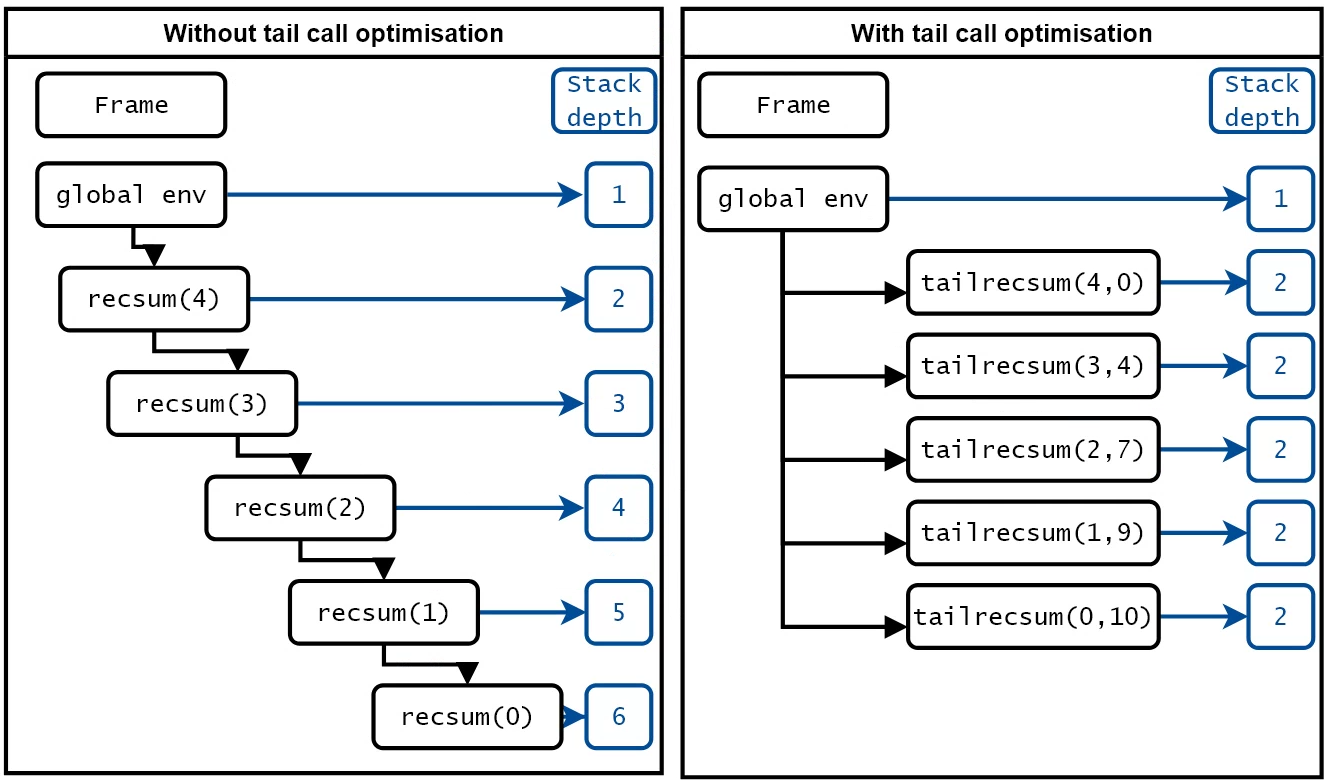
![image of stack frame usage]()
The key point of this image is that while with Tailcall() the stack does not grow for each additional function call, R does not reuse the same stack frame for each call. It unwinds the stack and creates a new environment each time it calls tailrecsum(), which happens the same number of times as recsum() would be called. To understand this difference, let's look at a comparison in C.
How does gcc do TCO?
Let's write tailrecsum() in C:
uint64_t tailrecsum(uint64_t x, uint64_t running_total) {
if (x == 0) {
return running_total;
} else {
return tailrecsum(x - 1, running_total + x);
}
}
If we compile it and disable optimisation with gcc -O0 the assembly will include a recursive call, i.e.:
tailrecsum:
push rbp
; <some other instructions>
call tailrecsum
However, if we compile it with O2 optimisation, the assembly looks very different:
tailrecsum:
mov rax, rsi ; move 'running_total' into 'rax' (accumulator)
test rdi, rdi ; test if 'x' == 0
je .L5 ; if 'x' == 0, jump to .L5 (base case)
lea rdx, [rdi - 1] ; calculate x - 1 and store it in rdx for later use.
test dil, 1 ; test if the least significant bit of 'x' is 1 (odd or even)
je .L2 ; if even, jump to label .L2
add rax, rdi ; rax += x (accumulate the sum)
mov rdi, rdx ; x = x - 1
test rdx, rdx ; test if x == 0
je .L17 ; if x == 0, jump to label .L17 to return
; Fall through to .L2
.L2:
lea rax, [rax - 1 + rdi * 2] ; rax = rax - 1 + 2 * x
sub rdi, 2 ; x = x - 2
jne .L2 ; if x != 0, jump back to .L2 (loop)
; If x == 0, fall through to .L5
.L5:
ret ; return from function
.L17:
ret ; return from function
There is no recursive call. The compiler has transformed the code into a loop. The function does not call itself, so only one stack frame is used.
R's TCO does not optimise a recursive function into a loop
Conversely, even with Tailcall(), R creates a new stack frame every function call. We can observe this by writing a TCO function which counts the number of environments:
tailrecsumenv <- function(x, running_total = 0, env_list) {
if (x == 0) {
return(
list(
result = running_total,
n_environments = length(unique(env_list))
)
)
} else {
force(running_total) # force evaluation to trigger TCO
force(env_list)
Tailcall(tailrecsumenv, x - 1, running_total + x, append(env_list, environment()))
}
}
If we run this we can see it creates 4001 environments:
tailrecsumenv(4e3, env_list = list(environment()))
# $result
# [1] 8002000
# $n_environments
# [1] 4001
So how does Tailcall() work in R?
The R source shows the checks that it does when you use Tailcall() :
Rboolean jump_OK =
(R_GlobalContext->conexit == R_NilValue &&
R_GlobalContext->callflag & CTXT_FUNCTION &&
R_GlobalContext->cloenv == rho &&
TYPEOF(R_GlobalContext->callfun) == CLOSXP &&
checkTailPosition(call, BODY_EXPR(R_GlobalContext->callfun), rho));
It checks that there are no pending on.exit expressions, the current context is a function, the closure environment matches, the function being called is a closure and that the call is in tail position. These checks will have some overhead. For example, checking tail position will require traversing the abstract syntax tree. If TCO can be applied, it does the following (slightly simplified and with my comments):
if (jump_OK) {
// construct the first argument of `Tailcall()` into a function call
SEXP fun = CAR(expr);
// ensure function can be properly resolved
fun = eval(fun, env);
// package the function into a list containing...
SEXP val = allocVector(VECSXP, 4);
SET_VECTOR_ELT(val, 0, R_exec_token); // an execution token
SET_VECTOR_ELT(val, 1, expr); // the expression to evaluate
SET_VECTOR_ELT(val, 2, env); // the environment in which to evaluate it
SET_VECTOR_ELT(val, 3, fun); // the function to call
// Jump back to the global environment
R_jumpctxt(R_GlobalContext, CTXT_FUNCTION, val);
}
The crucial part is R_jumpctxt(). What this effectively does is unwind the stack to the global environment, and replace the current function call with a new one. This means it is possible to call another function without increasing the call stack depth. However, unlike TCO in the C example, each recursive call with Tailcall() results in a new environment being created.
This is equivalent to returning from the top-level function before calling the recursive function. It allows deep recursion without exceeding the maximum stack size. However, you do not get the same types of optimisation that you see in the C code. A new environment needs to be created, which is a relatively expensive operation. These environments consume memory on the heap, not the call stack, but they are not immediately reused or deleted. They will continue to grow memory and will persist until garbage collected.
Comparing the call stack trees
We can see this if we stick lobstr::cst() in the if (x == 0) branch of our function to print the call stack trees before they return the answer. Without Tailcall() we get the correct stack trace:
recsum(5)
▆
1. └─global recsum(5)
2. └─global recsum(x - 1)
3. └─global recsum(x - 1)
4. └─global recsum(x - 1)
5. └─global recsum(x - 1)
6. └─global recsum(x - 1)
7. └─lobstr::cst()
[1] 15
However, with Tailcall(), R thinks that the final function has been called from the global environment, and doesn't know about the previous calls:
tailrecsum(5)
▆
1. └─global tailrecsum(x - 1, running_total + x)
2. └─lobstr::cst()
[1] 15
This is noted in the docs:
[S]tack traces... will only show the call specified by Tailcall or Exec, not the previous call whose stack entry has been replaced
So if Tailcall() is slower, what is the point?
In fairness, the docs never claim that Tailcall() is faster:
This tail call optimization has the advantage of not growing the call stack and permitting arbitrarily deep tail recursions.
While recsum() and tailrecsum() are a ridiculous way to calculate sum(1:4e3) in a language like R, the advantage of Tailcall() is that it does prevent stack overflow caused by deep recursion:
recsum(1e6)
# Error in force(x) : node stack overflow
tailrecsum(1e6)
# [1] 500000500000
Tailcall() is an optimisation in that it allows code to be run that otherwise could not be. But it does not generate the types of efficiencies seen in other languages using TCO. R still has to create environments in the same way as it would with a recursive function. It also has additional work, as running Tailcall() requires parsing the code to assess whether TCO is appropriate, then unwinding the call stack before making the next recursive call. So while Tailcall() prevents the call stack from growing indefinitely, don't expect it to be faster than a standard recursive function that does not cause a stack overflow. It probably won't be.

bisect <- function(l, u, counter = 1)and then set subsequent calls to increment the counter, e.g.bisect(l, mid, counter + 1), you'll see it only has 48 iterations. If you use a smaller tolerance to force more iterations you might see the benefit (and at some point you won't be able to run the original function). Also I would see ifcompiler::cpmfun()makes a difference. – Ambsace1e-15tolerance is already the minimum (a smaller value would be below what R can represent numerically, so theu - lcould never be smaller). Regarding your second idea, thanks for the suggestion, I update the question with an answer to that. – ForenamedTailcall()first and foremost helps ensure that it will run for large inputs without crashing, nothing more. Now, it would be great if it didn’t slow down existing code (in fact, I’d consider the current state a QoI/performance bug). – SplasherTailcall()makes the code slower although I haven't used it in a real example so I'm not sure whether the speed difference is actually noticeable. I think the docs could perhaps be a little more explicit but it is apparently experimental at the moment. – Ambsace