Marching Cubes, voxels, need a bit of suggestions

Question

I'm trying to construct a proper destructible terrain, just for research purposes. Well, everything went fine, but resolution is not satisfying me enough. I have seen a lot of examples how people implement MC algorithm, but most of them, as far as I understand, uses functions to triangulate final mesh, which is not appropriate for me.

I will try briefly to explain how I'm constructing my terrain, and maybe someone of you will give me suggestion how to improve, or to increase resolution of final terrain.

1) Precalculating MC triangles.

I'm running simple loop through MC lookup tables for each case(0-255) and calculating triangles in rage: [0,0,0] - [1,1,1]. No problems here.

2) Terrain

I have terrain class, which stores my voxels. In general, it looks like this:

int size = 32;//Size of each axis.
unsigned char *voxels = new unsigned char[(size * size * size)/8];

So, each axis is 32 units of size long, but, I store voxel information per bit. Meaning if bit is turned on (1), there is something, and there should be draw something.

I have couple of functions:

TurnOn(x,y,z);
TurnOff(x,y,z);

to turn location of voxel on or off. (Helps to work with bits).

Once terrain is allocated, I'm running perlin noise, and turning bits on or off.

My terrain class has one more function, to extract Marching Cubes case number (0-255) from x,y,z location:

unsigned char GetCaseNumber(x,y,z);

by determining if neighbours of that voxel is turned on or off. No problems here.

3) Rendering part

I'm looping for each axis, extracting case number, then getting precalculated triangles by case, translating to x,y,z coordinates, and drawing those triangles. no problems here.

So result looks like this:

But as you can see, in any single location, resolution is not comparable to for example this:
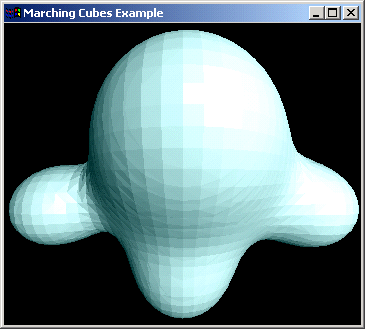
_{(source: angelfire.com)}

I have seen in MC examples that people are using something called "iso values", which I don't understand. Any suggestions how to improve my work, or what is iso values, and how to implement it in uniform grid would be truly lovely.

Bamboo

resolution looks the same to me, except the sample doesn't appear locked to a grid like yours appears to be. – Nitroglycerin

I think you meant "isometric surfaces". The idea is taking some scalar field function, e.g. a sphere r(x,y,z) = sqrt(x**2 + y**2 + z**2) and testing for some threshold value to decide if the position is inside or outside the defined threshold. In your MC implementation you'd use the result of r(x,y,z) > t instead of the voxel filling bit. – Aleppo

Answer 1

The problem is that your voxels are a binary mask (just on or off).

This is great for the "default" marching cubes algorithm, but it it does mean you get sharp edges in your mesh.

The smooth example is probably generated from smooth scalar data.

Imagine that if your data varies smoothly between 0 and 1.0, and you set your threshold to 0.5. Now, after you detect which configuration a given cube is, you look at the all the vertices generated.

Say, that you have a vertex on an edge between two voxels, one with value 0.4 and the other 0.7. Then you move the vertex to the position where you would get exactly 0.5 (the threshold) when interpolating between 0.4 and 0.7. So it will be closer to the 0.4 vertex.

This way, each vertex is exactly on the interpolated iso surface and you will generate much smoother triangles.

But it does require that your input voxels are scalar (and vary smoothly). If your voxels are bi-level (all either 0 or 1), this will produce the same triangles as you got earlier.

Another idea (not the answer to your question but perhaps useful):

To just get smoother rendering, without mathematical correctness, it could be worthwile to compute an average normal vector for each vertex, and use that normal for each triangle connecting to it. This will hide the sharp edges.

Perfume