3D Surface with Plot_ly in r, with x,y,z coordinates

Question

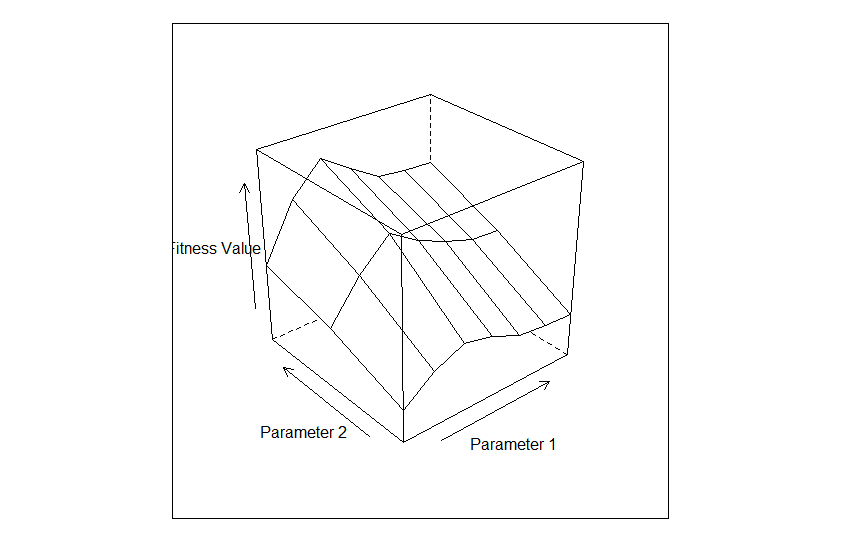
I am trying to use 3D surface plots to analyze the stability of outcomes as a function of inputs. z is my outcome, and x and y are parameter values. Using lattice's wireframe I can make a surface plot no problem, but it would be nice to have the interactive and sharable capabilities of plotly. The volcano example doesn't show how to take x,y,z coordinates and make a surface plot. Anyone know how to concisely do that? Here is the lattice wireframe example and data:

library(lattice) 

z <- c(0.035, 0.043, 0.036, 0.037, 0.016, 0.013, 0.025, 0.037, 0.039, 0.043,         
0.049, 0.029, 0.025, 0.02,  0.032, 0.045, 0.049, 0.043, 0.027, 0.031, 
0.028,0.039, 0.038, 0.037, 0.045, 0.046, 0.04,  0.041, 0.037, 0.048, 0.048, 
0.032, 0.03,  0.032, 0.029, 0.043, 0.056, 0.057, 0.046, 0.034, 0.035, 
0.026,0.036, 0.048, 0.038, 0.032, 0.034, 0.027, 0.024, 0.041, 0.05,  0.056, 
0.038, 0.027, 0.034, 0.027, 0.042, 0.054, 0.054, 0.039, 0.036, 0.029, 
0.027,0.04,  0.052, 0.058, 0.051, 0.028, 0.025, 0.035, 0.037, 0.053, 0.059, 
0.049, 0.044, 0.035, 0.021, 0.044, 0.059, 0.054, 0.052, 0.041, 0.032, 
0.036,0.039, 0.051, 0.056, 0.038, 0.04,  0.022, 0.015, 0.043, 0.054, 0.052, 
0.05,  0.031, 0.03,  0.03,  0.031, 0.044, 0.051, 0.047, 0.04,  0.038, 
0.037,0.06,  0.071, 0.07,  0.066, 0.038, 0.031, 0.045, 0.064, 0.065, 0.074, 
0.08,  0.052, 0.048, 0.041, 0.053, 0.072, 0.079, 0.071, 0.043, 0.059, 0.05, 
0.061, 0.061, 0.055, 0.069, 0.07,  0.057, 0.057, 0.055, 0.074, 0.071, 0.051, 
0.048, 0.05,  0.053, 0.069, 0.086, 0.085, 0.07,  0.047, 0.05,  0.047,0.055, 
0.073, 0.065, 0.056, 0.054, 0.048, 0.043, 0.063, 0.078, 0.087, 0.068, 0.047, 
0.052, 0.048, 0.065, 0.085, 0.084, 0.062, 0.049, 0.05,  0.05, 0.068, 0.084, 
0.095, 0.089, 0.052, 0.052, 0.062, 0.062, 0.086, 0.09,  0.078, 0.062, 0.058, 
0.038, 0.068, 0.095, 0.09,  0.082, 0.069, 0.057, 0.058,0.064, 0.082, 0.087, 
0.055, 0.053, 0.032, 0.033, 0.067, 0.087, 0.087, 0.079, 0.058, 0.053, 0.057, 
0.047, 0.069, 0.085, 0.075, 0.068, 0.063, 0.062,0.076, 0.089, 0.095, 0.086, 
0.056, 0.053, 0.063, 0.082, 0.08,  0.099, 0.101, 0.067, 0.065, 0.058, 0.066, 
0.086, 0.103, 0.088, 0.051, 0.072, 0.06, 0.08,  0.078, 0.067, 0.084, 0.086, 
0.067, 0.066, 0.068, 0.087, 0.087, 0.071, 0.063, 0.065, 0.067, 0.087, 0.104, 
0.108, 0.086, 0.057, 0.063, 0.056,0.064, 0.087, 0.084, 0.07,  0.063, 0.061, 
0.06,  0.076, 0.095, 0.11,  0.088, 0.057, 0.062, 0.067, 0.079, 0.097, 0.105, 
0.079, 0.055, 0.064, 0.066,0.087, 0.104, 0.12,  0.113, 0.063, 0.07,  0.075, 
0.073, 0.104, 0.111, 0.091, 0.072, 0.07,  0.05,  0.083, 0.114, 0.11,  0.098, 
0.083, 0.077, 0.07, 0.078, 0.098, 0.105, 0.069, 0.062, 0.045, 0.046, 0.083, 
0.106, 0.106, 0.093, 0.077, 0.075, 0.073, 0.057, 0.088, 0.105, 0.094, 0.084, 
0.082, 0.081)

x <- c(1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  
10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10,13, 16, 19, 1,  
4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 
19, 1,  4,  7,  10, 13, 16, 19, 1, 4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 
13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  
7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 
1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4, 7,  10, 13, 
16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  
10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  
4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 
19, 1,  4,  7, 10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 
13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19,1,  4,  
7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 
1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10,13, 16, 19, 1,  4,  7,  10, 13, 
16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  4,  7,  
10, 13, 16, 19, 1, 4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19, 1,  
4,  7,  10, 13, 16, 19, 1,  4,  7,  10, 13, 16, 19)

y  <- c(0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1,0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1,  0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 
0.1, 0.1, 0.1, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2,0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3,0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.3, 0.3, 0.3)

wireframe(z ~ x * y, xlab="Parameter 1", ylab="Parameter 2", zlab="Fitness Value")

Using plotly I would like to do something similar, but it always says that z needs to be a matrix. And I don't understand how this maps to x and y.

library(plotly)
p <- plot_ly(x = x, y = y, z = z) %>% add_surface()
p

Even better would be a data.table example, because my data is actually in a data.table where z is a column, x and y are columns, and there are a large number of other parameter columns that will be used for plots.

df.ex <- data.table(Output=z,Input1=x,Input2=y,Input3=rnorm(315),Input4 = 
abs(rnorm(315)+.5))

wireframe(df.ex$Output ~ df.ex$Input1 * df.ex$Input2)

Recollection

I don't know plotly, but fyi, data.table supports syntax like df.ex[, wireframe(Output ~ Input1 * Input2)], that is, you can skip the $. – Durston

Answer 1

Something like this works well. Is this what you want?

library(plotly)
data <- data.frame(x=x,y=y,z=z)
plot_ly() %>% 
  add_trace(data = data,  x=data$x, y=data$y, z=data$z, type="mesh3d" ) 

Fraught

This works well! What is the difference between the add_surface() and add_trace()? I had a similar problem to OP, as I also though add_surface() was the way to go. – Keenakeenan

Is there a way to do this with out the weird flat surfaces at the edge of the data range? ie in the image above there is a darker triangle between the top of the hump and the top right-most data point. This is not part of the actual data but mesh3d adds it for some reason. – Tantalous

Great answer @Edgar Santos! I am curious to try the same thing with my data. Can you please take a look at this question if you have time? #65997174 thank you! – Gummous

Answer 2

See this discussion on Github, what Plotly surface triangulation can do and cannot do: https://github.com/plotly/plotly.py/issues/2194#issuecomment-586917671

Briefly, the issue is the 3D Delauney triangulation that is done with the plotly default parameters, when no i,j,k coordinates and no value for alphahull is given.

In order, to plot the 3D surface as actual 3D surface without additional faces resulting from 3D Delauney triangulation you need to do the following:

1. Project your points onto the xy plane and triangulate the resulting 2d points via scipy.spatial.Delaunay in python for example. In R you can use delaunayn I think. This package interfaces the same package as scipy.spatial
2. Then, you lift the triangulation to 3d space See the example at https://plot.ly/~empet/15527 and the detailed explanation of what plotly 3D surface is capable of directly in the linked github issue.

Peritonitis