Creating a polar histogram

Question

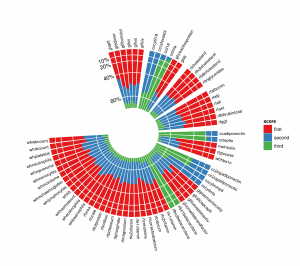
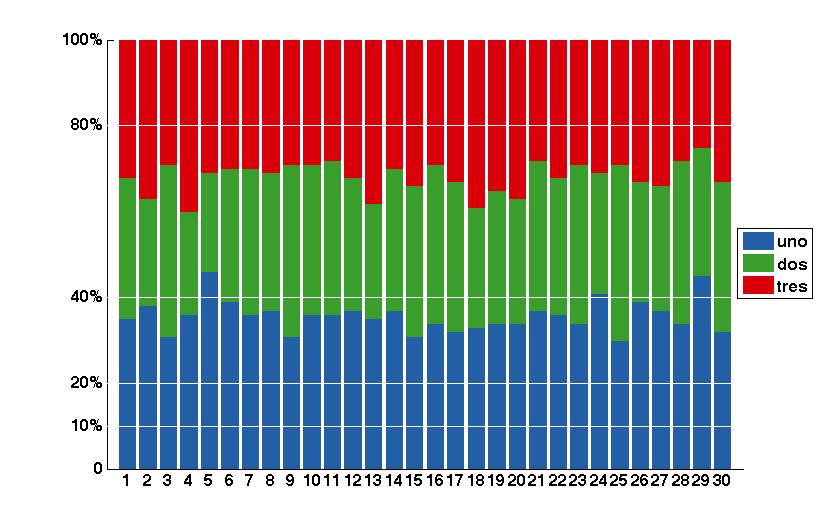
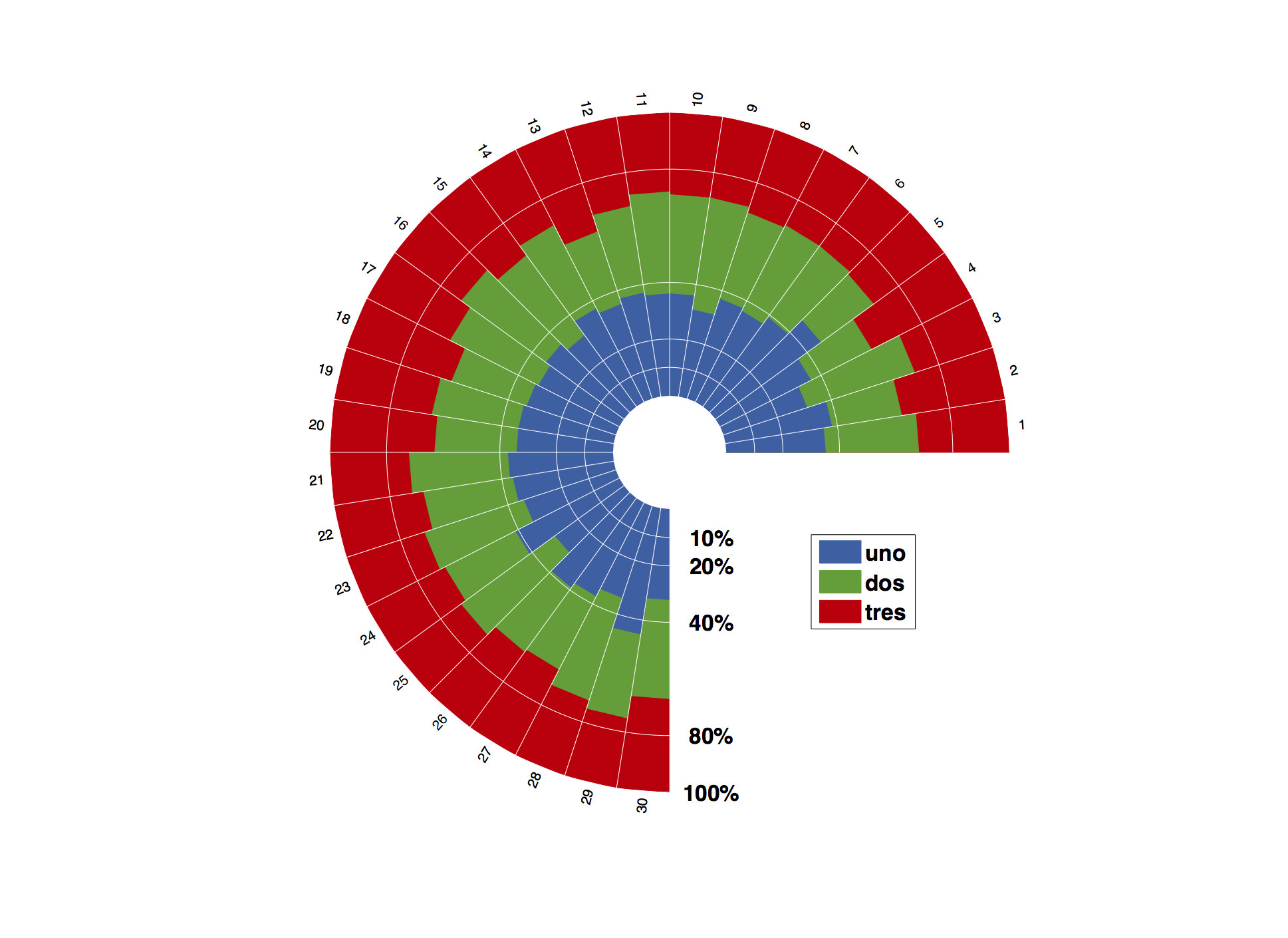
Polar histograms can be very useful for plotting stacked bar graph with multiple entries. An example is provided in the image below of the figure target. This can be made somehow easily in R with ggplot2. Similar function as 'rose' in matlab doesn't seem to allow such a result.

As a starting point, here is what I have:

• Script

% inputs
l = [1 1.4 2 5 1 5 10;
      10 5 1 5 2 1.4 1;
      5 6 3 1 3 2 4];
alpha = [10 20 50 30 25 60 50]; % in degrees
label = 1:length(alpha);

% setings
offset = 1;
alpha_gap = 2;

polarHist(l,alpha,label)

• Function polarHist

function polarHist(data,alpha,theta_label,offset,alpha_gap,ticks)

if nargin  360-alpha_gap*length(alpha)
    error('Covers more than 360°')
end

% code
theta_right = 90 - alpha_gap + cumsum(-alpha) - alpha_gap*[0:length(alpha)-1];
theta_left = theta_right + alpha;

col = get(gca,'colororder');

for j = 1:size(data,1)
    hold all
    if j == 1
        rho_in = kron(offset*ones(1,length(alpha)),[1 1]);
    else
        rho_in = rho_ext;
    end
    rho_ext = rho_in + kron(data(j,:),[1 1]);
    for k = 1:size(data,2)
        h = makewedge(rho_in(k),rho_ext(k),theta_left(k),theta_right(k),col(j,:));
        if j == size(data,1) && ~isempty(theta_label)
            theta = theta_right(k) + (theta_left(k) - theta_right(k))/2;
            rho = rho_ext(k)+1;
            [x,y] = pol2cart(theta/180*pi,rho);
            lab = text(x,y,num2str(theta_label(k),'%0.f'),'HorizontalAlignment','center','VerticalAlignment','bottom');
            set(lab, 'rotation', theta-90)
        end
    end
end
axis equal
theta = linspace(pi/2,min(theta_right)/180*pi);
%ticks = [0 5 10 15 20];
rho_ticks = offset + ticks;
ax = polar([ones(length(ticks(2:end)),1)*theta]',[rho_ticks(2:end)'*ones(1,length(theta))]');
set(ax,'color','w','linewidth',1.5)
axis off
for i=1:length(ticks)
    [x,y] = pol2cart((90)/180*pi,rho_ticks(i));
    text(x,y,num2str(ticks(i)),'HorizontalAlignment','right');
end

• Function makewedge

function hOut = makewedge(rho1, rho2, theta1, theta2, color)
%MAKEWEDGE Plot a wedge.
% MAKEWEDGE(rho1, rho2, theta1, theta2, color) plots a polar
% wedge bounded by the given inputs. The angles are in degrees.
%
% h = MAKEWEDGE(...) returns the patch handle.

ang = linspace(theta1/180*pi, theta2/180*pi);
[arc1.x, arc1.y] = pol2cart(ang, rho1);
[arc2.x, arc2.y] = pol2cart(ang, rho2);
x = [arc1.x arc2.x(end:-1:1)];
y = [arc1.y arc2.y(end:-1:1)];
newplot;
h = patch(x, y, color);
if ~ishold
    axis equal tight;
end
if nargout > 0
     hOut = h;
end

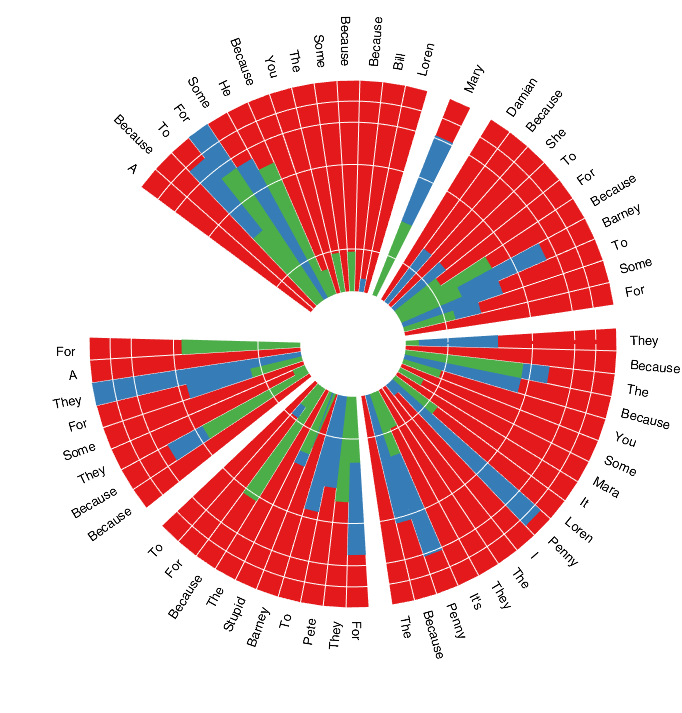
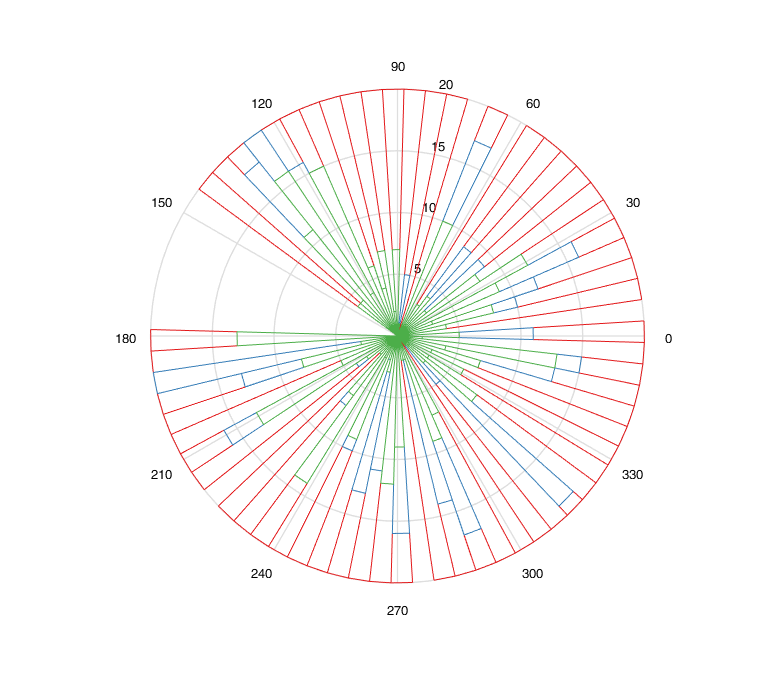
The result is still far from the output of ggplot2 but I think this is a start. I'm struggling to add legend (rows of l)...

Byng

Why can't you do this with multiple rose plots? – Attorney

@Attorney feel free to propose an answer. – Byng

Have you tried that? – Attorney

And please provide sample data so that others can play around and suggest a solution that suits you. – Dorrisdorry

if nargin 360-alpha_gap*length(alpha) ?? dont think that works ! – Westering

Answer 1

This seemed like an interesting problem, so I gave it a go. The code may need some tweaking (as described at the bottom), but you can get a general idea on how to plot something like this. As you'll see, I'm indirectly using Suever's suggestion regarding the rose plots.

I'm not sure when I can find time to perfect this, so if anybody wants to help improve this, let me know and I'll open a Github repo.

function q38054152
%% Define resolution:
W = 5;  % the step size in degrees, larger value = smaller resolution
P = 20; % the "radius" of the external disc (corresponds to the 100%)
%% Generate some data:
M = (1:W:360).';
T = deg2rad(M);
N = numel(M);
S = cell(N,1); for x=1:N,S{x}=feval(@(x)x(1),strsplit(evalc('why')));end
% add some empty regions
M([randi(N,1,5) 30:36]) = NaN;
S(isnan(M)) = cell(1,sum(isnan(M)));
%% Ensure R >= B >= G:
% Generate histogram inputs:
cR = P*ones(N,1); % baseline is fully red
cB = randi(P+1,N,1)-1;
cG = randi(P+1,N,1)-1;
% Replicate:
R = deg2rad(repelem(M, min( cR       ,[],2)));
B = deg2rad(repelem(M, min([cR,cB]   ,[],2)));
G = deg2rad(repelem(M, min([cR,cB,cG],[],2)));
clear cR cB cG
%% Plot:
figure();
hR(1) = rose(R,T); hR(1).Color = [227 025 027]./255; hold on;
hR(2) = rose(B,T); hR(2).Color = [054 125 183]./255;
hR(3) = rose(G,T); hR(3).Color = [076 174 073]./255;
%% Fun with plot:
figure('Color',[1 1 1]); 
% Convert lines to polygons:
patch('XData', hR(1).XData,'YData', hR(1).YData, 'FaceColor', hR(1).Color, 'EdgeColor', 'w');
axis square; axis off; box off; hold on;
patch('XData', hR(2).XData,'YData', hR(2).YData, 'FaceColor', hR(2).Color, 'EdgeColor', 'none');
patch('XData', hR(3).XData,'YData', hR(3).YData, 'FaceColor', hR(3).Color, 'EdgeColor', 'none');
% Remove center (method 1: mask with patch)
xC = cosd(1:360); yC = sind(1:360);
patch('XData', 0.2*P*xC,'YData', 0.2*P*yC, 'FaceColor', [1 1 1], 'EdgeColor', 'none');
% Remove center (method 2: relocate RGB patches using cart2pol and adjusting the inner R)
 % Todo
% Draw "grid":
F = 0.2+0.8*(100-[10 20 40 80])/100;
for ind = 1:numel(F)
  line(xC*F(ind)*P,yC*F(ind)*P,'Color',[1 1 1],'LineWidth',0.1);
end
% Add annotations:
for ind = 1:numel(M)
  if isnan(M(ind))
    continue
  end
  text(xC(M(ind))*P*1.05,yC(M(ind))*P*1.05,S{ind},'Rotation', mod(M(ind)+90,180)-90,...
    'HorizontalAlignment',iftr(M(ind) < 90 || M(ind) > 270,'left','right'));
end

function out = iftr(cond,in1,in2)
%IFTR is a ternary operator implementation
% note: unlike "&&" and "||" this function does not have lazy evaluation capabilities, 
% thus both inputs need to be known before this function executes.
if cond
    out = in1;
else
    out = in2;
end

Results in:

Intermediately we also get this:

Known bugs/issues:

1. The patch objects that are extracted from line objects sometimes create edges where there should be none, resulting in a some strange shapes in the plot (this happens the majority of the time with randomly-generated data, run it and you'll see what I mean).
2. The values of R/G/B need to be scaled, just like the gridlines are scaled, to account for the white circle in the center that takes up 20% of the radius.
3. The white rings' grid needs to be annotated (i.e. "20%", "40%" etc.). Some intelligent way should be found where to place them so the interfere with data as little as possible.
4. Some code is replicated instead of being placed in a function.
5. The legend is missing.

Accouter

So not only will MATLAB cook you dinner, itt will also bring you flowers. Nice work! – Decastro

Nice answer, however the biggest drawback with rose is that the "wedges" top boundary is perpendicular to the rho axis only at the center (not an arc). – Byng

@Byng You have to admit that it's a bit difficult to spot this detail in the image you posted :) I can think of a couple of ways to "fix" this: 1) increase the resolution of the grid by replicating each entry into an odd number of occurrences (so 1 "bar" becomes 3 or 5 or 7 copies of the same), then make sure you fill the label list with NaNs for all but the middle items (so if 1 bar became 3, the labels of the 1st and 3rd will be NaN and the 2nd will be the original). 2) Find the XData,YData of the "arc" segments and add intermediate points to get a "circle" effect. – Accouter

@Accouter Indeed this was already present in the code I gave as a start in the makewedge function... – Byng

Answer 2

You can simplify your problem by using hist to get the accumulated bins for each element, then normalize it to percentage and plot it as polar stacked bars by using patches.

For example lets say your data consist of 30 elements with 1000 samples each, and each sample can be 1,2 or 3.

data=randi(3,1000,30); %create random data

[data_bins,~]=hist(data',3); %Get the accumulated bins

data_bins=data_bins/1000; %Normalize values to percentages

You can plot normal stacked bars to visualize the data

function stackedbar(ymatrix1)

% Create figure
figure1 = figure('Color',[1 1 1]);

% Create axes
axes1 = axes('Parent',figure1,...
    'YTickLabel',{'0','10%','20%','40%','80%','100%'},...
    'YTick',[0 10 20 40 80 100],...
    'XTick',[1:length(ymatrix1)],...
    'FontWeight','bold',...
    'FontSize',16);

xlim(axes1,[0 length(ymatrix1)+1]);
ylim(axes1,[0 100]);

hold(axes1,'all');

% Create multiple lines using matrix input to bar
bar1 = bar(ymatrix1,'EdgeColor',[1 1 1],'BarLayout','stacked',...
    'Parent',axes1);
set(bar1(1),...
    'FaceColor',[0.137254908680916 0.372549027204514 0.647058844566345],...
    'EdgeColor',[0.137254908680916 0.372549027204514 0.647058844566345],...
    'DisplayName','uno');
set(bar1(2),...
    'FaceColor',[0.223529413342476 0.619607865810394 0.168627455830574],...
    'EdgeColor',[0.223529413342476 0.619607865810394 0.168627455830574],...
    'DisplayName','dos');
set(bar1(3),'FaceColor',[0.850980401039124 0 0.0431372560560703],...
    'EdgeColor',[0.850980401039124 0 0.0431372560560703],...
    'DisplayName','tres');

% Create legend
legend1 = legend(axes1,'show');
set(legend1,...
    'Position',[0.902123631386861 0.416961133287318 0.0826277372262772 0.16808336774016]);


plot([0,length(ymatrix1)],[10,10],'w')
plot([0,length(ymatrix1)],[20,20],'w')
plot([0,length(ymatrix1)],[40,40],'w')
plot([0,length(ymatrix1)],[80,80],'w')

You can use same values as polar coordinates by using pol2cart, and by drawing all same color bars in one patch, you can call legend on those patches

function polarstackedbar(data,offset)

% Data is the normalized values and offset is the size of the white circle at the center

yticks=[10,20,40,80,100];

% Create figure
figure1 = figure('Color',[1 1 1]);

% Create axes
axes1 = axes('Parent',figure1,'ZColor',[1 1 1],'YColor',[1 1 1],...
    'XColor',[1 1 1],...
    'PlotBoxAspectRatio',[434 342.3 2.282],...
    'FontWeight','bold',...
    'FontSize',16,...
    'DataAspectRatio',[1 1 1]);

temp=[data(:,1)+data(:,2)+data(:,3)+offset,data(:,1)+data(:,2)+data(:,3)+offset,zeros(length(data),1)]';
temp=temp(:);
temp=[0;temp];

temp2=[data(:,1)+data(:,2)+offset,data(:,1)+data(:,2)+offset,zeros(length(data),1)]';
temp2=temp2(:);
temp2=[0;temp2];

temp3=[data(:,1)+offset,data(:,1)+offset,zeros(length(data),1)]';
temp3=temp3(:);
temp3=[0;temp3];

th=(1:length(data))*3*pi/(2*length(data));
themp=[th;th;th];
themp=themp(:);
themp=[0;0;themp];
themp(end)=[];

% Create patch
[XData1,YData1]=pol2cart(themp,temp);
p1=patch('Parent',axes1,'YData',YData1,...
    'XData',XData1,...
    'FaceColor',[0.850980401039124 0 0.0431372560560703],...
    'EdgeColor',[0.850980401039124 0 0.0431372560560703],...
    'DisplayName','tres');

% Create patch
[XData2,YData2]=pol2cart(themp,temp2);
p2=patch('Parent',axes1,'YData',YData2,...
    'XData',XData2,...
    'FaceColor',[0.223529413342476 0.619607865810394 0.168627455830574],...
    'EdgeColor',[0.223529413342476 0.619607865810394 0.168627455830574],...
    'DisplayName','dos');

% Create patch
[XData3,YData3]=pol2cart(themp,temp3);
p3=patch('Parent',axes1,'YData',YData3,...
    'XData',XData3,...
    'FaceColor',[0.137254908680916 0.372549027204514 0.647058844566345],...
    'EdgeColor',[0.137254908680916 0.372549027204514 0.647058844566345],...
    'DisplayName','uno');

% Create patch
[XData4,YData4]=pol2cart(themp,offset*ones(3*length(data)+1,1));
patch('Parent',axes1,'YData',YData4,...
    'XData',XData4,...
    'LineStyle','none',...
    'FaceColor',[1 1 1]);

% Create legend
legend([p3,p2,p1]);
hold
% Create labels
for i=1:length(data)
    [x,y]=pol2cart((i-0.5)*3*pi/(2*length(data)),offset+5+100);
    h=text(x,y,num2str(i),'HorizontalAlignment','center');
    set(h,'rotation',rad2deg((i-0.5)*3*pi/(2*length(data)))-90+90*sign(cos((i-0.5)*3*pi/(2*length(data)))));

    [x,y]=pol2cart((i)*3*pi/(2*length(data)),offset+15+100);
    plot([0,x],[0,y],'w');
end

thetas=0:0.01:2*pi;

for tick=yticks
    [X,Y]=pol2cart(thetas,tick+offset*ones(1,629));
    plot(X,Y,'w')
    text(X(472)+15,Y(472),strcat(int2str(tick),'%'),'FontWeight','bold','FontSize',16,'HorizontalAlignment','center');
end

Azazel