Very interesting question. I wanted to implement this into mine 4D rendering engine as I was curious how would it look like but I was too lazy and incompetent to handle ND transcendent problems from the math side.
Instead I come up with different solution to this problem. Its not a Fibonaci Latice !!! Instead I expand the parametrical equation of a hypersphere or n-sphere into hyperspiral and then just fit the spiral parameters so the points are more or less equidistant.
It sounds horrible I know but its not that hard and the results look correct to me (finally :) after solving some silly typos copy/paste bugs)
The main idea is to use the n-dimensional parametrical equations for hypersphere to compute its surface points from angles and radius. Here implementation:
see the [edit2]. Now the problem boils down to 2 main problems:
compute number of screws
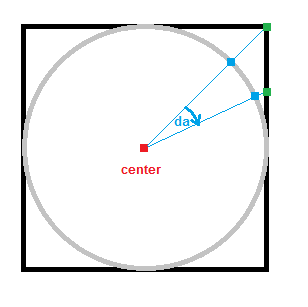
so if we want that our points are equidistant so they must lye on the spiral path in equidistances (see bullet #2) but also the screws itself should have the same distance between each other. For that we can exploit geometrical properties of the hypersphere. Let start with 2D:
![2D spiral]()
so simply screws = r/d. The number of points can be also inferred as points = area/d^2 = PI*r^2/d^2.
so we can simply write 2D spiral as:
t = <0.0,1.0>
a = 2.0*M_PI*screws*t;
x = r*t*cos(a);
y = r*t*sin(a);
To be more simple we can assume r=1.0 so d=d/r (and just scale the points later). Then the expansions (each dimension just adds angle parameter) look like this:
2D:
screws=1.0/d; // radius/d
points=M_PI/(d*d); // surface_area/d^2
a = 2.0*M_PI*t*screws;
x = t*cos(a);
y = t*sin(a);
3D:
screws=M_PI/d; // half_circumference/d
points=4.0*M_PI/(d*d); // surface_area/d^2
a= M_PI*t;
b=2.0*M_PI*t*screws;
x=cos(a) ;
y=sin(a)*cos(b);
z=sin(a)*sin(b);
4D:
screws = M_PI/d;
points = 3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
a= M_PI*t;
b= M_PI*t*screws;
c=2.0*M_PI*t*screws*screws;
x=cos(a) ;
y=sin(a)*cos(b) ;
z=sin(a)*sin(b)*cos(c);
w=sin(a)*sin(b)*sin(c);
Now beware points for 4D are just my assumption. I empirically found out that they relate to constant/d^3 but not exactly. The screws are different for each angle. Mine assumption is that there is no other scale than screws^i but it might need some constant tweaking (did not do analysis of the resulting point-cloud as the result look ok to me)
Now we can generate any point on spiral from single parameter t=<0.0,1.0>.
Note if you reverse the equation so d=f(points) you can have points as input value but beware its just approximate number of points not exact !!!
generate step on spirals so points are equidistant
This is the part I skip the algebraic mess and use fitting instead. I simply binary search delta t so the resulting point is d distant to previous point. So simply generate point t=0 and then binary search t near estimated position until is d distant to the start point. Then repeat this until t<=1.0 ...
You can use binary search or what ever. I know its not as fast as O(1) algebraic approach but no need to derive the stuff for each dimension... Looks 10 iterations are enough for fitting so its not that slow either.
Here implementation from my 4D engine C++/GL/VCL:
void ND_mesh::set_HyperSpiral(int N,double r,double d)
{
int i,j;
reset(N);
d/=r; // unit hyper-sphere
double dd=d*d; // d^2
if (n==2)
{
// r=1,d=!,screws=?
// S = PI*r^2
// screws = r/d
// points = S/d^2
int i0,i;
double a,da,t,dt,dtt;
double x,y,x0,y0;
double screws=1.0/d;
double points=M_PI/(d*d);
dbg=points;
da=2.0*M_PI*screws;
x0=0.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
x=(t*cos(a))-x0; x*=x;
y=(t*sin(a))-y0; y*=y;
if ((!j)&&(x+y<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y>dd) t-=dtt;
}
if (t>1.0) break;
a=da*t;
x0=t*cos(a); pnt.add(x0);
y0=t*sin(a); pnt.add(y0);
as2(i0,i);
}
}
if (n==3)
{
// r=1,d=!,screws=?
// S = 4*PI*r^2
// screws = 2*PI*r/(2*d)
// points = S/d^2
int i0,i;
double a,b,da,db,t,dt,dtt;
double x,y,z,x0,y0,z0;
double screws=M_PI/d;
double points=4.0*M_PI/(d*d);
dbg=points;
da= M_PI;
db=2.0*M_PI*screws;
x0=1.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
z0=0.0; pnt.add(z0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
b=db*t;
x=cos(a) -x0; x*=x;
y=sin(a)*cos(b)-y0; y*=y;
z=sin(a)*sin(b)-z0; z*=z;
if ((!j)&&(x+y+z<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y+z>dd) t-=dtt;
}
if (t>1.0) break;
a=da*t;
b=db*t;
x0=cos(a) ; pnt.add(x0);
y0=sin(a)*cos(b); pnt.add(y0);
z0=sin(a)*sin(b); pnt.add(z0);
as2(i0,i);
}
}
if (n==4)
{
// r=1,d=!,screws=?
// S = 2*PI^2*r^3
// screws = 2*PI*r/(2*d)
// points = 3*PI^3/(4*d^3);
int i0,i;
double a,b,c,da,db,dc,t,dt,dtt;
double x,y,z,w,x0,y0,z0,w0;
double screws = M_PI/d;
double points=3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
dbg=points;
da= M_PI;
db= M_PI*screws;
dc=2.0*M_PI*screws*screws;
x0=1.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
z0=0.0; pnt.add(z0);
w0=0.0; pnt.add(w0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
b=db*t;
c=dc*t;
x=cos(a) -x0; x*=x;
y=sin(a)*cos(b) -y0; y*=y;
z=sin(a)*sin(b)*cos(c)-z0; z*=z;
w=sin(a)*sin(b)*sin(c)-w0; w*=w;
if ((!j)&&(x+y+z+w<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y+z+w>dd) t-=dtt;
} dt=dtt;
if (t>1.0) break;
a=da*t;
b=db*t;
c=dc*t;
x0=cos(a) ; pnt.add(x0);
y0=sin(a)*cos(b) ; pnt.add(y0);
z0=sin(a)*sin(b)*cos(c); pnt.add(z0);
w0=sin(a)*sin(b)*sin(c); pnt.add(w0);
as2(i0,i);
}
}
for (i=0;i<pnt.num;i++) pnt.dat[i]*=r;
for (i=0;i<s1.num;i++) s1.dat[i]*=n;
for (i=0;i<s2.num;i++) s2.dat[i]*=n;
for (i=0;i<s3.num;i++) s3.dat[i]*=n;
for (i=0;i<s4.num;i++) s4.dat[i]*=n;
}
Where n=N are set dimensionality, r is radius and d is desired distance between points. I am using a lot of stuff not declared here but what isimportant is just that pnt[] list the list of points of the object and as2(i0,i1) adds line from points at indexes i0,i1 to the mesh.
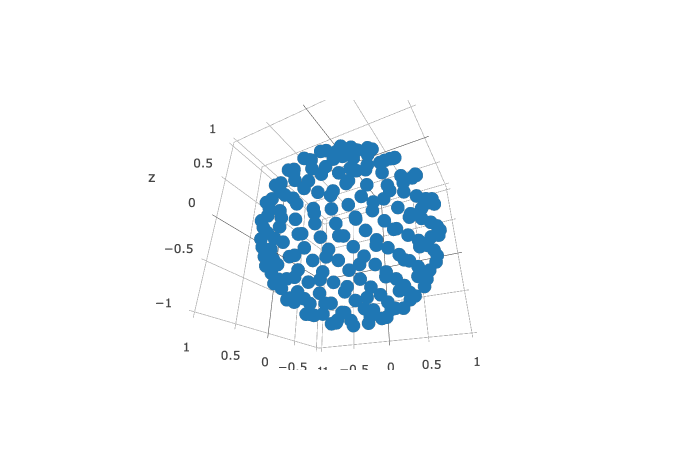
Here few screenshots...
3D perspective:
![3D perspective]()
4D perspective:
![4D perspective]()
4D cross-section with hyperplane w=0.0:
![4D cross-section w=0.0]()
and the same with more points and bigger radius:
![4D cross-section w=0.0 HQ]()
the shape changes with rotations in which its animated ...
[Edit1] more code/info
This is how my engine mesh class look like:
//---------------------------------------------------------------------------
//--- ND Mesh: ver 1.001 ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _ND_mesh_h
#define _ND_mesh_h
//---------------------------------------------------------------------------
#include "list.h" // my dynamic list you can use std::vector<> instead
#include "nd_reper.h" // this is just 5x5 transform matrix
//---------------------------------------------------------------------------
enum _render_enum
{
_render_Wireframe=0,
_render_Polygon,
_render_enums
};
const AnsiString _render_txt[]=
{
"Wireframe",
"Polygon"
};
enum _view_enum
{
_view_Orthographic=0,
_view_Perspective,
_view_CrossSection,
_view_enums
};
const AnsiString _view_txt[]=
{
"Orthographic",
"Perspective",
"Cross section"
};
struct dim_reduction
{
int view; // _view_enum
double coordinate; // cross section hyperplane coordinate or camera focal point looking in W+ direction
double focal_length;
dim_reduction() { view=_view_Perspective; coordinate=-3.5; focal_length=2.0; }
dim_reduction(dim_reduction& a) { *this=a; }
~dim_reduction() {}
dim_reduction* operator = (const dim_reduction *a) { *this=*a; return this; }
//dim_reduction* operator = (const dim_reduction &a) { ...copy... return this; }
};
//---------------------------------------------------------------------------
class ND_mesh
{
public:
int n; // dimensions
List<double> pnt; // ND points (x0,x1,x2,x3,...x(n-1))
List<int> s1; // ND points (i0)
List<int> s2; // ND wireframe (i0,i1)
List<int> s3; // ND triangles (i0,i1,i2,)
List<int> s4; // ND tetrahedrons (i0,i1,i2,i3)
DWORD col; // object color 0x00BBGGRR
int dbg; // debug/test variable
ND_mesh() { reset(0); }
ND_mesh(ND_mesh& a) { *this=a; }
~ND_mesh() {}
ND_mesh* operator = (const ND_mesh *a) { *this=*a; return this; }
//ND_mesh* operator = (const ND_mesh &a) { ...copy... return this; }
// add simplex
void as1(int a0) { s1.add(a0); }
void as2(int a0,int a1) { s2.add(a0); s2.add(a1); }
void as3(int a0,int a1,int a2) { s3.add(a0); s3.add(a1); s3.add(a2); }
void as4(int a0,int a1,int a2,int a3){ s4.add(a0); s4.add(a1); s4.add(a2); s4.add(a3); }
// init ND mesh
void reset(int N);
void set_HyperTetrahedron(int N,double a); // dimensions, side
void set_HyperCube (int N,double a); // dimensions, side
void set_HyperSphere (int N,double r,int points); // dimensions, radius, points per axis
void set_HyperSpiral (int N,double r,double d); // dimensions, radius, distance between points
// render
void glDraw(ND_reper &rep,dim_reduction *cfg,int render); // render mesh
};
//---------------------------------------------------------------------------
#define _cube(a0,a1,a2,a3,a4,a5,a6,a7) { as4(a1,a2,a4,a7); as4(a0,a1,a2,a4); as4(a2,a4,a6,a7); as4(a1,a2,a3,a7); as4(a1,a4,a5,a7); }
//---------------------------------------------------------------------------
void ND_mesh::reset(int N)
{
dbg=0;
if (N>=0) n=N;
pnt.num=0;
s1.num=0;
s2.num=0;
s3.num=0;
s4.num=0;
col=0x00AAAAAA;
}
//---------------------------------------------------------------------------
void ND_mesh::set_HyperSpiral(int N,double r,double d)
{
int i,j;
reset(N);
d/=r; // unit hyper-sphere
double dd=d*d; // d^2
if (n==2)
{
// r=1,d=!,screws=?
// S = PI*r^2
// screws = r/d
// points = S/d^2
int i0,i;
double a,da,t,dt,dtt;
double x,y,x0,y0;
double screws=1.0/d;
double points=M_PI/(d*d);
dbg=points;
da=2.0*M_PI*screws;
x0=0.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
x=(t*cos(a))-x0; x*=x;
y=(t*sin(a))-y0; y*=y;
if ((!j)&&(x+y<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y>dd) t-=dtt;
}
if (t>1.0) break;
a=da*t;
x0=t*cos(a); pnt.add(x0);
y0=t*sin(a); pnt.add(y0);
as2(i0,i);
}
}
if (n==3)
{
// r=1,d=!,screws=?
// S = 4*PI*r^2
// screws = 2*PI*r/(2*d)
// points = S/d^2
int i0,i;
double a,b,da,db,t,dt,dtt;
double x,y,z,x0,y0,z0;
double screws=M_PI/d;
double points=4.0*M_PI/(d*d);
dbg=points;
da= M_PI;
db=2.0*M_PI*screws;
x0=1.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
z0=0.0; pnt.add(z0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
b=db*t;
x=cos(a) -x0; x*=x;
y=sin(a)*cos(b)-y0; y*=y;
z=sin(a)*sin(b)-z0; z*=z;
if ((!j)&&(x+y+z<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y+z>dd) t-=dtt;
}
if (t>1.0) break;
a=da*t;
b=db*t;
x0=cos(a) ; pnt.add(x0);
y0=sin(a)*cos(b); pnt.add(y0);
z0=sin(a)*sin(b); pnt.add(z0);
as2(i0,i);
}
}
if (n==4)
{
// r=1,d=!,screws=?
// S = 2*PI^2*r^3
// screws = 2*PI*r/(2*d)
// points = 3*PI^3/(4*d^3);
int i0,i;
double a,b,c,da,db,dc,t,dt,dtt;
double x,y,z,w,x0,y0,z0,w0;
double screws = M_PI/d;
double points=3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
dbg=points;
da= M_PI;
db= M_PI*screws;
dc=2.0*M_PI*screws*screws;
x0=1.0; pnt.add(x0);
y0=0.0; pnt.add(y0);
z0=0.0; pnt.add(z0);
w0=0.0; pnt.add(w0);
dt=0.1*(1.0/points);
for (t=0.0,i0=0,i=1;;i0=i,i++)
{
for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
{
t+=dtt;
a=da*t;
b=db*t;
c=dc*t;
x=cos(a) -x0; x*=x;
y=sin(a)*cos(b) -y0; y*=y;
z=sin(a)*sin(b)*cos(c)-z0; z*=z;
w=sin(a)*sin(b)*sin(c)-w0; w*=w;
if ((!j)&&(x+y+z+w<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
if (x+y+z+w>dd) t-=dtt;
} dt=dtt;
if (t>1.0) break;
a=da*t;
b=db*t;
c=dc*t;
x0=cos(a) ; pnt.add(x0);
y0=sin(a)*cos(b) ; pnt.add(y0);
z0=sin(a)*sin(b)*cos(c); pnt.add(z0);
w0=sin(a)*sin(b)*sin(c); pnt.add(w0);
as2(i0,i);
}
}
for (i=0;i<pnt.num;i++) pnt.dat[i]*=r;
for (i=0;i<s1.num;i++) s1.dat[i]*=n;
for (i=0;i<s2.num;i++) s2.dat[i]*=n;
for (i=0;i<s3.num;i++) s3.dat[i]*=n;
for (i=0;i<s4.num;i++) s4.dat[i]*=n;
}
//---------------------------------------------------------------------------
void ND_mesh::glDraw(ND_reper &rep,dim_reduction *cfg,int render)
{
int N,i,j,i0,i1,i2,i3;
const int n0=0,n1=n,n2=n+n,n3=n2+n,n4=n3+n;
double a,b,w,F,*p0,*p1,*p2,*p3,_zero=1e-6;
vector<4> v;
List<double> tmp,t0; // temp
List<double> S1,S2,S3,S4; // reduced simplexes
#define _swap(aa,bb) { double *p=aa.dat; aa.dat=bb.dat; bb.dat=p; int q=aa.siz; aa.siz=bb.siz; bb.siz=q; q=aa.num; aa.num=bb.num; bb.num=q; }
// apply transform matrix pnt -> tmp
tmp.allocate(pnt.num); tmp.num=pnt.num;
for (i=0;i<pnt.num;i+=n)
{
v.ld(0.0,0.0,0.0,0.0);
for (j=0;j<n;j++) v.a[j]=pnt.dat[i+j];
rep.l2g(v,v);
for (j=0;j<n;j++) tmp.dat[i+j]=v.a[j];
}
// copy simplexes and convert point indexes to points (only due to cross section)
S1.allocate(s1.num*n); S1.num=0; for (i=0;i<s1.num;i++) for (j=0;j<n;j++) S1.add(tmp.dat[s1.dat[i]+j]);
S2.allocate(s2.num*n); S2.num=0; for (i=0;i<s2.num;i++) for (j=0;j<n;j++) S2.add(tmp.dat[s2.dat[i]+j]);
S3.allocate(s3.num*n); S3.num=0; for (i=0;i<s3.num;i++) for (j=0;j<n;j++) S3.add(tmp.dat[s3.dat[i]+j]);
S4.allocate(s4.num*n); S4.num=0; for (i=0;i<s4.num;i++) for (j=0;j<n;j++) S4.add(tmp.dat[s4.dat[i]+j]);
// reduce dimensions
for (N=n;N>2;)
{
N--;
if (cfg[N].view==_view_Orthographic){} // no change
if (cfg[N].view==_view_Perspective)
{
w=cfg[N].coordinate;
F=cfg[N].focal_length;
for (i=0;i<S1.num;i+=n)
{
a=S1.dat[i+N]-w;
if (a>=F) a=F/a; else a=0.0;
for (j=0;j<n;j++) S1.dat[i+j]*=a;
}
for (i=0;i<S2.num;i+=n)
{
a=S2.dat[i+N]-w;
if (a>=F) a=F/a; else a=0.0;
for (j=0;j<n;j++) S2.dat[i+j]*=a;
}
for (i=0;i<S3.num;i+=n)
{
a=S3.dat[i+N]-w;
if (a>=F) a=F/a; else a=0.0;
for (j=0;j<n;j++) S3.dat[i+j]*=a;
}
for (i=0;i<S4.num;i+=n)
{
a=S4.dat[i+N]-w;
if (a>=F) a=F/a; else a=0.0;
for (j=0;j<n;j++) S4.dat[i+j]*=a;
}
}
if (cfg[N].view==_view_CrossSection)
{
w=cfg[N].coordinate;
_swap(S1,tmp); for (S1.num=0,i=0;i<tmp.num;i+=n1) // points
{
p0=tmp.dat+i+n0;
if (fabs(p0[N]-w)<=_zero)
{
for (j=0;j<n;j++) S1.add(p0[j]);
}
}
_swap(S2,tmp); for (S2.num=0,i=0;i<tmp.num;i+=n2) // lines
{
p0=tmp.dat+i+n0; a=p0[N]; b=p0[N];// a=min,b=max
p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
if (fabs(a-w)+fabs(b-w)<=_zero) // fully inside
{
for (j=0;j<n;j++) S2.add(p0[j]);
for (j=0;j<n;j++) S2.add(p1[j]);
continue;
}
if ((a<=w)&&(b>=w)) // intersection -> points
{
a=(w-p0[N])/(p1[N]-p0[N]);
for (j=0;j<n;j++) S1.add(p0[j]+a*(p1[j]-p0[j]));
}
}
_swap(S3,tmp); for (S3.num=0,i=0;i<tmp.num;i+=n3) // triangles
{
p0=tmp.dat+i+n0; a=p0[N]; b=p0[N];// a=min,b=max
p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
p2=tmp.dat+i+n2; if (a>p2[N]) a=p2[N]; if (b<p2[N]) b=p2[N];
if (fabs(a-w)+fabs(b-w)<=_zero) // fully inside
{
for (j=0;j<n;j++) S3.add(p0[j]);
for (j=0;j<n;j++) S3.add(p1[j]);
for (j=0;j<n;j++) S3.add(p2[j]);
continue;
}
if ((a<=w)&&(b>=w)) // cross section -> t0
{
t0.num=0;
i0=0; if (p0[N]<w-_zero) i0=1; if (p0[N]>w+_zero) i0=2;
i1=0; if (p1[N]<w-_zero) i1=1; if (p1[N]>w+_zero) i1=2;
i2=0; if (p2[N]<w-_zero) i2=1; if (p2[N]>w+_zero) i2=2;
if (i0+i1==3){ a=(w-p0[N])/(p1[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p1[j]-p0[j])); }
if (i1+i2==3){ a=(w-p1[N])/(p2[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p2[j]-p1[j])); }
if (i2+i0==3){ a=(w-p2[N])/(p0[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p0[j]-p2[j])); }
if (!i0) for (j=0;j<n;j++) t0.add(p0[j]);
if (!i1) for (j=0;j<n;j++) t0.add(p1[j]);
if (!i2) for (j=0;j<n;j++) t0.add(p2[j]);
if (t0.num==n1) for (j=0;j<t0.num;j++) S1.add(t0.dat[j]);// copy t0 to target simplex based on points count
if (t0.num==n2) for (j=0;j<t0.num;j++) S2.add(t0.dat[j]);
if (t0.num==n3) for (j=0;j<t0.num;j++) S3.add(t0.dat[j]);
}
}
_swap(S4,tmp); for (S4.num=0,i=0;i<tmp.num;i+=n4) // tetrahedrons
{
p0=tmp.dat+i+n0; a=p0[N]; b=p0[N];// a=min,b=max
p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
p2=tmp.dat+i+n2; if (a>p2[N]) a=p2[N]; if (b<p2[N]) b=p2[N];
p3=tmp.dat+i+n3; if (a>p3[N]) a=p3[N]; if (b<p3[N]) b=p3[N];
if (fabs(a-w)+fabs(b-w)<=_zero) // fully inside
{
for (j=0;j<n;j++) S4.add(p0[j]);
for (j=0;j<n;j++) S4.add(p1[j]);
for (j=0;j<n;j++) S4.add(p2[j]);
for (j=0;j<n;j++) S4.add(p3[j]);
continue;
}
if ((a<=w)&&(b>=w)) // cross section -> t0
{
t0.num=0;
i0=0; if (p0[N]<w-_zero) i0=1; if (p0[N]>w+_zero) i0=2;
i1=0; if (p1[N]<w-_zero) i1=1; if (p1[N]>w+_zero) i1=2;
i2=0; if (p2[N]<w-_zero) i2=1; if (p2[N]>w+_zero) i2=2;
i3=0; if (p3[N]<w-_zero) i3=1; if (p3[N]>w+_zero) i3=2;
if (i0+i1==3){ a=(w-p0[N])/(p1[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p1[j]-p0[j])); }
if (i1+i2==3){ a=(w-p1[N])/(p2[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p2[j]-p1[j])); }
if (i2+i0==3){ a=(w-p2[N])/(p0[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p0[j]-p2[j])); }
if (i0+i3==3){ a=(w-p0[N])/(p3[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p3[j]-p0[j])); }
if (i1+i3==3){ a=(w-p1[N])/(p3[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p3[j]-p1[j])); }
if (i2+i3==3){ a=(w-p2[N])/(p3[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p3[j]-p2[j])); }
if (!i0) for (j=0;j<n;j++) t0.add(p0[j]);
if (!i1) for (j=0;j<n;j++) t0.add(p1[j]);
if (!i2) for (j=0;j<n;j++) t0.add(p2[j]);
if (!i3) for (j=0;j<n;j++) t0.add(p3[j]);
if (t0.num==n1) for (j=0;j<t0.num;j++) S1.add(t0.dat[j]);// copy t0 to target simplex based on points count
if (t0.num==n2) for (j=0;j<t0.num;j++) S2.add(t0.dat[j]);
if (t0.num==n3) for (j=0;j<t0.num;j++) S3.add(t0.dat[j]);
if (t0.num==n4) for (j=0;j<t0.num;j++) S4.add(t0.dat[j]);
}
}
}
}
glColor4ubv((BYTE*)(&col));
if (render==_render_Wireframe)
{
// add points from higher primitives
for (i=0;i<S2.num;i++) S1.add(S2.dat[i]);
for (i=0;i<S3.num;i++) S1.add(S3.dat[i]);
for (i=0;i<S4.num;i++) S1.add(S4.dat[i]);
glPointSize(5.0);
glBegin(GL_POINTS);
glNormal3d(0.0,0.0,1.0);
if (n==2) for (i=0;i<S1.num;i+=n1) glVertex2dv(S1.dat+i);
if (n>=3) for (i=0;i<S1.num;i+=n1) glVertex3dv(S1.dat+i);
glEnd();
glPointSize(1.0);
glBegin(GL_LINES);
glNormal3d(0.0,0.0,1.0);
if (n==2)
{
for (i=0;i<S2.num;i+=n1) glVertex2dv(S2.dat+i);
for (i=0;i<S3.num;i+=n3)
{
glVertex2dv(S3.dat+i+n0); glVertex2dv(S3.dat+i+n1);
glVertex2dv(S3.dat+i+n1); glVertex2dv(S3.dat+i+n2);
glVertex2dv(S3.dat+i+n2); glVertex2dv(S3.dat+i+n0);
}
for (i=0;i<S4.num;i+=n4)
{
glVertex2dv(S4.dat+i+n0); glVertex2dv(S4.dat+i+n1);
glVertex2dv(S4.dat+i+n1); glVertex2dv(S4.dat+i+n2);
glVertex2dv(S4.dat+i+n2); glVertex2dv(S4.dat+i+n0);
glVertex2dv(S4.dat+i+n0); glVertex2dv(S4.dat+i+n3);
glVertex2dv(S4.dat+i+n1); glVertex2dv(S4.dat+i+n3);
glVertex2dv(S4.dat+i+n2); glVertex2dv(S4.dat+i+n3);
}
}
if (n>=3)
{
for (i=0;i<S2.num;i+=n1) glVertex3dv(S2.dat+i);
for (i=0;i<S3.num;i+=n3)
{
glVertex3dv(S3.dat+i+n0); glVertex3dv(S3.dat+i+n1);
glVertex3dv(S3.dat+i+n1); glVertex3dv(S3.dat+i+n2);
glVertex3dv(S3.dat+i+n2); glVertex3dv(S3.dat+i+n0);
}
for (i=0;i<S4.num;i+=n4)
{
glVertex3dv(S4.dat+i+n0); glVertex3dv(S4.dat+i+n1);
glVertex3dv(S4.dat+i+n1); glVertex3dv(S4.dat+i+n2);
glVertex3dv(S4.dat+i+n2); glVertex3dv(S4.dat+i+n0);
glVertex3dv(S4.dat+i+n0); glVertex3dv(S4.dat+i+n3);
glVertex3dv(S4.dat+i+n1); glVertex3dv(S4.dat+i+n3);
glVertex3dv(S4.dat+i+n2); glVertex3dv(S4.dat+i+n3);
}
}
glEnd();
}
if (render==_render_Polygon)
{
double nor[3],a[3],b[3],q;
#define _triangle2(ss,p0,p1,p2) \
{ \
glVertex2dv(ss.dat+i+p0); \
glVertex2dv(ss.dat+i+p1); \
glVertex2dv(ss.dat+i+p2); \
}
#define _triangle3(ss,p0,p1,p2) \
{ \
for(j=0;(j<3)&&(j<n);j++) \
{ \
a[j]=ss.dat[i+p1+j]-ss.dat[i+p0+j]; \
b[j]=ss.dat[i+p2+j]-ss.dat[i+p1+j]; \
} \
for(;j<3;j++){ a[j]=0.0; b[j]=0.0; } \
nor[0]=(a[1]*b[2])-(a[2]*b[1]); \
nor[1]=(a[2]*b[0])-(a[0]*b[2]); \
nor[2]=(a[0]*b[1])-(a[1]*b[0]); \
q=sqrt((nor[0]*nor[0])+(nor[1]*nor[1])+(nor[2]*nor[2])); \
if (q>1e-10) q=1.0/q; else q-0.0; \
for (j=0;j<3;j++) nor[j]*=q; \
glNormal3dv(nor); \
glVertex3dv(ss.dat+i+p0); \
glVertex3dv(ss.dat+i+p1); \
glVertex3dv(ss.dat+i+p2); \
}
#define _triangle3b(ss,p0,p1,p2) \
{ \
glNormal3dv(nor3.dat+(i/n)); \
glVertex3dv(ss.dat+i+p0); \
glVertex3dv(ss.dat+i+p1); \
glVertex3dv(ss.dat+i+p2); \
}
glBegin(GL_TRIANGLES);
if (n==2)
{
glNormal3d(0.0,0.0,1.0);
for (i=0;i<S3.num;i+=n3) _triangle2(S3,n0,n1,n2);
for (i=0;i<S4.num;i+=n4)
{
_triangle2(S4,n0,n1,n2);
_triangle2(S4,n3,n0,n1);
_triangle2(S4,n3,n1,n2);
_triangle2(S4,n3,n2,n0);
}
}
if (n>=3)
{
for (i=0;i<S3.num;i+=n3) _triangle3 (S3,n0,n1,n2);
for (i=0;i<S4.num;i+=n4)
{
_triangle3(S4,n0,n1,n2);
_triangle3(S4,n3,n0,n1);
_triangle3(S4,n3,n1,n2);
_triangle3(S4,n3,n2,n0);
}
glNormal3d(0.0,0.0,1.0);
}
glEnd();
#undef _triangle2
#undef _triangle3
}
#undef _swap
}
//---------------------------------------------------------------------------
#undef _cube
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------
I use mine dynamic list template so:
List<double> xxx; is the same as double xxx[];
xxx.add(5); adds 5 to end of the list
xxx[7] access array element (safe)
xxx.dat[7] access array element (unsafe but fast direct access)
xxx.num is the actual used size of the array
xxx.reset() clears the array and set xxx.num=0
xxx.allocate(100) preallocate space for 100 items
so you need to port it to any list you have at disposal (like std:vector<>). I also use 5x5 transform matrix where
void ND_reper::g2l (vector<4> &l,vector<4> &g); // global xyzw -> local xyzw
void ND_reper::l2g (vector<4> &g,vector<4> &l); // global xyzw <- local xyzw
convert point either to global or local coordinates (by multiplying direct or inverse matrix by point). You can ignore it as its used just once in the rendering and you can copy the points instead (no rotation)... In the same header are also some constants:
const double pi = M_PI;
const double pi2 =2.0*M_PI;
const double pipol=0.5*M_PI;
const double deg=M_PI/180.0;
const double rad=180.0/M_PI;
I got also vector and matrix math template integrated in the transform matrix header so vector<n> is n dimensional vector and matrix<n> is n*n square matrix but its used only for rendering so again you can ignore it. If youre interested here few links from whic all this was derived:
The enums and dimension reductions are used only for rendering. The cfg holds how should be each dimension reduced down to 2D.
AnsiString is a self relocating string from VCL so either use char* or string class you got in your environment. DWORD is just unsigned 32 bit int. Hope I did not forget something ...













W=0is also spiral like shape in 3D (had some silly typo copy/paste bug in the code). I added answer with mine approximate approach. – Santoninpoints = 1.0/dand compare result with differentdif the ratiopnt.num/pointsis constant you found youconstantifnto try1.0/d^2etc ... for screws I expect just each added angle will have one more*screwin it ... – Santonindif not find out in which direction and change screws for that angle by multiplying a constant until it matches But I dont think that is needed as the angle range after 3D is symmetrical all are<0,M_PI>except last one. Anyway if you found out some interesting ratios / constant I would be happy if you comment them to me so I can update my code also :) – Santoninafor|p(r,0,0,0) - p(r,a,0,0)| = daand that would be the screw angle increment in that angle. Similarly|p(r,0,0,0) - p(r,0,b,0)| = d... from that you can compute screws for each angle separatelyscrewsa=M_PI/a,screwsb=screwsa * M_PI/bscrewsc=screwsa*screwsb*M_PI/a.... only the last one will bescrews? = screwsa*.....*2.0*M_PI/?.... that is how I see it but if it actually works is worth trying Maybe I will try it but don't know when I need to go now – Santonin