How to express tetration function, for complex numbers

Question

There do exists so-called hyperoperation sequence. It works like you construct multiplication a*b=a+a+a+a...+a with many additions of a repeated b times. Then there goes exponentiation a^b = a*a*a*a*...*a with many multiplicaitions of a repeated b times. Then, there goes tetration, expressed as a tower of exponentiations, same like a^^b == a^a^a^...^a , repeated b times.

I am interested how to write this function, for floating point and complex numbers?

I've alredy wrote multiplication and exponentiation functions, in glsl:

// complex multiplication:
vec2 cmul(in vec2 a, in vec2 b) {
    return vec2(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);
}

// complex exponent e^a
vec2 cexp(in vec2 a) {
    float ea = exp(a.x);
    float vl = a.y;
    return ea * vec2( cos(vl), sin(vl) );
}

// complex natural logarithm ln(a)
vec2 cln(in vec2 a) {
    float ql = length(a);
    return vec2( log(ql), atan(a.y, a.x));
}

// complex power function a^b
vec2 cpow(in vec2 a, in vec2 b) {
    return cexp(cmul(cln(a), b));   
}

But then I'm stuck! How can we write ctet(in vec2 a, in vec2 b) tetration function, not only for floating point numbers, but for whole complex plane itself?

Kraut

What an interesting question! From what I'm reading about generalizing tetration to complex powers, it seems like this is decidedly nontrivial and even proving that such a generalization exists was a tough problem to crack. You may want to ask this question more abstractly at math.stackexchange.com, since the folks there might be able to point you at a good solution. – Nicolanicolai

@Nicolanicolai Maybe you're right, because it's not the problem we face every day. Many people havent' ever heard of tetration.. Probably I should ask on math forum first, but they may "throw an integral at me", and this has nothing to do with actual computation algorithm for a program I can write on PC.. – Kraut

@Spektre i had aloot of work on the week, and no spare time to even visit here)). I will read your answer after work, after several hours. – Kraut

@Spectre I want to experiment with this for iterating fractals, like Mandelbrot. So I need continues formula for complex plane, plus on wiki it was stated there's just one such analytic continuation for tetration function. But that's hobby I need to switch brain to it. after work , I hope I will have some time in the evening – Kraut

@Kraut I completely reedited my answer removed old stuff leaving just the final code for both real and complex domain, added some more screenshots of the fractal added some more info clear out unused links and images and deleted obsolete comments ... – Elrod

Answer 1

well lets start with Real domain and integer b only:

a^^b = a^a^a^a^a...^a  // a is there b times

this can be evaluated like this in C++:

double tetration(double a,int b)    // a^^b = a^a^a^a... b times
    {
    double c;
    if (b<=0) return 0;
    for (c=a;b>1;b--) c=pow(a,c);
    return c;
    }

as You already got the pow for complex domain you can do the same there too... To keep this simple I will not touch that for now ...

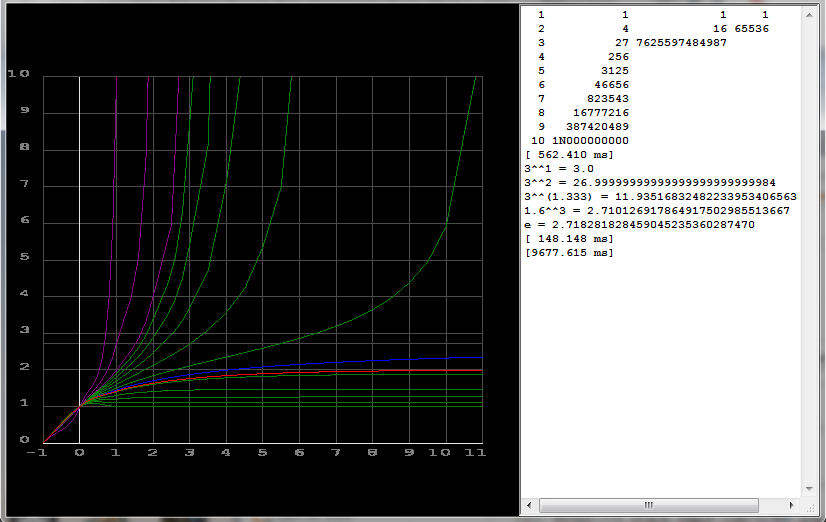
Here some results:

a\b| 1|   2|            3|    4
-------------------------------
 1 | 1|   1|            1|    1
 2 | 2|   4|           16|65536
 3 | 3|  27|7625597484987|
 4 | 4| 256|             |
 5 | 5|3125|             |

btw. all of these hyper operations are related to Ackermann function you can find iterative implementation of mine in C++ in here:

• How was C ported to architectures that had no hardware stack?

However due to extremly fast growth even double will out of range soon (hence missing values)...

Now how to move the b to Real domain? Have not a clue about algebraic approach for this but geometric one is possible.

Simply "plot" a^^b as a function of variable b and constant a for integer values of b around your wanted real b and then interpolate Real domain b using Integer domain b as control points. Its similar to obtaining non integer order derivation of a function.

So (X,Y) will be your (a^^b,b). Now use any interpolation to construct Real domain function.

Linear interpolation will look like this:

y0 = a^^(int(b)) 
y1 = a^^(int(b)+1)
a^^b = y0 + (b-int(b))*(y1-y0)

However higher order interpolation is needed and also the interpolation parameter should be scaled to non linear metrics. For more info see:

• How can i produce multi point linear interpolation?

After some elaboration cubics (t^3) and log^2 scale proved to be sufficient (C++ example using my 128 bit floating point f128 class just rename it to double):

f128 tetration_fi(f128 a,int b)     // a^^b = a^a^a^a... b times
    {
    f128 c;
    if (b==-1) return 0.0;          // first singularity
    if (b== 0) return 1.0;          // second singularity
    if (b< -1) return 0.0;          // uncomputed
    for (c=a;b>1;b--) c=pow(a,c);
    return c;
    }
//---------------------------------------------------------------------------
f128 tetration_ff(f128 a,f128 b)    // a^^b = a^a^a^a... b times
    {
    int bi;
    f128 z0,z1,z2,z3,a0,a1,a2,a3,t,tt,ttt,o=2.0;
    if (b==-1) return 0.0;          // first singularity
    if (b== 0) return 1.0;          // second singularity
    if (b< -1) return 0.0;          // uncomputed
    bi=b.ToInt(); b-=bi;
    if (b.iszero()) return tetration_fi(a,bi);

    z0=tetration_fi(a,bi-1);        // known points around a^^b
    z1=pow(a,z0);
    z2=pow(a,z1);
    z3=pow(a,z2);

    z0=log2(log2(z0+o)+o);          // log^2 scale
    z1=log2(log2(z1+o)+o);
    z2=log2(log2(z2+o)+o);
    z3=log2(log2(z2+o)+o);

    t =0.5*(z2-z0);                 // cubic interpolation coeff.
    tt=0.5*(z3-z1);
    a0=z1;
    a1=t;
    a2=(3.0*(z2-z1))-(2.0*t)-tt;
    a3=t+tt+(2.0*(z1-z2));

    t=b-bi;                         // cubic interpolation
    tt=t*t;
    ttt=tt*t;
    z0=a0+(a1*t)+(a2*t*t)+(a3*t*t*t);

    z0=exp2(exp2(z0)-o)-o;          // linear scale
    return z0;
    }
//---------------------------------------------------------------------------

This is what I compared it with:

• Tetration

I select the same graph bases a from a^^b and as you can see its a very good match only range below 1.0 is slightly off.

Lets go for the Complex domain fractal

Now when you want to go to complex domain you can not do the same as in Real because the results are too chaotic for interpolation. So we can only stick to integer b or use the Kneser algorithm to compute.

Luckily for us there are more ways on show the fractal... For example we can evaluate integer b from the a^^b where only the a is complex and use the result for coloring the output. Here GLSL example (based on mine Mandelbrot shader and your complex math):

Fragment:

// Fragment
#version 450 core
uniform dvec2 p0=dvec2(0.0,0.0);        // mouse position <-1,+1>
uniform double zoom=1.000;          // zoom [-]
in smooth vec2 p32;
out vec4 col;
//---------------------------------------------------------------------------
// All components are in the range [0…1], including hue.
vec3 rgb2hsv(vec3 c)
    {
    vec4 K = vec4(0.0, -1.0 / 3.0, 2.0 / 3.0, -1.0);
    vec4 p = mix(vec4(c.bg, K.wz), vec4(c.gb, K.xy), step(c.b, c.g));
    vec4 q = mix(vec4(p.xyw, c.r), vec4(c.r, p.yzx), step(p.x, c.r));
    float d = q.x - min(q.w, q.y);
    float e = 1.0e-10;
    return vec3(abs(q.z + (q.w - q.y) / (6.0 * d + e)), d / (q.x + e), q.x);
    }
//---------------------------------------------------------------------------
// All components are in the range [0…1], including hue.
vec3 hsv2rgb(vec3 c)
    {
    vec4 K = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
    vec3 p = abs(fract(c.xxx + K.xyz) * 6.0 - K.www);
    return c.z * mix(K.xxx, clamp(p - K.xxx, 0.0, 1.0), c.y);
    }
//---------------------------------------------------------------------------
vec3 spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  vec3 c=vec3(0.0,0.0,0.0);
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); c.r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); c.r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); c.r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); c.r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); c.r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); c.g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); c.g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); c.g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); c.b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); c.b=0.7 -(     t)+(0.30*t*t); }
    return c;
    }
//---------------------------------------------------------------------------
// complex domain math
vec3 color_wheel(vec2 a)    // complex -> polar -> HSV -> RGB
    {
    float an=(atan(-a.y,-a.x)*0.15915494309189533576888376337251)+0.5;
    float  r=length(a); r-=floor(r); r*=0.75; r+=0.25;
    return hsv2rgb(vec3(an,1.0,r));
    }
vec3 color_spectral(vec2 a) // complex -> wavelength -> RGB
    {
    float  r=length(a); r-=floor(r);
    return spectral_color(400.0+(300.0*r));
    }
vec2 cadd(vec2 a,vec2 b)    // a+b
    {
    return a+b;
    }
vec2 csub(vec2 a,vec2 b)    // a-b
    {
    return a-b;
    }
vec2 cmul(vec2 a,vec2 b)    // a*b
    {
    return vec2((a.x*b.x)-(a.y*b.y),(a.x*b.y)+(a.y*b.x));
    }
vec2 cdiv(vec2 a,vec2 b)    // a/b
    {
    float an=atan(-a.y,-a.x)-atan(-b.y,-b.x);
    float  r=length(a)/length(b);
    return r*vec2(cos(an),sin(an));
    }
vec2 csqr(vec2 a)           // a^2
    {
    return cmul(a,a);
    }
vec2 cexp(vec2 a)           // e^a
    {
//  e^(x+y*i)= e^x * e^(y*i) = e^x * ( cos(y) + i*sin(y) )
    return exp(a.x)*vec2(cos(a.y),sin(a.y));
    }
vec2 cln(vec2 a)            // ln(a)
    {
    return vec2(log(length(a)),atan(a.y,a.x));
    }
vec2 cpow(vec2 a,vec2 b)    // a^b
    {
    return cexp(cmul(cln(a),b));
    }
vec2 ctet(vec2 a,int b)     // a^^b
    {
    vec2 c=vec2(1.0,0.0);
    for (;b>0;b--) c=cpow(a,c);
    return c;
    }
//---------------------------------------------------------------------------
void main()
    {
    // poistion (double)
    dvec2 p=dvec2(p32);
    p=(p/zoom)-p0;          // x,y (-1.0, 1.0)
    // position (float)
    vec2 pp=vec2(p);

    // [chose function]

    // complex domain test function 1 (color wheel)
//  vec2 a=cdiv(cmul(csub(cmul(pp,pp),vec2(1.0,0.0)),csqr(csub(pp,vec2(2.0,1.0)))),cadd(csqr(pp),vec2(2.0,2.0)));
    // complex domain test function 2 (color wheel)
//  vec2 a=pp; a=cln(a);
    // exponentiation escape fractal 1 (color wheel)
//  vec2 a=cpow(pp,vec2(100,0));
    // exponentiation escape fractal 2 (color wheel)
//  vec2 a=vec2(1.0,1.0); for (int i=0;i<100;i++) a=cpow(a,pp);
    // exponentiation escape fractal 3 (color wheel)
//  vec2 a=vec2(0.0,0.0),b=vec2(1.0,0.0); float r=0.5,rr=1.0,wt=0.1; for (int i=0;i<20;i++){ a+=rr*cexp(vec2(-b.y,b.x)*wt); b=cmul(b,pp); rr*=r; } a*=(1.0-r);
    // tetration escape fractal (grayscale)
//  vec2 a=ctet(pp,100);
    // pentation escape fractal (grayscale)
    vec2 a=pp; for (int i=0;i<20;i++) a=ctet(a,20); a*=100.0;
                                                   
    // [chose coloring method]

    // grayscale based on escape
    float r=0.2*length(a); r-=floor(r); r=0.25+0.75*r; col=vec4(r,r,r,1.0);
    // RGB based on result
//  col=vec4(a,a.x+a.y,1.0);
    // result -> wavelength+intensity
//  col=vec4(color_wheel(a),1.0);
    // result -> spectral color
//  col=vec4(color_spectral(a),1.0);
    }

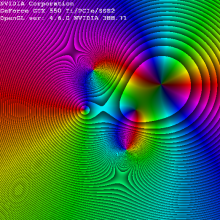
And tetration preview:

This is what I compared with:

• power tower (tetration) fractal

and it matches my result is just mirrored in both x,y

So what I did was computing a^^100 where a is complex domain position of fragment on screen <-1,+1> with some panning and zooming and render the color constructed from the result ...

I leave there also a test function (not fractal) I used to test the coloring methods and complex math taken from here the first is from Wiki the second is shader result (color wheel):

You can do escape testing like for mandelbrot or whatever else algo to show the fractal instead.

Here coloring options screenshots of tetration (I like the grayscale) of zoom=500.0 pos=-0.188418+0.234466i

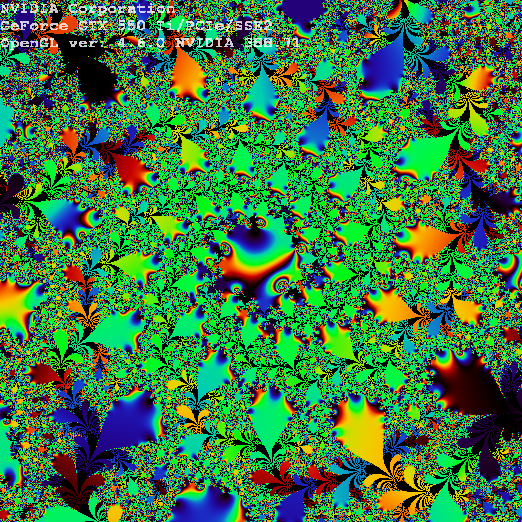
And finally pentation:

Elrod

I have looked, and have a comment. I think that linear interpolation will go for lower-order linear operations. But for tetration is non-linear(i mean non-elementary) function, so its not by linear interpolation y=c+(d-c)*((x-a)/(b-a)). Maybe this require exponential interpolation y=c*(d/c)^((x-a)/(b-a))? – Kraut

I think that for complex plane, and iterative fractals need to stick Kneser tetration solution. Anyway, thanks for your input and some reference points. Lets wait a bit more, maybe there would be other ideas :^) – Kraut

@Kraut looks like no need for Kneser ... its so simple and fast just single for cycle with single cpow in it ... :) – Elrod

Nope, its not desired "iterated tetration" fractal, but "iterated exponentiation" fractal. Classic mandelbrot squaring fractal goes z=z^2+ c. Let's call it order 1. Next order 2 is exponentiation fractal:. Z = c * e^z. That is what we did.. Now I want to go ORDER 3: z = ctet(something, z), maybe raised to power C... How can we built tetration fractal? how to get precise ctet(artg,towrHeight) for small Z? – Kraut

Nah, you not get the point. Take classic mandel. Z^2+C. Its what I call "order 1". Its base step is multiplication. But when iterated it becomes exponentiation. Order 2. Is C*e^Z. That is base formula that You did. Repeated it gives tetration, indeed – Kraut

Order 3. Repeat ctet(2.0, Z)^C inside loop. That was never implemented iterated, it would give pentation.. Now you get?)) We need ctet tetration fractal. What you did is exp fractal, not tetration(despite exp iterated gives tetration, I call fractal by its base step formula) – Kraut

In my terminology I want repeated tet() fractal, so asked for function ctet(base, height). In your terminology I want to see pentation fractal.. – Kraut

I think that we do see horisontal stripes due to limited precision and overflow.. But ctet function for a complex arg.. How do you do it?!... Oh maaan... Do a=ctet(2.0, a); That Is the challenge!!! – Kraut

That is pentation fractal that not built yet. Sometimes 2 tetrated to complex Z would overflow, sometimes will orbit. But how to tetrate real number to complex height!? That's challenge and we haven't seen that fractal yet – Kraut

@Kraut then the knesser is the only known way but can not find any nice equations or explanations on it. Everywhere I look is just a comment they use some calculator that computes it ... btw the horizontal stripes are not there all the time ... in some cobination of the for loop counts the shape changes and its sort of symmetrical along y axis mirror ... btw tetration fractal has them too they a re the base for the leaf like stuff in there ... – Elrod

Same thing, I can't find.. I've built z=pow(z,smth)+c, with smth=2,3,... classic mandel, then I've built z=c*pow(smth, z), smth=2 or e, and got same result as you. Now wanted tet() fractal and "ran into a wall" :) why you see different? because when you iterate more in single step you may miss sometimes. only iterate one exp() per iteration, your first one was correct! when you iterate 100 times you will loss precision, and got something other. changes you will see will diverge from original to something wrong, when you zoom in... the correct one is with these "lobes" and spirals. – Kraut

@Kraut this is I think what we seek Operational details (Implementation) of Kneser's method of fractional iteration of function exp(x)? but the math notation is not that I am used to and stuff is way above my knowledge It would be probably faster to create own interpolation in complex domain then grasph that one ... – Elrod

Let us continue this discussion in chat. – Kraut

@Kraut I might have an insaine idea of interpolating the tetration complex^^real by analyzing the geometric properties of complex^^integer tetration the result is orbiting some center area (slightly oscillating around it). The geometric motion properties might be detectable from some first integer tetrations so it might be possible to interpolate relatively simply however result would be not exact !!! and might be off slightly due to inaccuracy in center approximation and different scale/metrics of parameter similarly to what I got in Real^^Real. – Elrod

@Kraut the speed and direction of the orbiting is proportional to imaginary part of the base. Sadly the magnitude is matching Real^^Real tetration only for zero imaginary part so no shortcut there ... the oscilation of center is weird looks like mostly dependent on imaginary part of base... When I will have time mood will try to cubic interpolate the motion parameters but have no idea when ... – Elrod

@Kraut btw your deleted "answer" is more suited to post on SO META that is the place to complain about bugs ... so the Devs can repair them ...Go to your profile page and click on the meta user link in top right corner of the page ... – Elrod

Now using browser version, its much more usable than mobile app. I think that app is not needed to be developed. Just removed it, its very poorly developed and has several glitches and is very inconvenient. Chrome version of site is much more better. – Kraut